图论中的概念(3)——同构
图的同构(isomorphism of graphs)
(1)称G=(V,E)及G¢=(V¢,E¢)二图同构,记为G≅G¢Û存在 着两个双射函数j及y,j : V ®V¢ ,y : E®E¢ ,使得
y(u,v)=(u¢,v¢)Þj (u)=u¢Ùj (v)=v¢ (*)
(2)称G=(V,E,g)及G¢=(V¢,E¢,g¢)二图同构,记为G≅G¢Û存在着两个双射函数j及y,j : V ®V¢ ,y : E®E¢ ,使得 y(e)=e¢Ùg(e)={ u,v}Ùg¢(e¢)={ u¢,v¢}Þj(u)=u¢Ùj(v)=v¢
或 y(e)=e¢Ùg(e)=(u,v)Ùg¢(e¢)=(u¢,v¢)Þj (u)=u¢Ùj (v)=v¢
注: ·此定义(1)中(*)式也可改写为:
y(u,v)= (j(u), j(v)) (*¢)
此定义(2)中(**)式也可改写为:
g(e)={ u,v}Þ g¢(y(e))={ j(u), j(v)}
或 g(e)=(u,v)Þ g¢(y(e))=(j(u), j(v))
这实际上就是图的同态公式;
·图的同构远比代数系统的同构复杂。这是因为图的同构在同态公式中牵扯着两个(甚至三个,考虑定义三)双射函数的交叉关系,而代数系统的同构在同态公式中只有一个双射函数。因此图的同构问题不象代数系统的同构问题那样有许多进展、有几个定理好用,迄今为止,没有任何进展,没有任何定理可用,仅仅只能用定义。
例1.
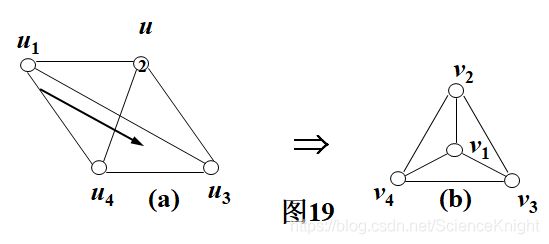
图19中的(a)和(b)二无向图是同构的。
(采用变形法)其同构函数为j及y ,使得
j (u1)=v1 , j (u2)=v2 , j (u3)=v3 , j (u4)=v4 ;
y(u1,u2)=(v1, v2) , y(u1,u3)=(v1, v3) , y(u1,u4)=(v1, v4) ,
y(u2,u3)=(v2, v3) ,y(u2,u4)=(v1, v2) , y(u3,u4)=(v3, v4);
从而j及y是两个双射函数,且满足同态公式(*),因此(a)和(b)二图是同构的。
例2
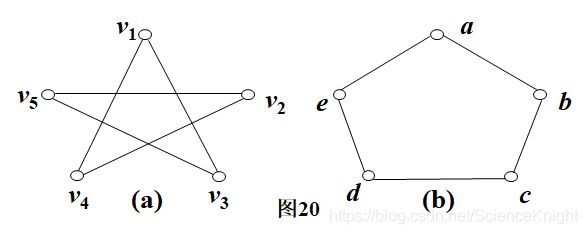
图20中的(a)和(b)二无向图是同构的。
(采用抻路蹦圈法)其同构函数为j及y ,使得
j(v1)=a, j(v2)=c, j(v3)=e, j(v4)=b, j(v5)=d ;
y(v1,v3)=(a, e) , y(v1,v4)=(a, b) , y(v2,v4)=(c, b) ,
y(v2,v5)=(c, d) ,y(v3,v5)=(e, d) ;
从而j及y是两个双射函数,且满足同态公式(*),因此(a)和(b)二图是同构的。
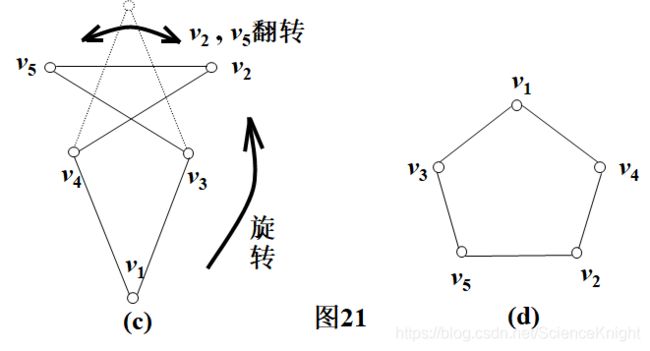
两个图能否同构,从直观的意义上讲是能否将其中的一个图示通过某些“变形”后使它成为另一个图示的形状。如将(a)图示作如下变形-蹦圈后就可得到(b)图示:
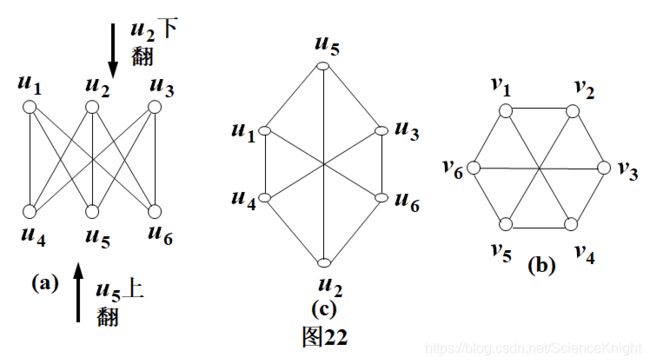
例3.图22中的(a)和(b)二无向图是同构的。
(采用抻路蹦圈法)其同构函数为j及y,使得
j(u1)=v1, j(u2)=v5, j(u3)=v3,
j(u4)=v6, j(u5)= v2, j(u6)= v4;
y(u1,u4)=(v1,v6) , y(u1,u5)=(v1,v2) , y(u1,u6)=(v1,v4) ,
y(u2,u4)=(v5,v6) , y(u2,u5)=(v5,v2) , y(u2,u6)=(v5,v4) ,
y(u3,u4)=(v3,v6) , y(u3,u5)=(v3,v2) , y(u3,u6)=(v3,v4) ;
从而j及y是两个双射函数,且满足同态公式(*),因此(a)和(b)二图是同构的。
例4.
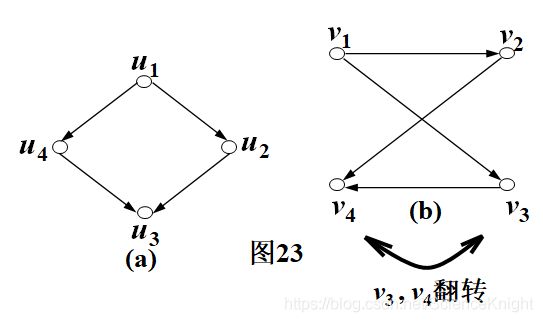
图23中的(a)和(b)二有向图是同构的。
(采用抻路蹦圈法)其同构函数为j及y,使得
j(u1)=v1, j(u2)=v2, j(u3)=v4, j(u4)=v3;
y(u1,u2)=(v1,v2) , y(u1,u4)=(v1,v3) ,
y(u2,u3)=(v2,v4) , y(u4,u3)=(v3,v4) ;
从而j及y是两个双射函数,且满足同态公式(*),因此(a)和(b)二图是同构的。
若两个图同构,则它们必须满足:
(1)结点个数相等;
(2)边数相等;
(3)对应结点的进度、出度、度数均相等;
(4)度数相同的结点个数相等;
(5)平行边对应,重数相等;
(6)自环对应;悬挂点对应;孤立点对应;
(7)结点间的相邻关系对应;边间的相邻关系对应;结点与边的关联关系对应;
(8)圈对应;路对应;
(9)对应圈的长度相等;对应路的长度相等;
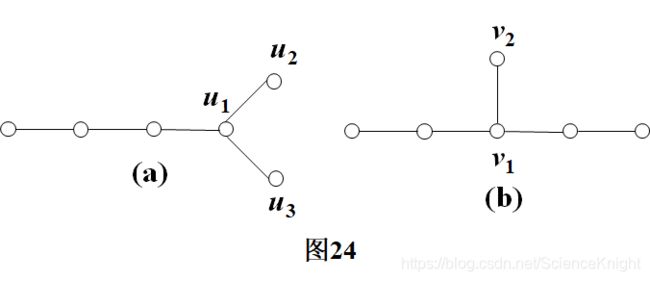
例5.
图24中(a)、(b)两图不同构。
Ulam猜想(1960).
1960年 Ulam提出如下关于图同构的著名猜想,至今无人能够证明或否定。
设G=(V,E)及G¢=(V¢,E¢)是两个图,其结点集分别为
V={ v1, v2, ¼, vn} 及 V¢={ v1¢, v2¢, ¼, vn¢} (n³3) ,则
("iÎN)(1£i£n)(Hi≅ Hi¢) Þ(G ≅ G¢) ,即
若G和G¢ 的n 对特殊真子图对应同构,则G和G¢同构。
这里:Hi =G\{ vi}= (Vi,Ei),
Vi =V\{ vi},
Ei ={(u,v)ú (u,v)ÎEÙ u ¹vi Ù v ¹vi};
Hi¢ =G¢ \{ vi¢}= (Vi¢,Ei¢),
Vi¢ =V¢ \{ vi¢},
Ei¢ ={(u¢,v¢)ú (u¢,v¢)ÎE¢Ùu¢ ¹vi¢Ùv¢ ¹vi¢}。