PyTorch自用笔记（第一周）

一、深度学习初见

1.1 深度学习框架简介

1.1.1 PyTorch的发展

2002年Torch->2011年Torch7
Lua语言制约了Torch发展
PyTorch于2018.12发布正式版本，采用CAFFE2后端
本教程使用的是2019.5发布的1.1

1.1.2 PyTorch与同类框架

Google：theano -> Tensorflow1 -> Tensorflow2 + Keras
Facebook：Torch7 -> Caffe -> PyTorch + Caffe2
Amazon : MXNet
Microsoft : CNTK
Chainer
tensorflow是静态图优先的而PyTorch是动态图优先的

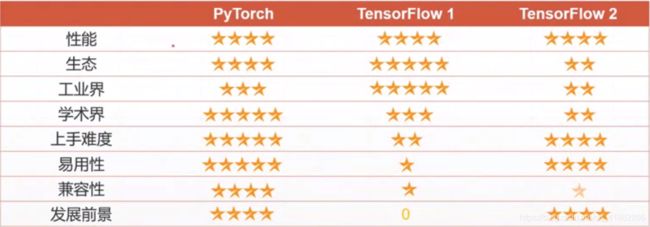
总结：
对于研究员，推荐使用PyTorch
对于工程师，推荐使用TensorFlow2

二、环境配置

Python 3.7 + Anaconda 5.3.1
CUDA 10.0
Pycharm Community

三、回归问题

3.1 简单回归问题

3.1.1 梯度下降法

loss：x² * sin(x)
导数：2xsinx + x²cosx
x^’ = x - α * f^’(x)
α：学习率，控制梯度下降速度，一般设置为0.0001或0.01
由于噪声的存在，loss可以转化为(W * X + b - y)²的形式，当此loss函数取得极小值时，参数W和b即为所求参数

3.1.2 线性回归、逻辑回归、分类问题

线性回归的结果y∈R
逻辑回归由于加了激活函数的限制，将最终结果限制到了[0, 1]中，变为一个概率问题
分类问题特点：每个结果的概率加起来等于1
回归问题实验代码

import numpy as np


def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(points))


def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        w_gradient += -(2 / N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]


def gradient_descent_runner(points, starting_b, startint_w, learning_rate, num_iterations):
    b = starting_b
    w = startint_w
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]


def run():
    points = np.genfromtxt("data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iterations = 1000
    print("Staring gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w,
                  compute_error_for_line_given_points(initial_b, initial_w, points))
          )
    print("Running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After{0} iterations b = {1}, w = {2}, error = {3}".
          format(num_iterations, b, w,
                 compute_error_for_line_given_points(b, w, points))
          )


if __name__ == 'main':
    run()

结果：
Starting gradient descent at b = 0, w = 0, error = 5565.107834483211
Running…
After 1000 iterations b = 0.08893651993741346, w = 1.4777440851894448, error = 112.61481011613473

部分数据：

3.2 分类问题引入

MNIST数据集：0~9手写数字识别
· 每个数字有7k张图片
· 训练集60k，测试集10k
pred结果采用one-hot编码

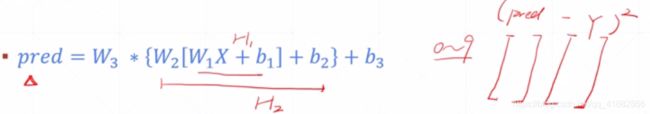
线性相关模型难以解决具有非线性特征的问题，故引入非线性因素激活函数ReLU，然后运用梯度下降法将代价函数最小化，对于每一个新的X（手写数字），送到pred进行前向运算，取概率值最大的label为预测值

手写数字识别

H₁ = relu(XW₁ + b ₁)
H₂ = relu(H₁W₂ + b ₂)
H₁ = f(H₂W₃ + b ₃)
步骤：

1. 加载数据
2. 建立模型
3. 训练
4. 测试