数据库理论：关系代数与 SQL

前言

关系代数通过符号化的语言，来描述数据库的行为关系，相当于简化版的 SQL。比如并，交，差，笛卡尔积，除法，select 语句等等。

SQL 则是结构化查询语句，相比于关系代数，更方便被计算机识别的一种查询语言。

---

其余的复习笔记：

数据库理论：函数式依赖，无损拆分，依赖保留拆分与数据库范式

数据库理论：ER模型，关系转换，并发控制与冲突可串行化调度

关系代数

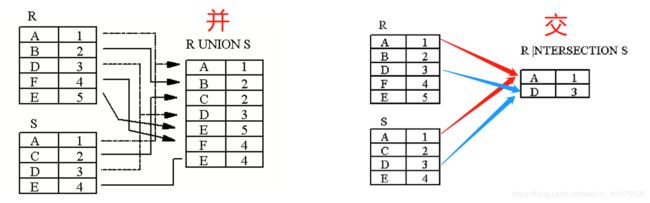
交，并，差，笛卡尔积等符号，和数学上的符号完全一致，只是运算的单位不是集合而是表。

交运算取两张表相同的字段。并运算类似，也是合并相同的字段，同时加入不相同的字段：

差运算则是减去两者的交集。笛卡尔积则组合任意的属性：

选择语句

关系代数中用符号 σ（西格玛，sigma）来描述选择语句。此外我们可以在 select 的同时，添加限制条件（即 where），使用例如下：

$${\sigma }_{选择条件}(数据表名称)$$

比如：
$${\sigma }_{AGE=19}(student)$$

就等价于：

select * from student where AGE=19;

投影语句

在关系代数中的投影语句相当于 SQL 中的字段筛选，可以选择特定的字段进行查询，格式如下：

$${\pi }_{属性}(表名)$$

比如：

$${\pi }_{sno,age,sname}(student)$$

就等价于：

select sno, age, sname from student;

此外，投影语句也可以和选择语句的 where 联动：

$${\pi }_{sname}({\sigma }_{AGE=19}(student))$$

就相当于一个完整的 select 语句：

select sname from student where AGE=19;

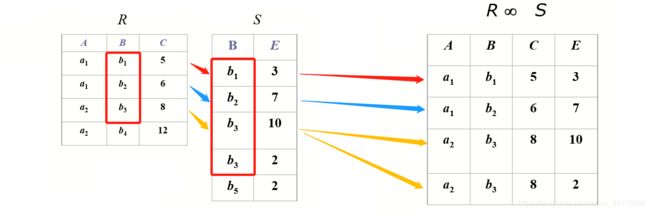
连接语句

关于连接的 SQL 版本，可以看我之前的博客：MySQL 连接（JOIN）使用 简单讲解与示例

关系代数版本的连接语句如下，假设有两张表 R 和 S，通过某些条件把他们进行连接，用 ∞ 号表示连接：

$$R{\infty }_{连接条件}S$$

这相当于先将两张表取笛卡尔积，再根据连接条件从中进行筛选：

$$R{\infty }_{连接条件}S\leftrightarrow {\sigma }_{连接条件}(R\times S)$$

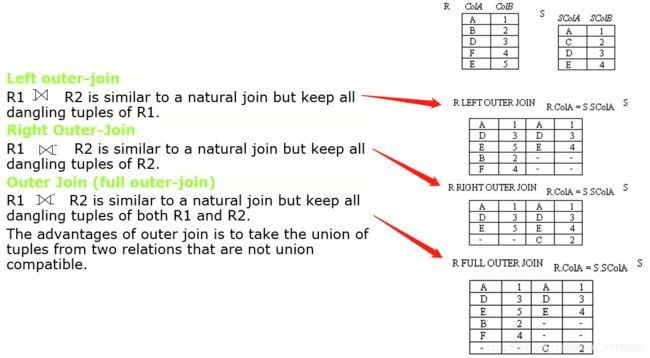
一般连接中都认为连接条件是带有等号的（比如外键），这种连接叫做等号连接。通常可以省略连接条件。能够省略的又称为 “自然连接” （natural join）

外连接则是在内连接的基础上，为无法匹配的记录 添加空行 ：

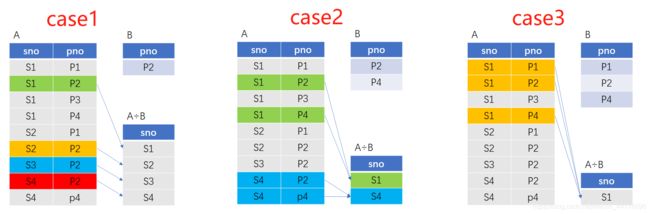
除法（重要⚠）

除法是乘法（笛卡尔积 ）的逆运算，值得注意的是，关系代数中除法只为整除。

只有当除表的所有记录，在被除表中全部命中时，才认为发生了整除。如下图，当 A 表中某几条记录完全被 B 完成命中时，才认为发生整除，其他部分都不算整除。

下图颜色三个除法例子。可以用 A÷B 再 × B，就能得到下图的颜色标记部分：

除法常用作选取带有 ALL 字眼的题目，比如选取选了所有课程的学生，那么用课程表去（course）除选课记录表（SC），就能得有选了所有课程的学生：

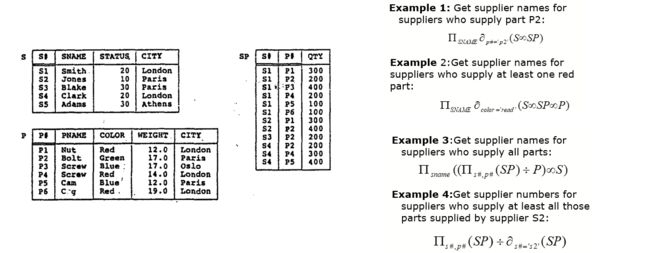
关系代数例题

假设有三张表：

1. 供应商 supplier，S
2. 产品 product，P
3. 购买记录 SP

有如下的四个例题，题干和答案，分析如下：

第一题比较简单，直接连接一次即可。

第二题需要连接两次。第一次连接找出 SP 表中所有 color=red 的记录，第二次连接找出这些记录对应的 supplier 的 sname

第三题先利用 SP÷P 找出所有 supply 了所有 parts（products）的 supplier 的 #S（即 sid），然后再和 S 表连接，找出 sname

第四题题干比较绕，就是找出一些供应商，他们买了所有【供应商 S2 购买的产品】，结合题目的表来看，S2 买了 P1，P2。于是我们要找出所有也同时买了 P1，P2 的供应商。

注：
这里其实我根本没有看懂题干，是通过关系代数表达式反推的题目。。。
不得不吐槽巴斯克桑的英语咖喱味太浓了，或者说我的英语太种花
至今不明白学校为何不用中文 ppt
OTL

SQL

没啥特别的，真不熟

就是提几点比较冷门或者比较难的：

视图

创建视图允许用户访问一个表的部分，方便管理权限，有着管中窥豹的作用。视图可以看作一张 “虚表”。

通过 create 语句可以创建视图，视图的创建基于 select 语句，选择某些属性暴露在外：

模式匹配

通过 LIKE 子句，在 where 中使用 like 来进行模式匹配，进而进行筛选。其中：

1. % 号能够匹配任意字符串，包括空串
2. _ 号能够匹配单个字符

是不是有点像 leetcode 的某一题模式匹配？

聚合，分组与HAVING

聚合函数通常计算某一群记录的聚合值，比如平均数。常用的有：

• COUNT：计数
• AVG：平均
• MAX：极大
• MIN：极小
• SUM：求和

比如计算每个月 A 产品的平均售价：

select AVG(售价) from 数据表
where 产品id=A

那么最终结果只会返回一行，就是均值！

聚合函数会将所有记录都压缩为一条记录。而分组（group by）则允许我们拆分这些聚合的过程，或者说是分组聚合。

比如按照月份分组，计算每个月 A 产品的平均售价，那么有：

select AVG(售价) from 数据表
where 产品id=A
group by month

where 子句在分组（group by）之前进行筛选，而 having 子句则可以在分组之后进行筛选。

还是以上面的例子为拓展，比如按照月份分组，计算每个月 A 产品的平均售价。此外，我们只需要 5 月份以后的数据，那么有：

select AVG(售价) from 数据表
where 产品id=A
group by month
having month>=5

having 的用途就很清晰了。因为聚合函数返回的记录不止一条（比如典型的按月 group by），having 负责在 group by 之后再次筛选结果。

子查询

嵌套的查询。类比于 c 语言的多层 for 循环。子查询返回一条记录，或者几条（那就是集合了）

可以使用 IN，ANY，ALL 等关键字对子查询返回的集合进行判断。

当返回一条记录时，我们可以利用等号来进行判断。比如查询所有和 BOB 一个部门的员工（通过部门 id，deptno 来判断）：

select * from employee
where deptno=(
	select deptno from employee where ename='BOB'
	);

而如果 BOB 不止一个，即子查询返回的是一个集合，那么我们使用 ANY 或者 ALL 来进行判断。

如果有两个 BOB 在不同的部门 A，B 那么我们利用 ANY 子句，只要和任意一个 BOB 在同一个部门，不管是 A 还是 B，我们都选上：

select * from employee
where deptno = ANY (
	select deptno from employee where ename='BOB'
	);

其中 ANY，SOME 都是只要命中一条即可返回 true，而 ALL 要求全部命中，否则返回 false。此外，exist 要求子查询返回的结果不为空集，not exist 则相反。

比如查找所有成绩（gpa，绩点，分数）大于 A01 班级所有人的同学：

select * from student
where gpa > ALL (
	select gpa from student where classNO='A01'
);

当前同学的 gpa 必须大于子查询返回的集合中的任意一个 gpa，否则查询失败。这表示我们通过二重循环进行查询。

外循环枚举每个学生，内循环枚举所有 A01 班的学生，判断，翻译为 std c++ 代码大概长这样：

struct STUDENT
{
     
	std::string sname;
	std::string classNO;
	float gpa;
	...
};

std::vector<STUDENT> student;

for(int i=0; i<student.size(); i++)
{
     
	float gpa = student[i].gpa;
	for(int j=0; j<student.size(); j++)
	{
     
		if(student[j].classNO != "A01") continue;
		if(gpa > student[j].gpa)
			std::cout<<student[i]<<std::endl;	// 满足条件 输出当前学生
	}
}

复杂度 n 方起步。所以子查询是非常消耗性能的，能不用就不用。

SQL 例题

生僻题，不用连接，用子查询。

题①：找出选修全部课程的学生。思路是双重否定。先找出有缺课（即没有选修全部课程）的学生，然后再遍历所有学生，排除那些缺课的学生：

题②：假设学号为 2006002001 的学生选课的集合为 X，找出选修了 X 中所有课程的学生。思路和上一题类似，只是【全部课程】改为了【X 集合中的课程】，思路还是双重否定：

select * from Student s
where not exist (
	select * from course c
	where sid=2006002001
	and not exist (
		select * from sc
		where s.sid=sc.sid
		and c.cid=sc.cid
	));

这里就能体现关系代数的方便。直接一次除法就搞定了，不把那子查询干的碎碎的?