使用遗传算法解旅行商问题

1.问题描述
旅行商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设 有n个城市和距离矩阵D=[dij]，其中dij表示 城市i到城市j的距离，i，j=1，2 … n，则问 题是要找出遍访每个城市恰好一次的一条 回路并使其路径长度为最短。

2.算法设计
旅行商问题是一个十分经典的NP难度问题，如果想找到真正的唯一最优的解复杂度是O(N!)的，所以求解这一类问题的策略就是找一个相对最优的解，也就是最优化问题。模拟进化算法就是一种组合优算法，通过模拟生物遗传进化过程来找到最优的种族，也就是TSP中的最短路径。

在这里，我把一条路径作为遗传算法的基因，初始基因序列就是初始路径，最后进化后的得到的基因序列就是找到的最短的路径。把待优化问题的目标函数理解成某生物种群对环境的适应性问题。
本文算法流程图如下所示：

在产生后代时，若既定概率大于交叉概率，则认为这个父样本是强父样本，直接保留下来。交叉时选择父样本1的前半段，然后按顺序在父样本2中找没有在父样本前半段的基因点，把这些基因点按父样本2的顺序加入到子个体中，直到个体的基因长度等于种群基因长度。在基因突变时，生成两个随机数，代表两个基因位置，然后交换这两个位置的值就行了。

3.程序流程
1、根据输入的城市初始化基因序列；
2、计算每个基因序列的适应性，适应性与路径长度成反比（这里我使用路径长度的倒数表示个体适应性）；
3、根据个体适应性选择生存下来的个体，也就是根据阈值选择留下来的个体；
4、选择后，个体数小于种群初始个体数，使用轮盘选择方式选择父本；
5、若是选中的父本既定概率大于交叉概率，则直接保留下来，否则通过交叉产生后代
6、后代进行基因突变操作，也就是交换两个节点值；
7、判断是否达到迭代次数，是，结束，返回最优解；否，转到第2步。

4.核心伪代码
本文算法使用python实现：

class Life(object):  #一个生命个体
    def __init__(self, gene = None):
        self.gene = gene
        self.score = -1.0
    def setScore(self, v):
        self.score = v

for i in range(0, self.gene_length):  #使用欧式距离表示两个城市距离，也就是个体适应性的倒数
            for j in range(0,self.gene_length):
                self.dist_matrix[i*100+j] = math.sqrt((coordinates[i][0]-coordinates[j][0])*(coordinates[i][0]-coordinates[j][0])+(coordinates[i][1]-coordinates[j][1])*(coordinates[i][1]-coordinates[j][1]))

def make_life(self): #随机产生新个体
    lst = list(range(self.gene_length))
    random.shuffle(lst)
return lst

#演化至下一代
def next(self):
       self.judge()
       newLives = []
       newLives.append(Life(self.best.gene)
       while(len(newLives) < self.life_count):
           newLives.append(self.bear())
       self.lives = newLives
       self.generation += 1

#产生下一代
    def bear(self):
        lf1 = self.get_onelife()
        lf2 = self.get_onelife()
        # 交叉
        r = random.random()  #交叉概率
        if r < self.overlapping_rate:   #交叉概率如果大于既定概率，不然就认为这个样本是强样本，直接留下来
            gene = self.overlapping_func(lf1, lf2)
        else:
            gene = lf1.gene
        r = random.random()
        if r < self.mutation_rate:    #当变异概率小于初定的概率，则突变
            gene = self.mutation_func(gene)
            self.mutation_count += 1  
        return Life(gene)

# 交叉函数
    def overlapping_func(self, lf1, lf2):
        p2 = random.randint(1, self.gene_length – 1)
        g1 = lf2.gene[0:p2] + lf1.gene
        g11 = []
        for i in g1:   
            if i not in g11:
                g11.append(i)
        return g11

#变异函数：交换两个位置基因值
def mutation_func(self, gene):
        p1 = random.randint(0, self.gene_length - 1)
        p2 = random.randint(0, self.gene_length - 1)
        while p2 == p1:
            p2 = random.randint(0, self.gene_length - 1)
        gene[p1], gene[p2] = gene[p2], gene[p1]
        gene.append(gene[p2])
        del gene[p2]
        return gene

5.代码运行及测试
为了了解不同参数设置对最终路径的影响，本文对不同交叉概率、变异概率以及种群个体数做了不同的实验。这里数据我使用了中国34个省以及自治区、特别行政区的经纬度作为TSP中的34个城市坐标。

5.1 交叉概率：当生命个体数为30，变异概率为0.03时，不同交叉概率的结果如下图1所示，可以看到当交叉概率为0.8时，得到的路径最短。

5.2 不同变异概率：交叉概率为0.8，种群数为30，不同变异概率的路径长度结果如图2所示，可以看到，当变异概率为0.03时，得到的路径最短。

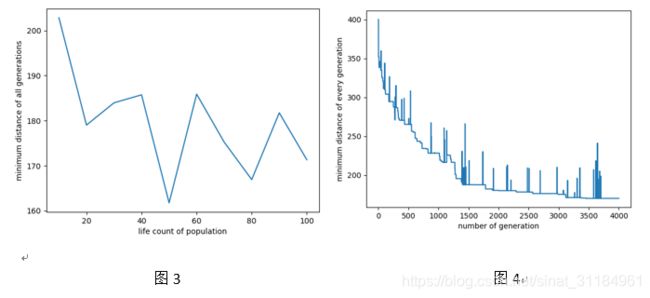
5.3 不同个体数：交叉概率0.8，变异概率为0.03，不同个体数的路径长度如图3所示，可以看到，当种群数目为50 时，得到的路径最短。

5.4 根据迭代次数，路径的收敛图4，这里交叉率为0.8，变异率0.03，个体数50。

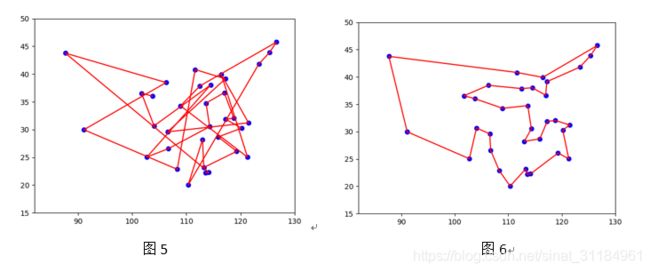
5.5 初始路径图（图5），最终路径图（图6）。此时路径长度为168，可以看到初始的路径中有许多重叠的路径，而最终得到的路径已经没有重叠了，也就是找到了最短的路径，在实验的过程中发现不同的参数对整个路径的影响程度还是蛮大的，不同参数的设置可能会使路径长度在的不同在40左右波动，图8的结果只是我的一次结果，可能还会有更好的结果，毕竟我们只是找近似的全局最优解。