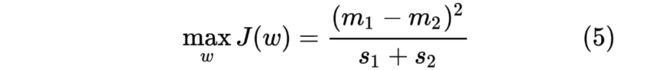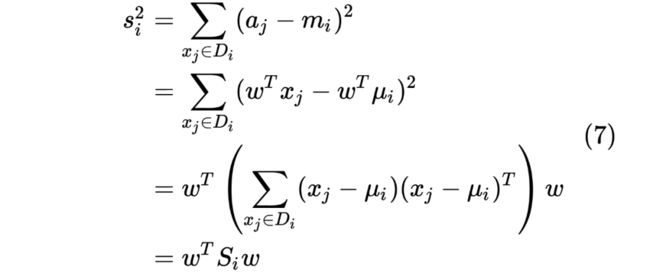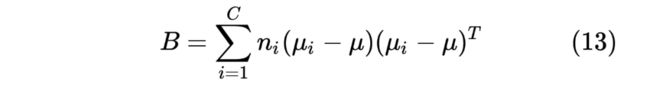深入浅出线性判别分析（LDA），从理论到代码实现

©作者｜善财童子

学校｜西北工业大学

研究方向｜机器学习/射频微波

在知乎看到一篇讲解线性判别分析（LDA，Linear Discriminant Analysis）的文章，感觉数学概念讲得不是很清楚，而且没有代码实现。所以童子在参考相关文章的基础上在这里做一个学习总结，与大家共勉，欢迎各位批评指正~~

注意：在不加说明的情况下，所有公式的向量均是列向量，这个也会反映到代码中。

本文的基本思路来自以下文章：

https://www.adeveloperdiary.com/data-science/machine-learning/linear-discriminant-analysis-from-theory-to-code/

基本概念和目标

线性判别分析是一种很重要的分类算法，同时也是一种降维方法（这个我还没想懂）。和 PCA 一样，LDA 也是通过投影的方式达到去除数据之间冗余的一种算法。

如下图所示的 2 类数据，为了正确的分类，我们希望这 2 类数据投影之后，同类的数据尽可能的集中（距离近，有重叠），不同类的数据尽可能的分开（距离远，无重叠），左图的投影不好，因为 2 类数据投影后有重叠，而右图投影之后可以很好地进行分类，因为投影之后的 2 类数据之间几乎没有重叠，只是类内重叠得很厉害，而这正是我们想要的结果。

正交投影

因为 LDA 用到了投影，所以这里有必要科普一下投影的知识。以二维平面为例，如图所示

我们要计算向量 在 上的投影 ，很显然 与 成比例关系： ，其中 是一个常数。我们使用向量正交的概念来求出这个常数 。在上图中，向量 ， 与 垂直，它们的内积为 0，即 ，即

注意：对于两个向量 x 和 y，  ，所以有 。

假设 w 是一个单位向量，则 ，这样，对于任意向量 x，其在 w 上的投影 可表示为：

其中，  是一个常数。

对于一个数据集 ，其中 ，i=1,2,3,...m 是 d 维列向量。同样假设 w 是一个单位向量，那么每一个 在 w 的投影是：

上述公式的 是叫做 在 w 上的偏移或者坐标。这一系列的值 表示我们做了一个映射 ，即通过投影，我们将 d 维向量降维到了 1 维。

投影数据的均值

为简化起见，我们先假设有 2 类数据，定义样本 ： ，其中 。

我们再定义 ：

其中 是类别， 是所有类别为 的样本的集合。所有数据 投影到 w 后，求其均值：

其中， 是 数据集的均值，同理 的均值是 ，投影后的均值 。为了使投影之后数据可正确地分类，我们希望这 2 类数据的中心离得越远越好，也就是要使 最大，但是单独这个条件并不能保证能够正确地对每一个数据进行分类，我们还需要考虑每一类数据的方差，大的方差表示 2 类数据之间有重叠，小的方差表示 2 类数据之间没有重叠。

LDA 并没有直接使用方差的计算公式，而是采用如下的定义：

这个有个名称叫 scatter matrix，本文暂时将其翻译成散步矩阵吧。

总结一下，LDA 主要就两点：

（1）最大化各类数据中心的距离，也就是各类数据的均值之间的距离要最大；

（2）各类数据的散步矩阵之和要小，也就是每个类别中的数据尽可能地集中。

将上述两点整合在一起，得到一个优化公式：

这个公式也叫做 Fisher LDA，这样，LDA 的问题就是关于  最优化上述的公式。我们重写上述公式如下：

同理有  ：

这样：

这样，LDA 目标优化函数就可以重写为：

对公式（9）关于  求导，并令其导数为 0，可得：

整理得：

公式（11）中 做了替代： ， 是一个常量。如果 S 是非奇异矩阵，那么公式（11）左乘 得到：

最终，LDA 问题其实就是求 对应最大特征值，而我们前面要求的投影方向就是最大特征值对应的特征向量，我们将 LDA 问题化成了矩阵的特征值和特征向量的问题了。

上述推导针对二分类问题进行的，对于多分类问题， 矩阵的计算方式不变，而 矩阵需要采用如下的公式计算：

其中：

C 表示类别的个数； 表示第 i 类中样本的个数； 表示第 i 类样本的均值； 表示整个样本的均值。

关于矩阵微分可参考如下文章：

https://zhuanlan.zhihu.com/p/24709748

https://zhuanlan.zhihu.com/p/24863977

这里提醒一下，对 关于 x 求导的结果是 ，如果 A 是对称矩阵，即 ，则 。公式（10）中因为 B 和 S 都是对称矩阵（由它们的定义可以看出是对称矩阵），所以对 关于 w 求导的结果是  2Bw ，即 ，同理 。

代码实现

import numpy as np
from sklearn import datasets

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

class MyLDA:
    def __init__(self):
        pass


    def fit(self, X, y):
        # 获取所有的类别
        labels = np.unique(y)
        #print(labels)
        means = []
        for label in labels:
            # 计算每一个类别的样本均值
            means.append(np.mean(X[y == label], axis=0))
        # 如果是二分类的话
        if len(labels) == 2:
            mu = (means[0] - means[1])
            mu = mu[:,None] # 转成列向量
            B = mu @ mu.T
        else:
            total_mu = np.mean(X, axis=0)
            B = np.zeros((X.shape[1], X.shape[1]))
            for i, m in enumerate(means):
                n = X[y==i].shape[0]
                mu_i = m - total_mu
                mu_i = mu_i[:,None] # 转成列向量
                B += n * np.dot(mu_i, mu_i.T)

        # 计算S矩阵
        S_t = []
        for label, m in enumerate(means):
            S_i = np.zeros((X.shape[1], X.shape[1]))
            for row in X[y == label]:
                t = (row - m)
                t = t[:,None] # 转成列向量
                S_i += t @ t.T
            S_t.append(S_i)
        S = np.zeros((X.shape[1], X.shape[1]))
        for s in S_t:
            S += s

        # S^-1B进行特征分解
        S_inv = np.linalg.inv(S)
        S_inv_B = S_inv @ B
        eig_vals, eig_vecs = np.linalg.eig(S_inv_B)

        #从大到小排序
        ind = eig_vals.argsort()[::-1]
        eig_vals = eig_vals[ind]
        eig_vecs = eig_vecs[:, ind]
        return eig_vecs


#构造数据集
def make_data(centers=3, cluster_std=[1.0, 3.0, 2.5], n_samples=150, n_features=2):    
    X, y = make_blobs(n_samples, n_features, centers, cluster_std)
    return X, y

if __name__ == "__main__":
    X, y = make_data(2, [1.0, 3.0])
    print(X.shape)

    lda = MyLDA()
    eig_vecs = lda.fit(X, y)
    W = eig_vecs[:, :1]

    colors = ['red', 'green', 'blue']
    fig, ax = plt.subplots(figsize=(10, 8))
    for point, pred in zip(X, y):
        # 画出原始数据的散点图
        ax.scatter(point[0], point[1], color=colors[pred], alpha=0.5)
        # 每个数据点在W上的投影
        proj = (np.dot(point, W) * W) / np.dot(W.T, W)

        #画出所有数据的投影
        ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.5)

    plt.show()

4.1 2类2个特征

if __name__ == "__main__":
    X, y = make_data(2, [1.0, 3.0]) #rint(X.shape)

    lda = MyLDA()
    eig_vecs = lda.fit(X, y)
    W = eig_vecs[:, :1]

    colors = ['red', 'green', 'blue']
    fig, ax = plt.subplots(figsize=(10, 8))
    for point, pred in zip(X, y):
        # 画出原始数据的散点图
        ax.scatter(point[0], point[1], color=colors[pred], alpha=0.5)
        # 每个数据点在W上的投影
        proj = (np.dot(point, W) * W) / np.dot(W.T, W)

        #画出所有数据的投影
        ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.5)

    plt.show()

运行结果是：

可见，数据投影后在 1 维上可以很好的分类。

4.2 3类2个特征

if __name__ == "__main__":
         # 3类
    X, y = make_data([[2.0, 1.0], [15.0, 5.0], [31.0, 12.0]], [1.0, 3.0, 2.5])
    print(X.shape)

    lda = MyLDA()
    eig_vecs = lda.fit(X, y)
    W = eig_vecs[:, :1]

    colors = ['red', 'green', 'blue']
    fig, ax = plt.subplots(figsize=(10, 8))
    for point, pred in zip(X, y):
        # 画出原始数据的散点图
        ax.scatter(point[0], point[1], color=colors[pred], alpha=0.5)
        # 每个数据点在W上的投影
        proj = (np.dot(point, W) * W) / np.dot(W.T, W)

        #画出所有数据的投影
        ax.scatter(proj[0], proj[1], color=colors[pred], alpha=0.5)

    plt.show()

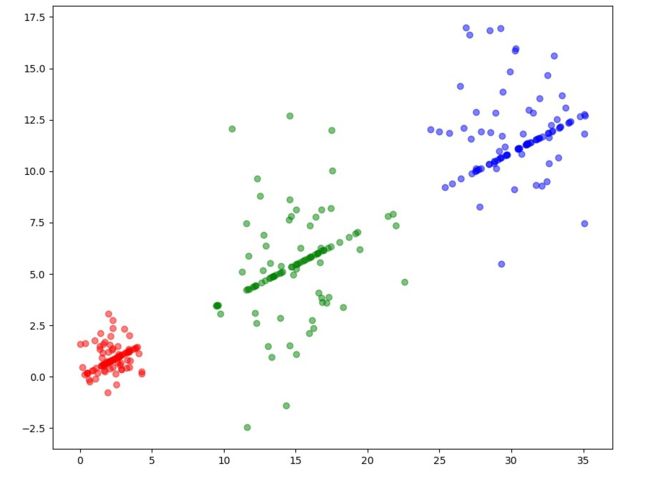
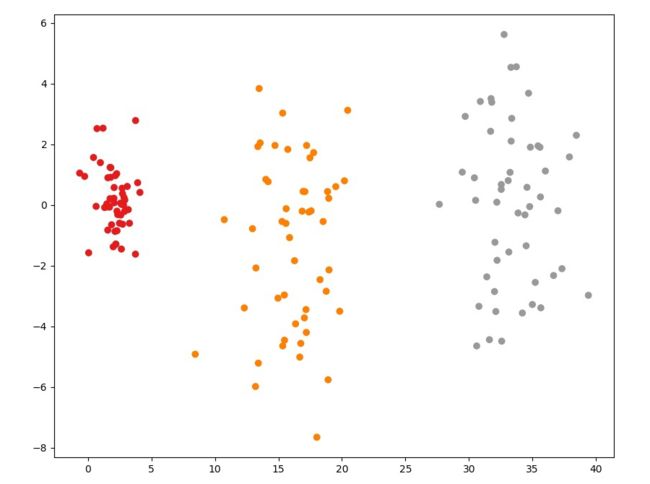
运行结果是：

4.3 3类4个特征

if __name__ == "__main__":
    #X, y = load_data(cols, load_all=True, head=True)
    X, y = make_data([[2.0, 1.0], [15.0, 5.0], [31.0, 12.0]], [1.0, 3.0, 2.5], n_features=4)
    print(X.shape)

    lda = MyLDA()
    eig_vecs = lda.fit(X, y)

    # 取前2个最大特征值对应的特征向量
    W = eig_vecs[:, :2]

    # 将数据投影到这两个特征向量上，从而达到降维的目的
    transformed = X @ W
    plt.subplots(figsize=(10, 8))
    plt.scatter(transformed[:, 0], transformed[:, 1], c=y, cmap=plt.cm.Set1)
    plt.show()

运行结果如下：

对上述结果使用 sklearn 官方实现的 LDA 进行对比验证：

if __name__ == "__main__":
    X, y = make_data([[2.0, 1.0], [15.0, 5.0], [31.0, 12.0]], [1.0, 3.0, 2.5], n_features=4)
    print(X.shape)

    lda = MyLDA()
    eig_vecs = lda.fit(X, y)

    # 取前2个最大特征值对应的特征向量
    W = eig_vecs[:, :2]

    # 将数据投影到这两个特征向量上，从而达到降维的目的
    transformed = X @ W
    plt.subplots(figsize=(10, 8))
    plt.scatter(transformed[:, 0], transformed[:, 1], c=y, cmap=plt.cm.Set1)
    plt.title('self-implementation')

    from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
    sk_lda = LinearDiscriminantAnalysis()
    sk_lda.fit(X, y)
    transformed = sk_lda.transform(X)
    plt.subplots(figsize=(10, 8))
    plt.scatter(transformed[:, 0], transformed[:, 1], c=y, cmap=plt.cm.Set1)
    plt.title("sklearn's offical implementation")
    plt.show()

左图是本文实现的 LDA 分类结果，右图是官方实现的 LDA 分类结果，可见，两者的结果是一致的。

总结

LDA 是一个很强大的工具，但它是一个有监督的分类算法，PCA 是一个无监督的算法，这是和 PCA 的一个很重要的区别。

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

???? 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

???? 投稿邮箱：

• 投稿邮箱：[email protected] 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

????

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。