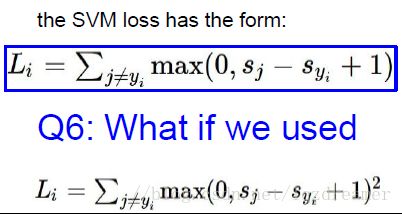斯坦福CS231n深度学习与计算机视觉课程学习笔记(3)——Loss Functions and Optimization
【损失函数】
损失函数是用来告诉我们当前分类器性能好坏的评价函数,是用于指导分类器权重调整的指导性函数,通过该函数可以知道该如何改进权重系数。
而对于多分类SVM(Multiclass SVM)的损失函数,反映了各点间的margin关系,当margin是大于1的,损失函数L是为0,否则是Sj-Syi+1,这就是它的损失,用于指导支撑向量(support vector,SV)的变化,以达到满足所有的SV都能够使各点间的margin大于1.S是通过分类器预测出来的类的分数, Si表示的是第i类分类所得的预测分数,Yi是样本正确分类的标签(即是整数,在讲课中是cifar10,10类标签,即是0-9),i表示是训练集的第i个样本的真实分类的分数。这个式子是在计算真实分类的所得分数与其他分类间的安全距离,也就是margin,如果真实分类的所得分数—其他分类的分数>margin,这就是我们想要的分类效果,安全的分类距离。如果真实分类的所得分数不比其他分类分数高出这么多,就会得到损失,这是不希望看到的。 公式中的“1”,是一个自由参数,即是margin,在SVM的推导中,“1”是可以自由选择的,放大缩小均可以,因为所有的样本的权重会随margin的变化而同等的放大缩小。
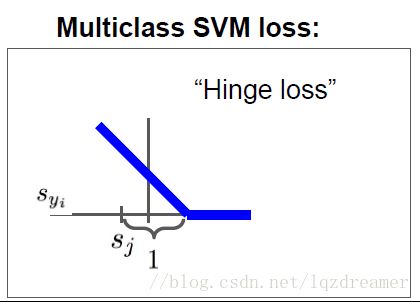
【Hinge Loss】
这是第i类的损失,将所有的损失加起来就是总的损失,是一种Hinge Loss。图像的x轴是Syi,是训练样本真实分类的分数,y轴是Loss,随着真实分类的分数提升是线性下降的,经过一个阈值(margin),损失会变为0,即已成功分类。
Hinge Loss的取值范围为[0,+inf)
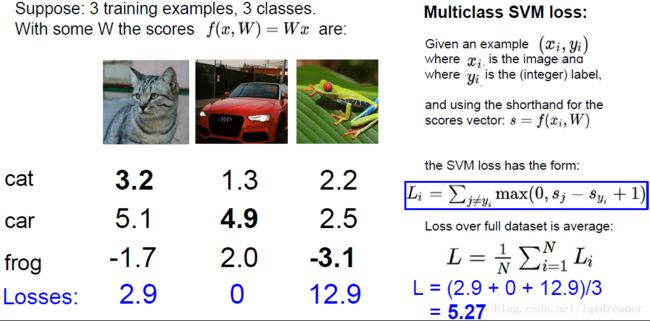
由此,对例子中的进行损失计算为:
第一列分类是cat,分类正确,其他分类的则利用损失函数Li进行计算,car、frog的分类也同样计算。


最后计算数据集的平均损失:
通过以上例子可以看出,Loss反映了真实分类所得分数与其他分类分数的差别,也就是说,如果真是分类所得分数比分类为其他类的分数要低(取分数最高的那一类作为分类输出,那么将分类错误),但是分数低多少,要想真实分类的分数最高,差距在哪,即是通过损失函数Li的值反映出来了。
同时,如果分类正确的分数比其他的分类分数高于1,即使正确分类的分数发生微小变化(相差仍然大于1),那么Hinge Loss仍然有效,损失函数值不会发生变化。
损失函数的也可以进行平方操作,其效果在于对分类错误的刻画程度上,也可以自定义损失函数,用于对实际的分类进行刻画。这是用于权衡各分类之间的效果
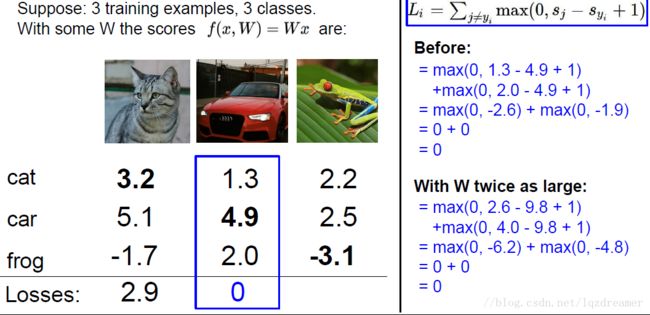
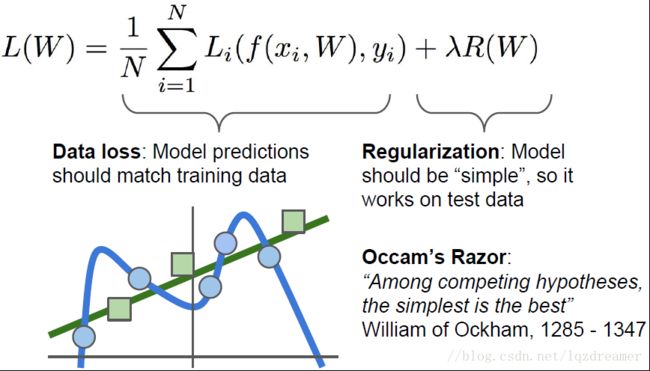
如果损失为0,那么使损失为0的权重矩阵不唯一,例如权重矩阵成倍的变化,只是导致分数的成倍变化,其margin成倍的变化,但是损失仍然为0.损失函数是用来是模型对训练数据进行匹配的,但是匹配有个度,欠拟合导致模型简单,测试效果不好;过拟合,模型较为复杂,泛化性不好。因此在损失函数后加一个正则项,用来鼓励模型以某种方式选择更简单的w。正则项是一个反映模型复杂度的损失项,正则项的系数λ是用来平衡数据损失和正则项损失的超参数,也是交叉验证中需要调整的参数。
【正则项分类】
主要目的是使模型简单化,而不是仅仅拟合数据。

• L2正则化,是一种关于权值向量W的范数,是对权重向量的欧式范数进行惩罚,例如一个权重向量(四维)只有一个元素是1,其他为0,而另一个是全都为0.25,这时第二个范数更小,反映对所有的进行权衡,更具有鲁棒性,而不是仅仅依赖于某个分量
• L1范数具有一些较好的性质,类似于矩阵中的稀疏矩阵,与L2的情况有点相反,更适合使权重稀疏化
• Elastic net(L1+L2),即是L1与L2的组合
• 最大值(max)范数,对最大的权重进行惩罚
• 或者采用dropout,Fancier(批量归一化,随机深度)
因此,需要根据实际情况进行选择合适的范数。
【Softmax Classifier(Multinomial Logistic Regression)】通过上面的计算所得的分数,并没有一个合理的解释,通过利用softmax函数,将所得分数进行归一化,赋予其含义,即得到了相应概率分布(0-1之间,和为1),通过这样所得到的是,当一个样本是猫(比如真实分类),那么概率分布在猫处的概率为1(理想情况下),其他的是0,概率分布即存在一个尖峰。
想要最大化似然函数,即是最小化负对数似然函数那么损失函数为
【Hinge Loss(SVM) vs Softmax】Hinge Loss只是使正确分类的分数比其他分类的分数高出一个margin即可,即是再提高正确分类的分数,也不会对损失函数带来多大的影响,也就是说并没有增加分类正确的有用信息;而Softmax则不同,提高正确分类的分数会增加分类正确的概率,降低其他分类的概率,进一步带来了有用信息,使分类正确的概率越来越高,趋近于0.
但是在实际的运用中,两者使用的差别不是很大。
【小结】
• 策略1:随机搜索 # assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function
bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)
# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)
# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555• Follow the slope(梯度下降):
选取梯度下降最快的方向进行优化。通过是向量中的每一维变化一个步长,导致损失变化,计算该梯度,选取梯度最大的进行权重变化。但是实际计算过程十分缓慢,实际使用的是权重导数dw。
数值梯度:慢,近似,容易实现
分析梯度(Analytic gradient):准确,快速,容易出错
步长是一个超参数,需要进行调试(tips:首先找到合适的学习率和步长)
• 随机梯度下降(SGD):
在每次迭代中,选取一小部分训练样本成为minibatch(小批量) ,大小的选取一般为2的几次幂,like 32,64,128等 ,然后利用这个minibatch来估计误差总和以及实际的梯度。由于是随机,可以将它看成是对真实数值的一种蒙特卡洛估计。这是一种在深度学习神经网络中经常用到的方法。
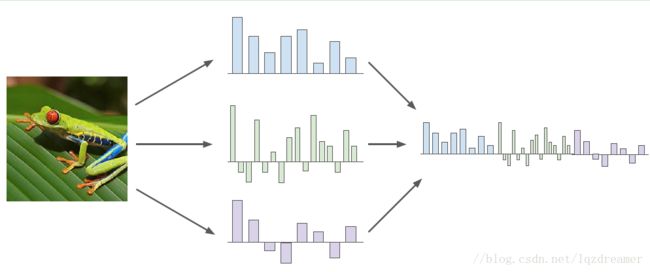
原始图片——>特征提取——>线性分类器

利用特征变换,将非线性的特征分布转换为线性分布。
【方向梯度直方图 Histogram of Oriented Gradients (HoG)】
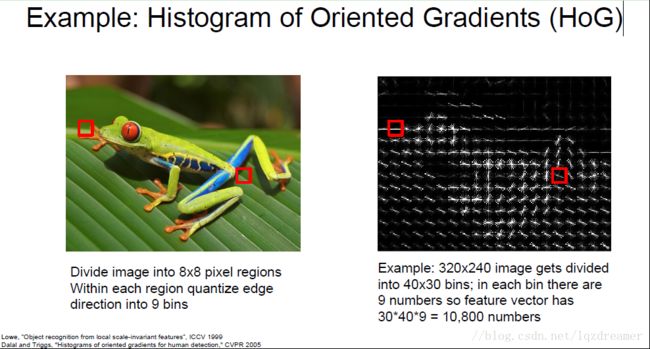
Hubel和Wiesel发现,在人类视觉当中,有向边缘非常重要,特征表示的直方图,尝试提取有向边缘,并测量图像中边缘的局部方向。
方法是,先将图片按八个像素区分为八份,在每个像素区的每一个部分,计算每个像素值的主要边缘方向,将边缘量化到几个组,然后在每一个区域内,计算不同的边缘方向从而得到一个直方图。 这是非常常见的用于目标识别的特征表示
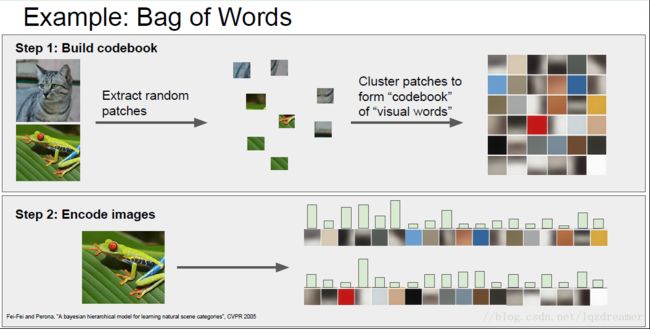
【Bag of Words】
灵感来自于自然语言处理,特征提取是计算一段话中不同词的词频。但是用于图片分类并不简单,分为两阶段:首先是获得一堆图片,从这些图片中进行小的随机块的采样,然后采用K均值等方法将它们聚合成簇,得到不同的簇中心,这些簇中心可能代表了图像中的图片单词的不同类型。