B超从RF信号到B-Mode图像的流程介绍
B
超从
RF
信号到
B-Mode
图像的流程介绍
作者:蒋志强
本人同意他人对我的文章引用,但请在引用时注明出处,谢谢.作者:蒋志强
处理总体流程图
正交解调(Demodulation)
基本流程
正交解调(Demodulation)处理流程最终得到I/Q信号,I/Q信号是我需要用来计算位移估算组织位移进而估算相对杨氏模量的信号。其基本处理流程如下图所示:
Figure 1
正交解调(SINE/COSINE)
我从实验室拿到的原始RF信号数据是一帧的完整RF数据,包含了128条Beamline的RF数据,用文本编辑器查看如下图:
Figure 2
如图所示,RF数据包含128条Beamline数据存储在一个文件中,每条Beamline有4248(4247+1)个点的数据,数据来自于线性探头,探测深度为8厘米。
为了实验算法,我先实验对单条Beamline数据处理的结果,在Matlab中实验无误后,我再在自己的程序中实现整幅一帧的处理。
将一条Beamline的RF提取出来以后,直接显示其波形,如下图的形式:
Figure 3
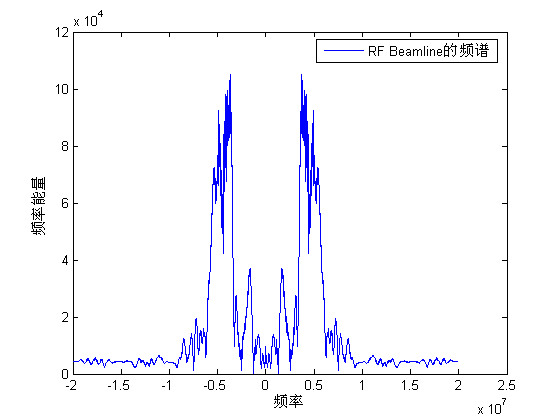
由波形看到,RF Beamline数据在前面很短的地方幅度很大,这是因为探头与身体接触处声阻系数变化比较大,所以超声回声的RF信号幅值很大。将该RF Beamline转化到频率上,并进行中心化处理显示如下:
Figure 4
分析:已知采样频率为40MHz,所以4248点RF信号在时间域上每间隔一个点,对应的时间就是1/40,000,000秒,该段信号采了4248个点的信息,所以信号中包含的各种频率分量中周期最大的是4248/40,000,000秒,做FFT以后频谱的每个单位间隔对应频率应该是:40,000,000/4248 = 9.42K,将频谱的横坐标每个单位换成9.42K显示结果如下:
Figure 5
由上图可以看到信号在+/-5MHz位置附近强度处于峰值,由此可以确定我拿到的RF信号使用的探头的中心频率是5MHz。
对该信号分别乘以cosine和sine得到的in-phase和quadrature信号的频谱显示如下图:
Figure 6
从上图可以看到使用SINE和COSINE处理后,RF信号发生频移,每个原始频率被分解成了两个,每个的幅值为原始的一半,这与书中理论完全相符(《Understanding Digital Signal Processing》《Quadrature Signals Complex, But Not Complicated》,Author:Lyons)。
正交解调(低通滤波处理)
在这一步以后,按照正交解调(Demodulation)的处理流程,需要设计LPF滤波器将大于5MHz的高频信号滤掉,只留下频率在+/-5MHz之间的信号。
5M/20M等于0.25,所以滤波器设计给的截止位置的参数应该取0.25或略微比0.25小一点点(比如0.245),以便于更好的压制5MHz频率以外的信号。我设计的滤波器是使用0.245作为系数,分别得到长度为50,100,200,300,500点的滤波器。其中几个滤波器的频谱响应以及对Q信号滤波后Q信号的频谱如下图(I信号也完全类似):
Figure 7
长度
50
的
LPF
的频谱响应及滤波效果
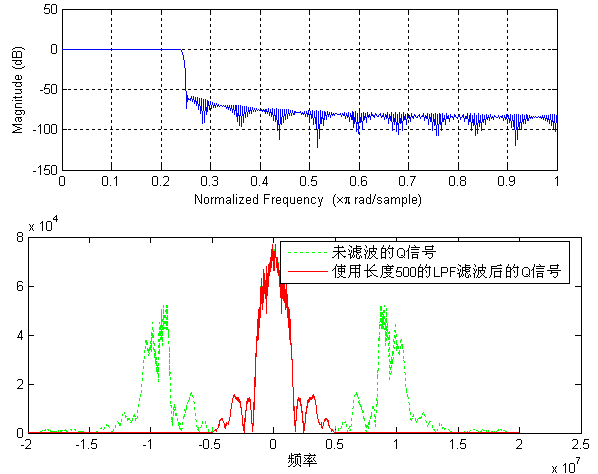
Figure 8
长度
200
的
LPF
的频谱响应及滤波效果
Figure 9
长度
500
的
LPF
的频谱响应及滤波效果
从上面的频谱处理的结果看到,
LPF
长度越长效果越好,在
100
的时候滤波效果已经很不错了,不必为了提高滤波效果将
LPF
设计得过长,不然在做卷积的时候,会增加相当多的乘法运算量而获得的滤波效果改善却微乎其微,实在是很不划算的买卖。
Decimation及Log-Compression
我拿到每条Beamline的点数是4248个,在显示的时候只显示512的长度,所以我需要每隔8.3(4248/512 =8.3)个点取一个点作为最终的显示。为了避免高频谐波的成分的干扰影响,所以还要进行LPF滤波。
Decimation ratio为D = 4248/512 = 8.3,系统采样频率为40MHz,所以Decimation的LPF截止频率应该不大于40M/2D = 2.41MHz;设计滤波器的截止位置给定为1/2D = 0.06。我使用Matlab设计滤波器时给定的截止位置参数就是0.06。
这里对I/Q信号滤波后,每间隔8.3个点取为最后使用的点,将长度缩短为了512个点的I/Q,然后计算Envelop。
下面进行Log-Compression,目的在于将大的灰度范围压缩到PC显示器能够显示的256级灰度范围之内,同时由于Log函数的非线性性质,将对原始数据将暗的区域相对提亮。
我直接代入out = A×Log(1+input) + M;公式进行Log-Compression,input加上1为了避免Log函数的变量小于1导致输出负数,A和M分别决定灰度的动态范围,和整体灰度补偿的程度,用于调整B-Mode图像的视觉效果。出来的图像大小是256*512的矩形,只有128条Beamline,因为是Linear探头,所以进行的扫描转换很简单,每两条Beamline之间做一次线性内插,效果如下图:
A = 55; M = 10; A = 40; M = 0;
A = 35; M = 20; A = 50; M = 15;
上面的图像源自一帧phantom的RF数据,该phantom在中央位置有一个柱状物体。
之前我做过将Decimation处理都是在I/Q计算包络以后再进行,效果和Decimation在I/Q处就进行没有什么视觉上的区别。但Decimation更早的进行,计算包络的时候数据量小很多,将可以节省很多不必要的计算量。
上面叙述的处理流程,是常规的理论上的标准流程,但是在实际的超声系统中,往往不是严格按照这种方式来做,但理解和掌握理论上标准的处理方式也是很重要的。上面虽然介绍了how to do it的具体步骤,但是没有说明why do it in this way。要知道具体的理论原因为什么要这样做,对研究生来说比知道该怎么做更加重要,大家可以参考这些资料真正了解why。《Understanding Digital Signal Processing》第一版,作者是Lyons,该书中解调部分的章节有讲解,特别是该书附录部分对复信号进行了非常好的由浅入深详细讲解,另外Lyons在网上还有一篇更详细讲解的并且可以免费下载的文章《Quadrature Signals Complex, But Not Complicated》对理解这部分的理论部分将会非常有帮助,另外一个叫做Ken Martin老外有一篇名字叫做《Complex Signal Processing is Not-Complex》的文章,只有十几页也可以在网上免费下载,和Lyons的风格类似:把比较复杂的问题简单但透彻地解释得很清楚,而不是故弄玄虚把简单问题故意说复杂。推荐大家用Google scholar去搜索下载这两篇文章,我们会有不少收获的。
这篇说明文章我问过刘老师,刘老师允许放到网上,我再前面加上了个比较详细的流程图,希望可以让大家可以更直观的了解整个流程。唉,总算搞定了。下周又要考6级,回家睡觉了,发篇说明文档也算是攒点人品,大家分点好运给我吧,希望考个对得起咱们川大的分数
: )
The End