Matlab的PCA降维——以Mnist手写数据为例

Matlab的PCA降维——以Mnist手写数据为例

一.参考文章

主成分分析（PCA）原理详解
主成分分析pca（Matlab pca函数参数解释）

二.百度云下载（代码+数据）

PCA sharing
链接：https://pan.baidu.com/s/1Bmfb7rLANU4D1T4q_GEu0A
提取码：4xoh

三.实际操作

1.导入数据

%%
%导入原始数据 放在了E盘
mnist_raw = csvread('E:/by/mnist_train.csv');
%原始数据维度为60000*785，第一列为标签信息 
%譬如第一个为"5"则这个图片是手写的"5"

imgs = mnist_raw(1:1000,2:end);  %选取1000个样本，并去除标签列
imgs = im2double(imgs);

figure(1) %图1显示前50幅图像
for i = 1:50
    subplot(5, 10, i);
    imshow(reshape(imgs(i, :), 28, 28));%28x28=784 共有784列
    %imshow(reshape(imgs(i, :), 40, 40));这样子是错误的
end

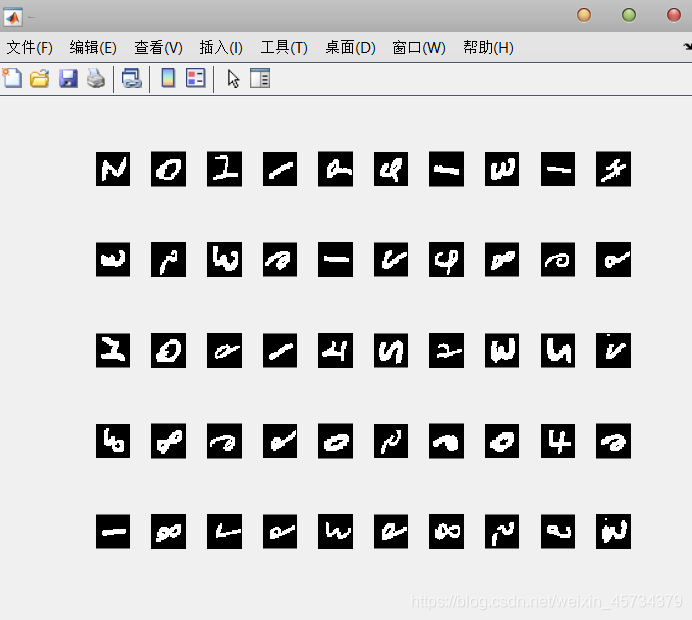
图1如下图所示，每个照片是由28*28的像素构成的，数据中为“0”则是黑色区域，通过数据的第一列的标签值，可以知道图1中第一行的数字分别是5 、0、 4、 1、 9、 2、 1、 3、 1、 4。

2.PCA数据可视化

对于pca()函数的详细解说，请看上面的链接，这部分是最重要也是最难理解的，需要对pca原理有一定的了解

%%
%对数据imgs进行PCA降维
[coeff,score,latent] = pca(double(imgs));
% coeff的每一列是样本协方差矩阵的特征向量（主成分分量）；
%score第i行前n个数值代表着样本i降到n维的结果；
% latent从大到小保存了样本协方差矩阵所有的特征值

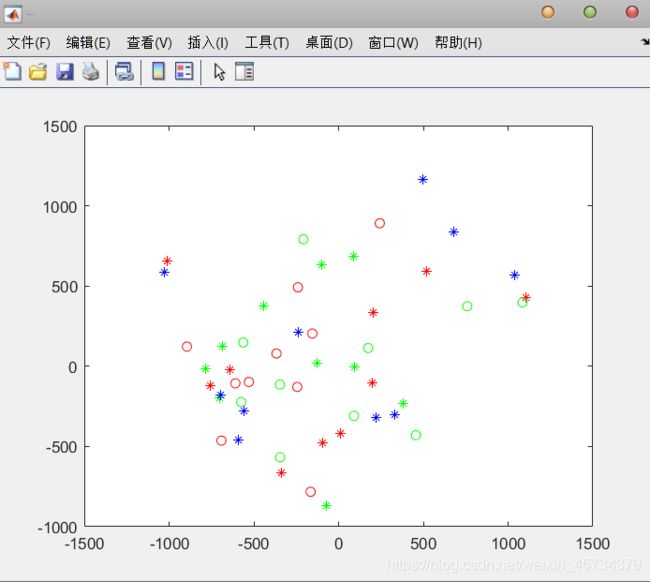
% 取前两维，并可视化如下：
figure(2)
plot(score(1:10, 1), score(1:10, 2), 'r*');
hold on;
plot(score(11:20, 1), score(11:20, 2), 'g*');
hold on;
plot(score(21:30, 1), score(21:30, 2), 'b*');
hold on;
plot(score(31:40, 1), score(31:40, 2), 'go');
hold on;
plot(score(41:50, 1), score(41:50, 2), 'ro');
hold on;

这里我一直不明白为什么要这样画图——每十个样本数据降到2维（降到二维就可以画图了），然后抹上不同的颜色，搞得同一个颜色就是一个类别了。

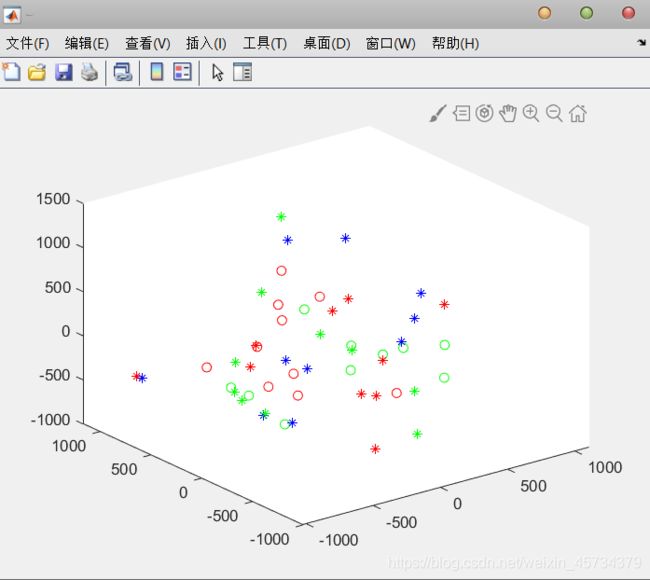
然后我取了前三维，用plot3()函数制作了三维图像，颜色一样的不代表同一个“类别”的（这个下次问问我亲爱的老师），红色圈的仅代表前10个的样本。

3.可视化“特征”

coeff是一个784*784的double

% 可视化“特征”，主成分分量coeff的每一列可以构造一个“特征”，对这些特征可视化如下：
figure(3)
for i=1:25
    subplot(5, 5, i);
    imshow(1.0 - reshape(coeff(:, i), 28, 28));
end

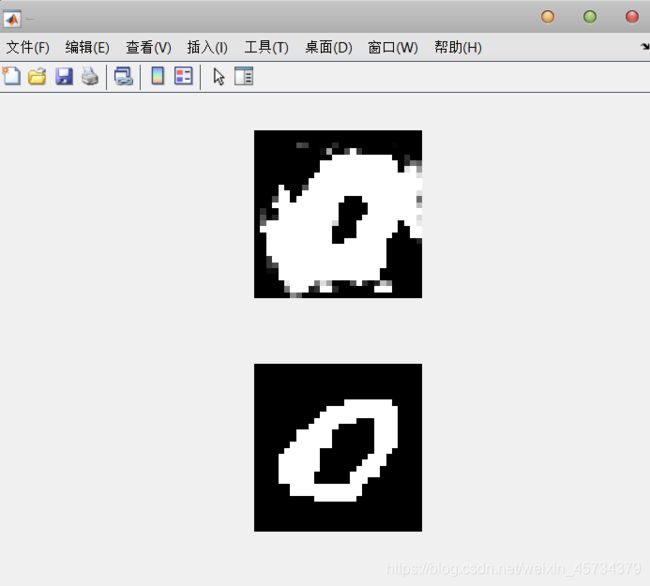
4.重建图像

% score第i行前n个数值代表着样本i降到n维的结果。
%score第i行的第j个数值代表着第j个“特征”在原图像i中的权重。这些权值有正有负。
% 据此，可以重构图像。下面以第二张图像为例。
% 计算样本均值
base_img =  mean(imgs);
img = base_img';
%使用前10个特征重建第二幅图像
for i = 1:10
    img = img + coeff(:, i).*score(2, i);
end
% 显示重建的图像和原始图像，进行比较
figure(4)
subplot(2,1,1);
imshow(reshape(img, 28, 28));
subplot(2,1,2);
imshow(reshape(imgs(2,:), 28, 28));

四.心得

算法原理还是最核心的，这个代码数据啥的只是让大家好好消化比较抽象的PCA原理，写的不够好，希望大家多多交流（大大的微笑）