Continuous control with deep reinforcement learning_ICLR2016

Continuous control with deep reinforcement learning(ICLR2016)
https://arxiv.org/abs/1509.02971v2

Abstract

   作者将Deep-Learning成功的应用于连续动作领域。作者提出了一个基于确定性策略梯度(deterministic policy gradient)的无模型(model-free)的角色批判(actor-critic)算法，它可以在连续的动作空间上运行。使用相同的学习算法、网络架构和超参数，提出的算法解决了20多个模拟物理任务，包括经典问题，如推车摆动、灵巧操作、腿部移动和汽车驾驶。作者的算法能够找到性能与计划算法相媲美的策略，并且可以完全动态的访问域及其导数的变化(dynamics
of the domain and its derivatives)。作者进一步证明，对于多任务，算法可以直接从原始像素输入"端到端"地学习策略。

1.Introduction

   然而，DQN主要地是为了解决高维观测空间问题，但是它只能处理离散和低维作用空间问题。许多有趣的任务，尤其物理控制任务，具有连续(real valued)和高维的动作空间。DQN不能直接应用于连续域，它依赖于寻找使动作值函数最大化的动作，而在连续值的情况下，每一步都需要迭代优化过程。
   将DQN等深度强化学习方法应用于连续域的一个明显方法是将动作空间离散化。然而，有许多限制，最明显的是维数的curse(诅咒):动作的数量随着自由度的数量呈指数级增长。例如，一个7自由度的系统(如人的手臂)，对每个关节进行最粗离散化${\alpha }_i\in \{-k,0,k\}$，将得到维数为$3^7=2187$的动作空间。对于需要对动作进行精细控制的任务，情况甚至更糟，因为它们需要相应的更细粒度的离散化，从而导致离散动作数量的激增。这样大的动作空间很难有效地探索，因此在这种环境下成功地训练类似dqn的网络很可能是棘手的。此外，动作空间的未知离散化(naive discretization)不必要地丢弃关于动作域结构的信息，而这些信息对于解决许多问题可能是至关重要的。
   文章中，作者提出了一个使用深度函数逼近器的model-free、off-policy actor-critic，它可以学习高维连续动作空间中的策略。作者的工作基于确定性策略梯度(DPG)算法，它本身近似于NFQCA,类似的观点可以在(Prokhorov et al., 1997))中找到。然而，正如我们下面所展示的，这种带有神经函数逼近器的 actor-critic方法的 naive application(原生应用) 对于具有挑战性的问题是不稳定的。
   在这里，我们结合了 actor-critic的方法和最近的成功的Deep-Q Network(DQN)。在DQN出现之前，一般认为使用大型非线性函数逼近器学习值函数是困难且不稳定的。DQN之所以能够使用这种函数逼近器来稳定、鲁棒地学习值函数，主要有两点创新:

1. 利用重播缓冲区中的样本对网络进行非策略训练，以最小化样本之间的相关性;
2. 该网络使用target Q-network进行训练，以在时间差异备份时给出一致的目标。在这项工作中，我们利用了相同的思想，以及批处理标准化，这是深度学习的最新进展。

   作者为了评估方法，构造了各种具有挑战性的物理控制问题，包括复杂的多关节运动，不稳定和丰富的接触力学，以及步态行为。其中有典型的问题，如推车问题，以及许多新领域。机器人控制长期以来面临的一个挑战是，如何直接从视频等原始感官输入中学习动作策略。因此，我们在模拟器中放置了一个固定的视点摄像机，并尝试使用低维观测(例如关节角度)和直接从像素点进行所有任务。
   作者提出的的无模型方法，称为Deep DPG(DDPG),可以通过使用相同的超参数和网络结构，使用低维观察(例如笛卡尔坐标或关节角)来学习所有任务的竞争策略。在许多情况下我们也能够直接从像素学习到好的策略，同样保持超参数和网络结构不变。
   该方法的一个关键特征是它的简单性:它只需要一个简单的actor-critic架构和只有很少“moving parts”的学习算法，这使得它易于实现和扩展到更困难的问题和更大的网络。对于物理控制问题，我们将我们的结果与规划师(Tassa等人，2012年)计算的基线进行比较，基线可以完全访问底层模拟动力学及其衍生物(参见补充信息)。有趣的是，DDPG有时会发现策略的性能超过规划者的表现，在某些情况下，甚至在从像素学习时也是如此(规划者总是在底层的低维状态空间上进行规划)。

2.Background

   我们考虑一种标准的强化学习设置，包括与离散时间步长中的环境$E$交互的agent。在每一个时间步$t$，agent接收到一个观察值$x_t$, 采取一个动作，并接收一个标量reward $r_t$。在这里考虑所有环境中，动作都是实值(real-valued)$a_t\in {\mathbb{R}}^N$. 一般情况下，可以对环境局部观察，这样就可能需要观测整个历史，动作对(action pairs) $可以表示的状态为 $s_t=(x_1,a_1,...,a_{t-1},x_t)$。这里，我们假设环境是完全可被观察的，所以$s_t=x_t$.
   agent 的行为是由一个策略$\pi$定义的，该策略将状态映射到动作的概率分布上，即$\pi :\mathcal{S}\to \mathcal{P}(\mathcal{A})$.环境$E$也可能是随机的。我们将其建模为一个具有状态空间$\mathcal{S}$、行动空间$\mathcal{A}={\mathcal{R}}^N$、初始状态分布$p(s_1)$,过渡动态$p(s_{t+1}|s_t,a_t)$、以及reward函数$r(s_t,a_t)$的马尔可夫决策过程。
   状态的回报被定义为未来reward的衰减奖励的综合$R_t={\sum }_{i=t}^T{\gamma }^{(i-t)}r(s_i,a_i)$,其中衰减因子$\gamma \in [0,1]$.注意到回报(reward)依赖于所选择的action，因此依赖于策略$\pi$，并且可能是随机的。强化学习的目标是学习一种策略，是初始分布$J={\mathbb{E}}_{r_i,s_i\sim E,a_i\sim \pi }[R_1]$。我们将策略$\pi$的衰减状态分布表示为${\rho }^{\pi }$.
   动作-价值函数被广泛应用于强化学习算法中。它描述了在state$(s_t)$下采取action $(a_t)$采取行动后的预期reward:$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{r_i\ge t,s_i>t\sim E,a_i>t\sim \pi }[R_t|s_t,a_t]\text{\hspace{1em}(1)}$$
许多强化学习的方法都利用了被称为Bellman方程的递归关系:$$Q^{\pi }(s_t,a_t)={\mathbb{E}}_{r_i,s_{t+1}\sim E}[r(s_t,a_t)+\gamma {\mathbb{E}}_{a_{t+1}\sim \pi }[Q^{\pi }(s_{t+1},a_{t+1})]\text{\hspace{1em}(2)}$$如果目标策略是确定性的，我们可以将其描述为一个函数可记为 $\mu :\mathcal{S}\leftarrow \mathcal{A}$，并避免内部期望:$$Q^{\mu }(s_t,a_t)={\mathbb{E}}_{r_i,s_{t+1}\sim E}[r(s_t,a_t)+\gamma Q^{\mu }(s_{t+1},\mu (s_{t+1}))]\text{\hspace{1em}(3)}$$期望只取决于环境。这意味着我们有可能学习$Q^{\mu }$ off-policy, 通过使用由不同的随机行为策略$\beta$产生的过渡。
Q-Learning ,一种常用的off-policy算法，使用了贪婪策略$\mu (s)=\underset{a}{\mathrm{argmax}}Q(s,a)$. 我们考虑以${\theta }^Q$为参数的函数逼近器，我们通过最小化损失来优化它：$$L({\theta }^Q)={\mathbb{E}}_{s_t\sim {\rho }^{\beta },a_t\sim \beta ,r_t\sim E}[(Q(s_t,a_t|{\theta }^Q)-y_t{)}^2]\text{\hspace{1em}(4)}$$
其中$$y_t=r(s_t,a_t)+\gamma Q(s_{t+1},\mu (s_{t+1})|{\theta }^Q)\text{\hspace{1em}(5)}$$虽然$y_t$也依赖于${\theta }^Q$，但这通常被忽略。
   在过去，常常避免用大的非线性函数逼近器来逼近learning value或action-value，因为理论上不能保证性能，而且实际学习通常不稳定。最近，有人采用Q-learning算法，有效利用大型神经网络作为函数逼近器。他们的算法能够通过像素学习Atari游戏。为了扩大Q-learning的规模，他们引入了两个主要的变化:使用一个回放缓冲区，和一个单独的目标网络来计算$y_t$。我们将在DDPG框架中使用上述方法，并且在下一节中解释它们的实现。

3 Algorithm

   直接将Q-learning应用于连续动作空间是不可能的，因为在连续空间中寻找贪婪策略需要在每一个时间步对$a_t$进行优化; 这种优化对于大型、无约束函数逼近和nontrivial动作空间来说太慢了。在这里，我们使用一种基于DPG算法的actor-critic方法。DPG算法主张了一个参数化的actor函数$\mu (s|{\theta }^{\mu })$,它指定了当前的通过确定地将状态映射到特定的action来制定策略。批评家(critic)$Q(s,a)$是使用Bellman方程来学习的，就像Q-learning一样。通过对actor参数从开始分布$J$的期望收益应用链式法则来更新actor:$$\begin{array}{rl}{\nabla }_{{\theta }^{\mu }}J& \approx {\mathbb{E}}_{s_t\sim {\rho }^{\beta }}[{\nabla }_{{\theta }^{\mu }}Q(s,a|{\theta }^Q){|}_{s=s_t,a=\mu (s_t|{\theta }^{\mu })}]\\ & ={\mathbb{E}}_{s_t\sim {\rho }^{\beta }}[{\nabla }_{a}Q(s,a|{\theta }^Q){|}_{s=s_t,a=\mu (s_t)}{\nabla }_{{\theta }_{\mu }}\mu (s|{\theta }^{\mu }){|}_{s=s_t}]\end{array}\text{\hspace{1em}(6)}$$Silver et al.(2014)证明了这就是策略梯度，即策略执行的梯度。
  与Q learning一样，引入非线性函数逼近意味着收敛性不再有保证。然而，为了在大的状态空间上学习和推广，这些近似器似乎是必不可少的。NFQCA使用与DPG相同的更新规则，但使用神经网络函数逼近，使用批量学习来实现稳定性，这对大型网络来说是难以解决的。NFQCA的一个小批版本在每次更新时不重置策略，这是扩展到大型网络所需要的，相当于我们在这里比较的原始DPG。我们的贡献是在DQN成功的启发下对DPG进行了修改，它允许DQN使用神经网络函数逼近器在线学习大型状态和动作空间。我们将算法称为Deep DPG (DDPG，算法1)。
  当使用神经网络进行强化学习时，一个挑战是大多数优化算法假设样本是独立和同分布的。显然，当在一个环境中顺序探索产生样本时，这个假设就不再成立了。此外，为了有效地利用硬件优化，有必要进行小批量学习，而不是在线学习。
  与DQN一样，作者使用重放缓冲区来解决这些问题。重放缓冲区是有限大小的缓存$\mathcal{R}$.根据探索策略从环境中采样转换(transition),并且元组($s_t,a_t,r_t,s_{t+1}$)存储在重放缓冲区中。当重放缓冲区已满时，丢弃最旧的版本。在每个时间步中，通过从缓冲区中均匀地取样一个小批来更新actor 和 critic。因为DDPG时一种off-policy(离线策略)算法，所以重放缓冲区可能很大，从而允许算法通过一组不相关地transition转换进行学习从而收益。
  用神经网络直接实现Q learning(公式4)在许多环境中被证明是不稳定的。由于更新的网络$Q(s,a|{\theta }^Q)$也用于计算目标值(公式5)，所以Q的更新容易发散。我们的解决方案类似于Mnih et al，2013中使用的目标网络，但对actor-critic进行了修改，并使用"soft"目标更新，而不是直接复制权重。我们创建了一个actor和critic网络的副本，分别时$Q^{\prime }(s,a|{\theta }^{Q^{\prime }})$和${\mu }^{\prime }(s|{\theta }^{{\mu }^{\prime }})$,这个副本用于计算目标值。然后通过让他们慢慢跟踪学习网络来更新这些目标网络的权重：${\theta }^{\prime }\leftarrow \tau \theta +(1-\tau ){\theta }^{\prime }$,其中$\tau \ll 1$. 这就限制了目标值的缓慢变化，极大地提高了学习地稳定性。这个简单的改变使相对不稳定的动作-价值函数学习问题更接近于监督学习的情况，这是一个存在鲁棒性解决方案的问题。我们发现，同时拥有一个target${\mu }^{\prime }$和$Q^{\prime }$需要有稳定的目标$y_i$才能持续训练critic而不产生分歧。这可能会减慢学习速度，因为目标网络会延迟值估计的传播。然而，在实践中，我们发现学习稳定性远远超过了这点。
  当从低维特征向量观察中学习时，观察的不同组成部分可能有不同的物理单位(例如，位置与速度)，并且范围可能因环境而异。这可能使网络难以有效地学习，并可能使它难以找到(在具有不同规模状态值的交叉环境中泛化的)超参数。
  解决这个问题的一种方法是手动缩放功能，使它们在不同的环境和单元中处于相似的范围。为了解决这个问题，我们采用了深度学习最近的一项技术，称为批处理归一化。这项技术对小批量样本中的每个维度进行归一化，以获得单位的均值和方差。此外，它维持(maintains)平均值和方差的运行平均值，用于测试期间的标准化(in our case,在探索或者评估期间)。在深度网络中，它被用来训练过程中最小化协方差偏移(shift)，确保每一层都接收到whitened input(mean 0, unit variance帮助提升训练速度，更快converge).在低维空间下，我们在动作输入之前对状态输入和所有的layers的$\mu$网络和所有$Q$网络的所有层使用batch normalization(网络细节再补充材料中给出)。通过批量标准化，我们能够有效地学习具有不同类型单元的许多不同的任务，而无需手动确保单元在设定范围内。
  在持续行动空间中学习的一个主要挑战是探索。off-policies算法(如DDPG)的一个优点是，我们可以独立于学习算法来处理探索问题。通过将从噪声过程N中采样的噪声添加到actor策略中，我们构建了一个探测策略${\mu }^{\prime }$$${\mu }^{\prime }(s_t)=\mu (s_t|{\theta }_t^{\mu })+\mathcal{N}\text{\hspace{1em}(7)}$$$\mathcal{N}$可以选择适合的环境。
  如补充材料中所详述的，我们使用了Ornstein-Uhlenbeck过程(Uhlenbeck & Ornstein, 1930)来生成时间相关探索(exploration)，以提高物理控制惯性问题的勘探效率(Wawrzy’nski, 2015)。

4 Results

  我们构建了不同难度级别的模拟物理环境来测试我们的算法。这包括了经典的强化学习环境，如cartpole,以及困难的高维任务，比如gripper.任务包括接触，如冰球攻击(canada)和移动任务，如cheetah。在除cheetah外的所有领域中，所有区域的动作都是施加到被驱动关节上的力矩。这些环境使用MuJoCo进行模拟(Todorov et al.， 2012)。图1显示了任务中使用的一些环境的渲染(补充部分包含环境的详细信息，您可以通过https://goo.gl/J4PIAz查看一些了解的策略)。

  在所有的任务中，我们都使用低维状态描述(比如关节角度和位置)和高维环境渲染来进行实验。如DQN (Mnih等，2013年;为了使问题在高维环境中几乎可以完全观察，我们使用了动作重复。对于agent的每个时间步长，我们将模拟分为3个时间步长，每次都重复agent的动作并进行渲染。因此，观察者报告给agent的观察结果包含9个feature map(3个渲染中每个的RGB)，这允许agent使用帧之间的差异来推断速度。帧被下采样为64x64像素，8位RGB值被转换为浮点，缩放为[0,1]。有关我们的网络结构和超参数的详细信息，请参阅补充信息。
  我们通过在没有探索噪声的情况下进行测试来定期评估策略。 图2显示了一系列环境的性能曲线。 我们还报告了删除了算法组件（即目标网络或批量标准化）的结果。 为了在所有任务中表现良好，这两项添加都是必要的。 特别是，在没有目标网络的情况下学习，就像在使用DPG的原始工作中一样，在许多环境中非常糟糕。

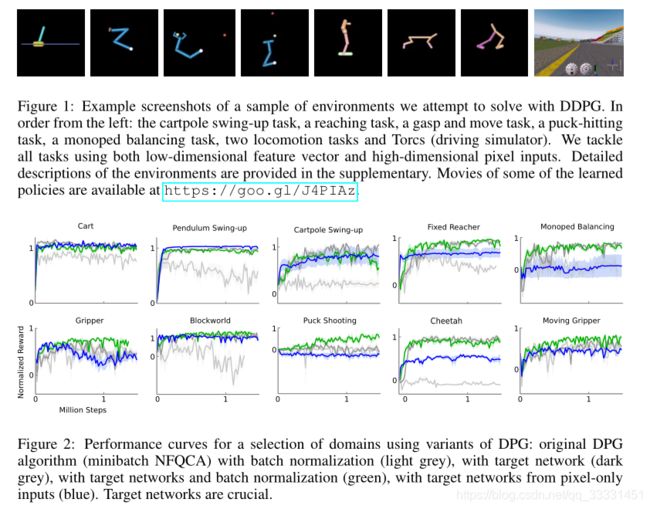
  Surprisingly, 在一些更简单的任务中，从像素学习策略和使用低维状态描述学习一样快。这可能时由于重复操作使问题更加简单。还有一种可能是，卷积层提供一种很容易分离的状态空间表示，这对于较高层的快速学习很简单。
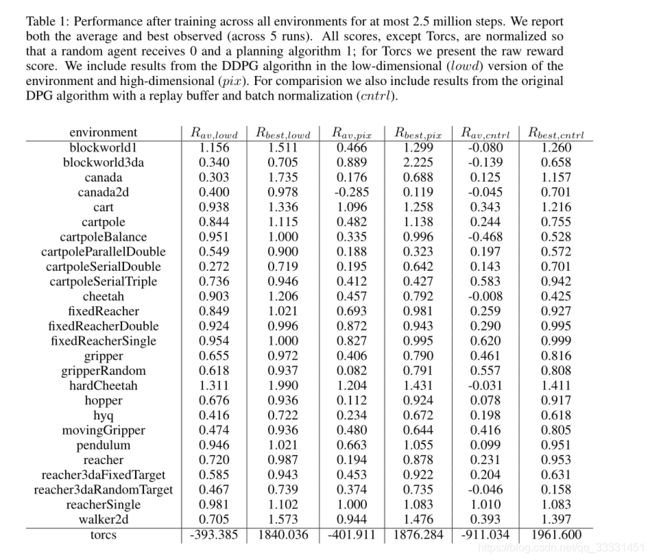
  表1总结了DDPG在所有环境中的性能(结果是5个副本的平均值)。我们使用两个基线标准化分数。第一个基线是一个naive策略的平均回报，该策略在有效的动作空间上对均匀分布的动作进行采样。第二个基线是iLQG(Todorov & Li, 2005)，这是一个基于规划的求解器，可以完全访问底层物理模型及其导数。我们对分数进行标准化，使得naive policy的平均得分为0,iLQG的平均得分为1。DDPG能够在许多任务上学习好的策略，而且在许多情况下，一些副本学习的策略优于iLQG找到的策略，即使直接从像素学习也是如此。
  学习准确的价值评估是很有挑战性的。例如，Q-learning容易高估价值(Hasselt, 2010)。我们通过比较训练后Q估计的值与测试片段中看到的真实回报，以经验的方式检验了DDPG的估计。图3显示，在简单任务中，DDPG没有系统偏差，可以准确地估计收益。对于难度较大的任务，Q值估计更差，但DDPG仍然能够学习好的策略。
  为了演示我们的方法的普遍性，我们还包括了Torcs，一款赛车游戏，其中的动作包括加速、刹车和转向。Torcs曾被用作实验在其他策略学习方法。我们对物理任务使用了相同的网络架构和学习算法超参数，但是由于所涉及的时间尺度非常不同，我们在探索中改变了噪声过程。在低维度和像素上，一些副本能够学习到合理的策略，这些策略能够绕轨道完成一个回路，而其他副本无法学习到合理的策略。

5. Related work

   原始的DPG论文用玩具问题评估算法使用瓷砖编码和线性函数逼近。它证明了off-policy DPG在数据效率方面优于off-policy 随机actor critic。它还解决了一个更具挑战性的任务，即多关节章鱼的手臂必须用手臂的任何部分击中目标。然而，那篇论文并没有像我们在这里展示的那样，将这种方法扩展到大的、高维的观察空间。
   人们常常认为，标准的策略检索方法，例如目前工作中探索的方法，实在太脆弱，无法扩展到难以解决的问题(Levine et al., 2015). 标准策略检索被认为是困难的，因为它同时处理复杂的环境动态和复杂的策略。事实上(Indeed)，过去大多数关于actor-critic和策略优化方法的工作都很难扩大到更具有挑战性的问题(Deisenroth等人，2013年)。通常(typically)，这是由于学习的不稳定性造成的，问题的进展要么被后续的学习更新破坏，要么学习速度太慢而不实用。
   最近对无模型策略搜索的研究表明，它可能不像以前想象的那样脆弱。Wawrzynski (2009); Wawrzynski＆Tanwani（2013）使用重放缓冲器在actor-critic框架中训练随机策略。 在我们的工作的同时，Balduzzi & Ghifary（2015）将DPG算法扩展为“偏离器”网络，该网络明确地学习$\delta Q/\delta a$。 但是，他们只在两个低维域上训练。Heess等人引入SVG(0)，它使用Q-critic，但学习了随机策略。DPG可以看作SVG(0)的确定极限。我们在这里描述用于缩放DPG的技术也可以通过使用重参数化技巧来应对随机策略。
   另一个方法，信任域策略优化(TRPO)直接构造随机神经网络策略，而不需要将问题分解为最优控制和监督阶段。该方法通过对策略参数进行精心选择的更新，约束更新以防止新策略偏离现有策略，从而产生近乎单调的改进，这种方法不需要学习动作值函数，而且(可能因此)数据效率明显降低。
   为了应对actor-critic方法的挑战，最近使用引导策略搜索(GPS)算法的工作（例如，（Levine等人，2015））将问题分解为三个相对容易解决的阶段：首先，它利用全状态观测来建立一个或多个标称轨迹周围动力学的局部线性近似，然后使用最优控制来寻找沿着这些轨迹的局部线性最优策略；最后，它使用监督学习来训练一个复杂系统，非线性策略（如深层神经网络），以再现优化轨迹的状态到动作映射。
   这一方法已经成功地应用于多种实际操作中，其中包括各种各样的操作效率。在这些任务中，GPS使用与我们类似的卷积策略网络，但有两个明显的例外：1。它使用一个空间softmax将视觉特征的维数降到每个特征mapping的一个(x,y)坐标系中。该策略还接收有关机器人在网络中第一个完全连接层的配置的直接低维状态信息。这两种方法都可能提高算法的功耗和数据效率，并且可以很容易地在DDPG框架中利用。
   PILCO（Deisenroth&Rasmussen，2011）使用高斯过程来学习非参数的、概率的动力学模型。使用这个学习的模型，PILCO计算分析策略梯度，并在许多控制问题中获得令人印象深刻的数据效率。然而由于高计算需求，PILCO对于高维问题“不切实际”，深度函数逼近器似乎是最有前途的方法，以缩放强化学习到大，高维领域。Wahlström等人(2015）使用深度动态模型网络和模型预测控制，从像素输入解决摆锤摆起任务。他们训练了一个可微的前向模型，并将目标状态编码到学习的潜在空间中。
   Wahlström等人.(2015)使用深度动态模型网络和模型预测控制，从像素输入解决摆锤摆起任务。他们训练了一个可微的前向模型，并将目标状态编码到学习的潜在空间中。他们使用模型预测控制学习的模型来寻找达到目标的策略。然而，这种方法只适用于具有目标状态且能被算法证明的域。
   最近，进化方法已被用于使用压缩权重参数化或无监督学习（Koutnık等人，2014b）从像素学习Torcs的竞争策略，以降低进化权重的维数。目前尚不清楚这些方法对其他问题的推广程度。

6. Conclusion

   这项工作结合了深度学习和强化学习的最新进展，产生了一种算法，该算法能够在连续的动作空间中稳健地解决各种领域中的挑战性问题，即使在使用原始像素进行观察时也是如此。与大多数强化学习算法一样，非线性函数逼近器的使用使任何收敛保证失效；然而，我们的实验结果表明，稳定的学习不需要环境之间的任何修改。
   有趣的是，我们所有的实验使用的经验步骤比DQN学习在Atari领域找到解决方案的步骤要少。我们所研究的几乎所有问题都是在250万步的经验范围内解决的（通常要少得多），比DQN要求的好的Atari解法少20步。这表明，如果有更多的模拟时间，DDPG可能解决的问题甚至比这里考虑的问题更难。
   我们的方法仍然存在一些限制。最值得注意的是，与大多数model-free强化方法一样，DDPG需要大量的训练情节来寻找解决方案。然而，我们认为一个强大的无模型方法可能是大型系统的重要组成部分，它可能会攻击这些限制(Gläscher等人，2010).

Personal understanding

loading…