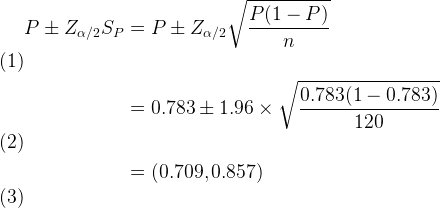统计推断—参数估计—点估计、区间估计、t分布、Z分布
统计推断包括参数估计和假设检验。参数估计就是用样本指标(统计量)来估计总体指标(参数)。
![]()
一、参数估计基础-Z分布
在统计应用中,可以把任何一个均数为![]() ,标准差为
,标准差为![]() 的正态分布
的正态分布![]() 转变为
转变为![]() ,
,![]() 的标准正态分布,即将正态变量值
的标准正态分布,即将正态变量值![]() 用
用![]() 来代替,由于
来代替,由于![]() 服从正态分布,故
服从正态分布,故![]() 服从标准正态分布
服从标准正态分布![]() ,其中
,其中![]() 表示总体的标准差。
表示总体的标准差。
特点:总体的标准差![]() 是一定的。
是一定的。
二、参数估计基础-t分布
实际资料的分析中,由于![]() 往往未知,故标准化转换演变为:
往往未知,故标准化转换演变为:![]() ,服从
,服从![]() 的
的![]() 分布,即:
分布,即:![]() 。其中
。其中![]() 表示样本的标准差,
表示样本的标准差,![]() 表示标准误。
表示标准误。
统计学家发现,t分布的分布性状是与和样本量息息相关的自由度相对应的。![]()
t 分布曲线特点:
-
 分布曲线是单峰分布,它以0为中心,左右对称。
分布曲线是单峰分布,它以0为中心,左右对称。 -
 分布的形状与样本例数
分布的形状与样本例数  (自由度
(自由度 )有关。自由度越小,则
)有关。自由度越小,则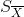 越大,
越大, 值越分散,曲线的峰部越矮,尾部则偏高。
值越分散,曲线的峰部越矮,尾部则偏高。 - 当
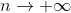 时,则
时,则  逼近
逼近  ,
, 分布逼近标准正态分布。
分布逼近标准正态分布。  分布不是一条曲线,而是一簇曲线。
分布不是一条曲线,而是一簇曲线。
三、参数估计基础-t转换和Z转换的不同
四、参数估计-点估计
用样本统计量直接作为总体参数的估计值。
例 于2000年测得某地27例健康成年男性血红蛋白量的样本均数为125g/L,试估计其总体均数。
![]() ,即认为2000年该地所有健康成年男性血红蛋白量的总体均数为125g/L 。
,即认为2000年该地所有健康成年男性血红蛋白量的总体均数为125g/L 。
缺陷:用样本均值测算总体均值完全相等几乎是不可能的,所以我们用一个范围去估计总体参数所在的位置(区间估计)。
五、参数估计-区间估计
按预先给定的概率![]() 估计总体参数的可能范围,该范围就称为总体参数的
估计总体参数的可能范围,该范围就称为总体参数的![]() 置信区间(confidence interval, CI) 。
置信区间(confidence interval, CI) 。
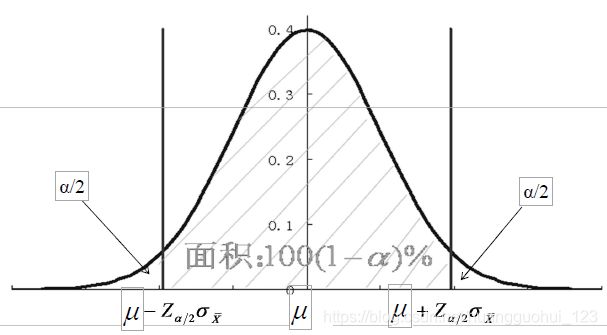
预先给定的概率![]() 称为置信度,常取95%或99%。如无特别说明,一般取双侧95%。
称为置信度,常取95%或99%。如无特别说明,一般取双侧95%。
置信区间由两个数值即置信限(下限和上限)构成。
置信水平是指总体参数值落在样本统计值某一区内的概率(成功率);而置信区间是指在某一置信水平下,样本统计值与总体参数值间误差范围。置信区间越大,置信水平越高。
1、总体均数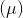 的区间估计
的区间估计
以下是正态总体抽样得到的均数的分布规律,通过抽样得到的样本均数![]() 和
和![]() 并不能原丝合缝的相等。
并不能原丝合缝的相等。
(1)![]() 已知
已知
按标准正态分布原理计算,由![]() 分布,标准正态曲线下有 95%的
分布,标准正态曲线下有 95%的![]() 值在±1.96之间。
值在±1.96之间。
99%的双侧置信区间: ![]() ,99%的双侧置信区间
,99%的双侧置信区间
通式:![]() (双侧)
(双侧)
(2)![]() 未知,样本例数
未知,样本例数![]() 足够大(
足够大(![]() )
)
由![]() 分布可知,自由度越大,
分布可知,自由度越大,![]() 分布越逼近标准正态分布,此时
分布越逼近标准正态分布,此时![]() 曲线下有 95%的
曲线下有 95%的![]() 值在±1.96之间,即:
值在±1.96之间,即:
99%的双侧置信区间: ![]()
通式:![]() (其中
(其中![]() ,
,![]() 表示样本标准差,
表示样本标准差,![]() 表示样本含量,
表示样本含量,![]() 是基于样本标准差
是基于样本标准差![]() 的标准误)(双侧)
的标准误)(双侧)
例 某市2000年随机测量了90名19岁健康男大学生的身高,其均数为172.2cm,标准差为4.5cm,,试估计该地19岁健康男大学生的身高的95%置信区间。
![]() ,
,![]()
该市19岁健康男大学生的身高的95%置信区间(171.3,173.1) cm。
注意:
并不能说该市19岁健康男大学生的平均身高有95%的概率落在区间 (171.3,173.1)里!即不能说这个区间有95%的概率覆盖总体均数。
这是由于平均身高作为总体均值,它是一个常数(客观存在),因此当区间估计完成以后,区间(171.3,173.1)要么覆盖总体均数,要么不覆盖。也就是说,概率为0或1,不会出现其它的概率值。
在一次具体的估计完成之前,一定样本量下的区间估计方法,假如能够重复很多次的话,将有较多的次数,例如95%的次数会成功,有5%的次数会失败,因为在我们完成具体的计算之前,实际上![]() 这个区间估计的上边界和下边界都还是随机变化的。
这个区间估计的上边界和下边界都还是随机变化的。
例 用大量来自同一总体的独立样本对总体均数做估计时,关于95%的置信区间(CI),正确的说法是:A
A.大约有95%的样本的CI覆盖总体均值
B.各个样本估计的CI是相同的
C.对于同一个CI而言,有95%的可能性覆盖总体均数————>>要么覆盖(100%),要么不覆盖(0%)
(3)![]() 未知,且样本例数
未知,且样本例数![]() 较小(
较小(![]() )
)
由![]() 分布可知,此时某自由度的t曲线下约有 95%的
分布可知,此时某自由度的t曲线下约有 95%的![]() 值在
值在![]() 之间,即:
之间,即:
![]()
![]()
![]()
95%的双侧置信区间: ![]()
99%的双侧置信区间: ![]()
通式:![]() (其中
(其中![]() ,
,![]() 表示样本标准差,
表示样本标准差,![]() 表示样本含量,
表示样本含量,![]() 是基于样本标准差
是基于样本标准差![]() 的标准误)(双侧)
的标准误)(双侧)
例 已知某地27例健康成年男性血红蛋白量的均数为 ![]() ,标准差
,标准差![]() ,试问该地健康成年男性血红蛋白量的95%和99%置信区间。
,试问该地健康成年男性血红蛋白量的95%和99%置信区间。
2、总体概率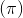
 的区间估计
的区间估计
总体概率的置信区间与样本含量![]() 、阳性频率
、阳性频率![]() (二项分布)的大小有关,可根据
(二项分布)的大小有关,可根据![]() 和
和![]() 的大小选择以下两种方法。
的大小选择以下两种方法。
1、正态近似法
当样本含量足够大,且 ![]() 和
和![]() 不太小(通常
不太小(通常 ![]() 和
和 ![]() 均大于或等于5),则样本率的分布近似正态分布。
均大于或等于5),则样本率的分布近似正态分布。
公式为:![]()
![]() 为样本率,
为样本率, ![]() 为基于样本率的标准误,
为基于样本率的标准误,![]() 。
。
例:用某种仪器检查已确诊的乳腺癌患者94例,检出率为78.3%。估计该仪器乳腺癌总体检出率的95%置信区间。
分析:本例样本例数较大,且样本率![]() 不太小,可用正态近似法:
不太小,可用正态近似法:
2、 查表法
当![]() 较小,如
较小,如![]() ≤50,特别是
≤50,特别是![]() 和
和![]() 接近0或1时,应按照二项分布的原理估计总体率的可信区间。
接近0或1时,应按照二项分布的原理估计总体率的可信区间。
例 某医院对39名前列腺癌患者实施开放手术治疗,术后有合并症者2人,试估计该手术合并症发生概率的95%置信区间。
通过查表,该手术合并症发生概率的95%置信区间为[1%,17%]