Java算法学习——排序算法(简单选择排序,堆排序)
接上一篇文章
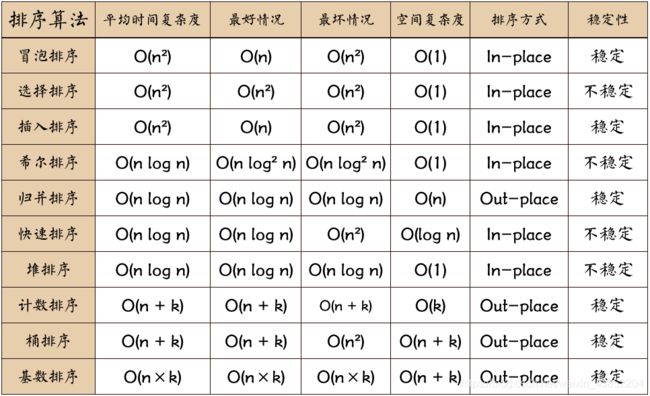
我们依旧把各排序算法的比较图放出来:
1.简单选择排序(Selection Sort):
简单选择排序,最稳定的排序算法之一,无论什么数据进去时间复杂度都是O(n2)。由于时间复杂度较高,所以适用于小规模的数据。它的好处就在于不占用额外的内存空间。
简单选择排序是一种简单直观的排序算法。它的工作原理是:先在未排序的序列中找到最大(小)元素,存放到排序序列的起始位置。然后再从剩余未排序的的序列中,继续寻找最大(小)元素,放到已排序序列的下一个位置,以此类推,直到所有元素均排序完成。
public class SelectionSort {
public static void main(String[] args) {
int[] arr= {
3,2,1,10,9,8,7,5};
for(int i=0;i<arr.length-1;i++) {
for(int j=i+1;j<arr.length;j++) {
if(arr[i]>arr[j]) {
int temp;
temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
}
for(int i=0;i<arr.length;i++) {
System.out.print(arr[i]+"-->");
}
}
}
算法分析:无论什么情况,简单选择排序的时间复杂度均为O(n2)。由于没有占用额外的内存空间,所以时间复杂度为O(1)。但是简单选择排序是不稳定的,两个相等的元素排序后相对位置可能会发生变化。
举个简单的例子,例如:(7) 2 5 9 3 4 [7] 1…当我们利用直接选择排序算法进行排序时候,(7)和1调换,(7)就跑到了[7]的后面了,原来的次序改变了,这样就不稳定了.
2.堆排序(Heap Sort):
堆排序是指利用堆这种数据结构所设计的一种排序算法,也是对简单选择排序的一种改进算法。堆积是一种近似于完全二叉树的结构,并且同时满足堆积的性质,即子节点的键值或索引总是小于(大于)它的父节点。
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
下面我们先来介绍一下堆与数组是如何对应的:
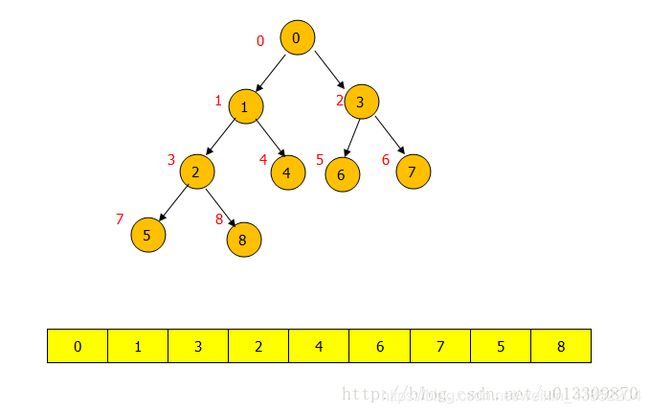
如图所示:表示的是最小堆结构,形式上是一棵完全二叉树,实际存储在内存中的是一个数组,也就是对应下面的数组。树中每一个节点左边红色的值,代表它们在数组中的位置。
父节点与当前节点的下标对应关系为:当前节点下标为 I 则父节点的下标为( I - 1)/2 = Parent , 左孩子节点的下标为:2 * I+1= Lchild ,右节点的下标为:2 * I+2= Rchild 。
堆排序主要有两个过程:
①建堆:对数组建堆可以采用从插入堆的方法,从头结点开始不断的进行插入堆。也可以使用堆化的方法从最后节点的父节点开始进行从下往上进行堆化。
②堆排序:每次选择堆顶元素,并将堆顶元素删除,调整堆后,再重复操作直至堆为空。
堆化(向下调整)、向上调整的前提都是:在二叉树中,只有一个位置不满足堆的性质,其它位置都满足堆的性质。(叶子节点:度为0的节点)
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。而堆就是近似与完全二叉树的结构。
堆化(向上调整)小顶堆:
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] arr= {
14, 10, 9, 7, 12, 2, 1, 4, 3, 11, 5};
System.out.println("arr.length/2="+arr.length/2);
for(int i=arr.length/2-1;i>=0;i--)
{
heapify(arr,i);
//建立堆的过程就是完全二叉树,从下到上调整堆的过程,i=array.length/2-1开始
//依次向上调整,i=array.length/2-1是最后一个节点的父节点i=0是第一个节点
}
System.out.println(Arrays.toString(arr));
}
public class ArraytoHeap {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] arr= {
14, 10, 9, 7, 12, 2, 1, 4, 3, 11, 5};
System.out.println("arr.length/2="+arr.length/2);
for(int i=arr.length/2-1;i>=0;i--)
{
heapify(arr,i);
//建立堆的过程就是完全二叉树,从下到上调整堆的过程,i=array.length/2-1开始
//依次向上调整,i=array.length/2-1是最后一个节点的父节点i=0是第一个节点
}
System.out.println(Arrays.toString(arr));
}
public static void heapify(int[] arr,int i) {
int ld = 2*i+1;
int rd = 2*i+2;
int minpos = i;
if(ld < arr.length && arr[ld] < arr[minpos])
minpos = ld;
if(rd < arr.length && arr[rd] < arr[minpos])
minpos = rd;
if(minpos != i)
{
int temp;
temp=arr[i];
arr[i]=arr[minpos];
arr[minpos]=temp;
heapify(arr,minpos);
}
}
}
插入堆(小顶堆):
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] arr= {
14, 10, 9, 7, 12, 2, 1, 4};
for(int i=0;i<arr.length;i++) {
insertMinHeap(arr,i);
}
System.out.println(Arrays.toString(arr));
}
public class ArraytoHeapFromTop {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] arr= {
14, 10, 9, 7, 12, 2, 1, 4};
for(int i=0;i<arr.length;i++) {
insertMinHeap(arr,i);
}
System.out.println(Arrays.toString(arr));
}
public static void insertMinHeap(int[] arr,int i) {
int parent=(i-1)/2;
while(parent>=0&&arr[i]<arr[parent]) {
// if(i==0) {
// break;
// }
int temp;
temp=arr[i];
arr[i]=arr[parent];
arr[parent]=temp;
i=parent;
parent=(i-1)/2;
}
}
}
堆排序:
public static void main(String[] args) {
int[] arr= {
14, 10, 9, 7, 12, 2, 1, 4};
buildHeap(arr);
//每次选择堆顶元素,并将堆顶元素删除,调整堆后,再重复操作直至堆为空。
for(int i=arr.length-1;i>=0;i--) {
int temp;
temp=arr[i];
arr[i]=arr[0];
arr[0]=temp;
heapify(arr,i,0);
}
System.out.println(Arrays.toString(arr));
}
public static void buildHeap(int[] arr) {
for(int i=arr.length/2-1;i>=0;i--) {
heapify(arr,arr.length,i);
}
}
算法分析:堆排序用分治法把问题规模消减到logn次。建堆的时间为:O(n)。调整堆的时间为:O(logn),所以时间复杂度为:O(nlogn)。也可以这样理解:一共循环n-1次,每次从根节点开始往下循环寻找,每次时间为logn,总时间:(n-1)logn,所以堆排序的时间复杂度为O(nlogn)。
堆排序的表现也十分稳定,最差和最佳的时间复杂度均为:O(nlogn),因此平均的时间复杂度为:O(nlogn)。由于堆排序不需要借助于额外的内存空间,所以它的空间复杂度为:O(1)。
堆排序所排出的序列是不稳定的,两个相等的元素的相对位置可能会发生变化。