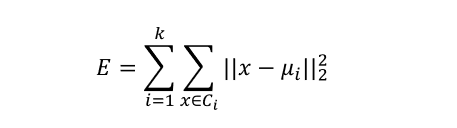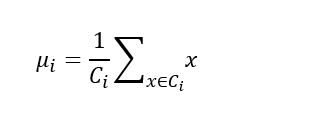基于numpy实现的简单k-means，k-means浅析

基于numpy实现的简单k-means

该文从简单的数据角度讲解基于k-means和基于numpy实现k-means代码。

---

---

前言

k-means是什么，它的做什么的，它与先前所说的聚类有什么关系。

---

一、 k-means

上一篇文章已经详解了聚类，那么基础应该已经没有什么问题了，k-means其实就是用中文来说的话就是k均值聚类，它属于聚类中的"基于原型的聚类"

基于原型的聚类：假设聚类结构能通过一组原型刻画，通常情况下，算法先对原型进行初始化，继而对原型进行不断的更新迭代。而不同的更新方式和不同的求解将产生不同的算法。

k均值算法

官方定义：给定样本集D={x1,x2,…,xn};所谓k均值算法，是求得针对聚类所得簇划分C={C1,C2…,Ck}最小化的平方误差,如下

其中：

那么μi就可以看为是x集合也就是Ci的均值向量。直观的来看，E在一定程度上刻画了簇内的所有样本围绕簇均值向量的紧密程度。E越小则，越紧密，意味着簇内相似度越高。我们只需要求最小E即可。

接下来我们解析官方这些概念和公式：
从概念入手，我们知道最后是要把数据集划分为K个簇，那么"均值"这个俩个字，也很容易理解，从公式入手，所谓的均值其实指的就是均值向量了。那么如果要实现该算法的话，我们只需要几步：

1. 随机选取k个质心，因为要求有k个簇。
2. 接下来求解每个样本到所有质心的距离，并得到最小距离，将该样本归入该质心属于的簇之中
3. 计算簇均值向量
4. 判断簇均值向量是否与上次确定的簇均值向量相等，若相等，则返回簇若不相等，则继续迭代，同时设置迭代上限，防止没有结果的崩溃。

从理论上来说，该方法，适用于所有的数据集，无论是有序属性还是无序属性，需要变更的仅仅是距离的算法问题罢了。

• 显然不难理解，这是k-means的优点之一，同时它还拥有了收敛速度快，聚类效果优，调参简单等优点。

二、代码原理实现

1.引入库

代码如下（示例）：

#基于numpy的K-means
#coding:UTF-8
#倒库
import numpy as np
import random as rd
import matplotlib.pyplot as plt
from math import *

2.面向对象实现

class k_m():
    #计算距离 返回欧氏距离 这里仅仅考虑到了有序属性
    def __init__(self):
        self.color=['.b','.g','.r','.c','.m','.y','.k','.w']
        self.cencolor=['*b','*g','*r','*c','*m','*y','*k','*w']
        #0表示当前颜色的索引
        self.now=0
    def dist(x,y):
        return sqrt(pow(x[0]-y[0],2)+pow(x[1]-y[1],2))
    #crowd_count:簇的个数，也是定义K_means点的个数,传入x坐标和y坐标，
    def k_means(self,x,y,k):
        #获取含有k个随机属性的属性序列 
        k_list=[(x[i],y[i]) for i in rd.sample(range(len(x)),k)] 
        #对属性排序，以便处理
        k_list.sort()
        while 1:
        #crowds为簇列表，每一次遍历都要更新簇列表
            crowds=[[] for i in range(k)]
            for i in range(len(x)):
                t_now=(x[i],y[i]) 
                #计算到所有点的距离 存列表 接下来我们需要该点到所有质心的距离最近并且将其加入簇列表中
                all_dist=[k_m.dist(k_list[j],t_now) for j in range(k)]
                min_dist=all_dist.index(min(all_dist))
                #加入索引之中
                crowds[min_dist].append(i)
            #进入质心的迭代    
            centroid_news_list=[]
            #从之前得到的簇中计算均值，重新确定质心并进行运算
            for i in range(k):
                x_t=sum(x[j] for j in crowds[i])/len(crowds[i])
                y_t=sum(y[j] for j in crowds[i])/len(crowds[i])
                centroid_news_list.append((x_t,y_t))
            centroid_news_list.sort()
            #绘图
            plt.figure()
            plt.title('k={0:d} k-means'.format(k))
            for i in range(k):
                #绘点
                plt.plot([x[j] for j in crowds[i]],[y[j] for j in crowds[i]],self.color[self.now])#
                #绘质心
                plt.plot(k_list[i][0],k_list[i][1],self.cencolor[self.now])#
                self.now+=1
            plt.show()
            plt.close('all')
            if centroid_news_list==k_list:
                return crowds
            else:
                self.now=0
                k_list=centroid_news_list

• 看完代码之后不难发现，该代码非常简单，但同样，其处理能力也有限，因为该代码只是为了从原理角度浅析k-means算法，因此不会用于处理很复杂的数据，但是是其对二元组数据处理仍然十分优秀，这边博主已经用数据集测试过了，代码没有bug可以放心参考。

总结

k-means本身作为原型聚类中最著名的划分聚类算法，以及最为广泛使用的划分聚类算法，其优秀程度自然是不言而喻。有兴趣的小伙伴可以尝试用无序属性的数据集，以及无序距离的计算处理复杂任务，比如物品的分类等等，实现也没有很难，但是十分有用。