【ostep】04 虚拟化 CPU - 进程调度策略

进程调度策略

我们称系统中运行的进程为工作负载（workload），我们对工作负载的假设越具一般性，基于该假设设计的调度策略的表现就越优化。

下面的讨论均假设，工作负载仅占用 CPU，而不发出任何 I/O 操作。

调度指标

调度指标用来衡量不同调度策略的优劣

• 周转时间（turnaround time）

  就是一个任务从交给操作系统到运行结束所用时间。

  工作周转时间 = 工作完成时间 - 工作到达时间

  该指标主要看的是平均周转时间：一段时间内多个任务周转时间的均值。

  平均周转时间 = 周转时间之和 / 工作数量

• 响应时间（response time）

  就是一个任务从交给操作系统到开始运行（操作系统响应了该任务）所用的时间。

  工作响应时间 = 工作首次运行时间 - 工作到达时间

  该指标主要看的是平均响应时间：一段时间内多个任务响应时间的均值。

  平均响应时间 = 响应时间之和 / 工作数量

优化平均周转时间

先进先出（FIFO、FCFS）

先进先出（First In First Out）或称先到先服务（First Come First Served）

思想非常简单，就是哪个工作先到，就先执行谁（直到工作结束）。

在这种策略下，每个任务到达后需要等待前面的任务全部完成后才会得到响应，而其周转时间依赖于先到达工作的执行时间。

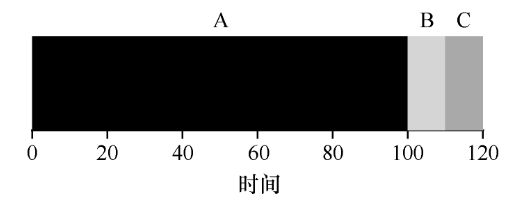
假设 a b c 三个进程陆续同时到达，且运行时间已知，分别为 a b c。

平均周转时间 = [ a + ( a + b ) + ( a + b + c ) ] / 3 = ( 3a + 2b + c ) / 3

平均响应时间 = [ 0 + a + ( a + b ) ] / 3 = ( 2a + b ) / 3

该策略不管是在哪个指标上，都没有很好的针对护航效应（convoy effect）（排队接水问题）进行优化。

最短任务优先（SJF、SPN）

最短任务优先（Shortest Job First）或称最短进程优先（Shortest Process Next）

该策略就是考虑了护航效应的先进先出策略，针对同时到达的多个任务，优先执行耗时最短的任务（贪心）。

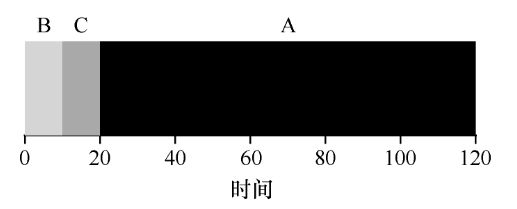
假设 a b c 三个进程陆续同时到达，且运行时间已知，分别为 a b c。

平均周转时间 = [ a + ( a + b ) + ( a + b + c ) ] / 3 = ( 3a + 2b + c ) / 3

平均响应时间 = [ 0 + a + ( a + b ) ] / 3 = ( 2a + b ) / 3

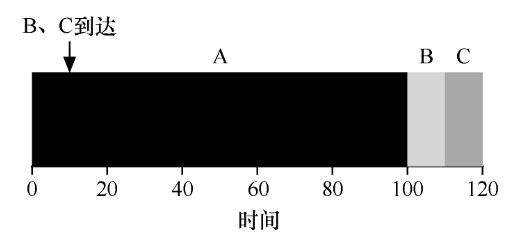
该策略考虑了护航效应，但却仅针对每组同时到达的任务进行了优化。

若 a 任务先到达，策略执行结束后 b c 才到达，此时与先进先出策略没有任何区别：

如果后到达的耗时较短的任务能直接抢占 CPU 就能解决这个问题了。

抢占式最短任务优先（PSJF、STCF）

抢占式最短任务优先（Preemptive Shortest Job First）或称最短完成时间优先（Shortest Time-to-Completion First）

抢占式的 SJF，完全即时地考虑了护航效应。

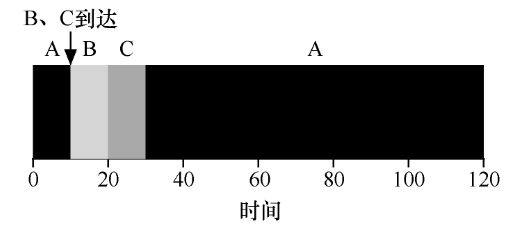
假设 a 进程先到达，b c 进程陆续同时到达，且运行时间已知，分别为 a b c。

平均周转时间 = [ a + ( a + b ) + ( a + b + c ) ] / 3 = ( 3a + 2b + c ) / 3

平均响应时间 = [ 0 + a + ( a + b ) ] / 3 = ( 2a + b ) / 3

对于周转时间来说，若所有工作的周转时间已知，这就是最优化的调度算法了。

不过，我们还有一个调度指标需要讨论，平均响应时间。

平均周转时间和平均响应时间就像鱼与熊掌，二者不可得兼，下面我们来看一下针对平均响应时间做出优化的**轮转（Round-Robin）**策略。

优化平均响应时间

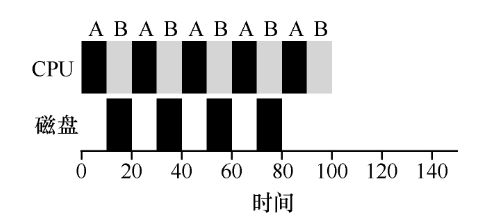
轮转（RR）

称轮转或轮询均可。

轮转是一种公平的策略，它在一个时间片（time slice）（或称调度量子（scheduling quantum））内运行一个工作，在下一个时间片内切换到队列中的下一个工作，如此循环往复，直到所有任务结束。

设一个时间片为 t，a b c 同时陆续到达，且运行时间已知，分别为 a b c。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4OUVBKmF-1610107587742)(C:\Users\10199\AppData\Roaming\Typora\typora-user-images\image-20210107155028268.png)]

平均周转时间 = [ (a + b + c ) + t + ( a + b + c ) + ( a + b + c ) - t ] / 3 = a + b + c

平均响应时间 = [ 0 + t + 2t ] / 3 = t

在这种公平的策略下，任何进程都有机会很快得到响应，平均响应时间相当理想，但平均周转时间却是所有任务运行时间之和，表现非常糟糕，甚至比 FIFO 还差。实际上，任何公平的策略都会带来周转时间的表现欠佳，鱼与熊掌不可兼得。

此外，切换上下文的操作同样需要一定的开销，过于频繁的切换会带来不必要的性能损失，合理地延长时间片，以便摊销上下文切换成本，且保证系统及时响应。

不过，不断切换上下文绝对是一个明智的抉择，缩短响应时间让操作者更加精确地把握机器状态，提高系统的利用率（让人心情愉悦）。

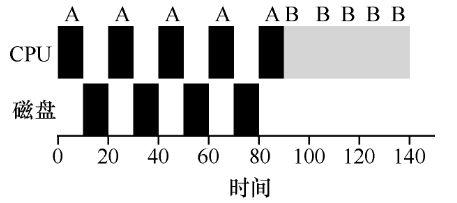
RR 的思想还有一个好处，就是在结合 I/O 时提高对 CPU 的利用率。

在某进程等待 I/O 设备时让另一进程抢占 CPU。

多级反馈队列（MLFQ）

刚才讨论的调度策略都基于一个理想的大前提 —— 操作系统精准地了解每个工作的长度。事实上操作系统对这一点知之甚少。

所以我们接下来要讨论的，就是：

"如何设计一个具有预知能力的调度程序，来逼近 SJF、PSJF 在平均周转时间上的优秀表现？"

我们还要结合 RR，获得不错的平均响应时间。

简述

多级反馈队列（Multi-level Feedback Queue）

该策略拥有一系列队列，每个队列可以拥有多个工作，不同队列具有不同的优先级。

然后，调度程序总是轮转执行高优先级队列中的任务。

由于我们要达到 PSJF 的效果，在 PSJF 中，短工作是要被优先执行的。相应地，在 MLFQ 中，优先级高的工作将被优先执行，这也就意味着优先级高的工作被操作系统视为短工作，即某个进程优先级越高，它的历史表现就越接近短工作的行为。

既然如此，那么我们如何预测一个工作的行为，从而决定他的优先级呢？

其基本思想是，当一个工作进入操作系统时，我们假设其是短工作、或 I/O 密集型（交互型）工作，赋予其最高优先级。如果确实是短工作，则很快会执行完毕，否则可能是长工作、或 CPU 密集型工作，它将被逐步移到较低的优先级队列中。

规则

在 MLFQ 中，进程的优先级并不是一成不变的，调度程序根据几个规则，在实时不断地调整着各个工作的优先级。

我们首先假定一个工作是短的，交互型的工作。

规则一：工作进入操作系统时，放在最高优先级队列中。

如果这个工作执行时间太长，那么他很可能是一个用时较长的 CPU 密集型工作，所以有规则二。

规则二：一旦工作用完了在某一优先级中的时间额度，就降低一级优先级。

如果短的、交互型的工作源源不断，CPU 的资源被大量占用，这时候我们也希望长工作也能被较公平地对待。

或者，若长工作在一段时间内变为交互型工作，我们理应更加公平地对待它。于是我们需要适时提升优先级，所以有规则三。

规则三：经过一段约定好的时间，就将所有工作全部移至最高优先级队列中。

当然，添加时间段 S导致了明显的问题：S的值应该如何设置？德高望重的系统研究员 John Ousterhout 曾将这种值称为“巫毒常量（voo-doo constant）”，因为似乎需要一些黑魔法才能正确设置。如果 S 设置得太高，长工作会饥饿；如果设置得太低，交互型工作又得不到合适的 CPU 时间比例。

实现细节

MLFQ 的很多细节并未给出，例如：

• 队列数量
• 各队列的时间片长度
• 全体提升优先级的间隔

这些细节并没有最优解，基于 MLFQ 思想的具体实现有很多，各自都有各自的特点。

作业中的实现细节

当工作 I/O 结束后应该直接抢占 CPU 吗？

是否抢占对平均周转周期几乎没影响（但可能会改变周转周期），对平均响应周期有一定影响。

因为，当交互型工作不断抢占 CPU 时，后到达的工作将很难被执行。

比例份额

简述

比例份额（proportional-share）或称公平份额（fair-share）

其目标并非优化周转时间和响应时间，而是确保每个工作得到给定比例的 CPU 时间。

彩票调度（lottery scheduling）

彩票调度是比例份额策略的一个实现，其基本思想就是，通过抽奖来决定接下来切换到的进程。

每个进程持有一定数量的券（ticket）（书上翻译为彩票，我认为并不准确），通过每个进程持有的券在所有券中占比来确定该进程的份额。在每个时间片结束后，调度程序通过随机数确定接下来要运行的进程。

每个进程占用的 CPU 资源依概率收敛于其持有的份额。

彩票机制

• 彩票货币（ticket currency）

  用户持有一定数量的货币，货币可以分配给用户下的进程，操作系统将会根据每个用户持有货币的比例，对进程持有的货币兑换为券。

• 彩票转让（ticket transfer）

  一个进程可以临时将自己的券交给另一个进程，以增加其份额。

• 彩票通胀（ticket inflation）

  在进程间相互信任的环境中，一个进程可以临时提升、降低自己持有券的数量。

如何确定份额

该策略的目的并非要解决分配的问题，份额的分配可以人为规定。

例如在超算中，分配给某个用户以固定的 CPU 资源是合情合理的。

实现

抽奖：

// counter: used to track if we’ve found the winner yet
int counter = 0;

// winner: use some call to a random number generator to
//         get a value, between 0 and the total # of tickets
int winner = getrandom(0, totaltickets);

// current: use this to walk through the list of jobs
node_t *current = head;
while (current) {
     
    counter = counter + current->tickets;
    if (counter > winner)
        break; // found the winner
    current = current->next;
}
// ’current’ is the winner: schedule it...

另外，在运行时间不是很长的情况下，抽奖的随机性似乎并不一定公平。

于是出现了一个保证公平的调度算法 —— 步长调度。

步长调度（stride scheduling）

基本思想：根据每个进程所持有的券计算出其步长，例如持有券数量分别为 1 和 2 的两个进程的步长分别为 2 和 1。进程每得到一个时间片的 CPU 资源，其行程值累计一个步长。只要保证每次调度的进程的行程值应不大于其他进程，那么这种调度方式就是公平的。

书上说，若中途到达一个进程，该进程的行程值不好确定，于是该方式不好实现。

我认为我们可以这样实现：

由于所有进程的行程值总是周期性地保持一致。当保持一致时，行程值全部清零，然后将中途到达的进程加入并设置行程值为零，然后重新计算比例份额和步长值。

我这种方法存在的问题在于，行程值全部清零这一操作具有相当的开销。

换个思路，当保持一致时，将中途到达的进程加入，并设置行程值与当前保持一致的行程值相同，当用于保存行程值的内存空间将要溢出时再清零。