优化设计课程设计
Part 1.摘要
本课程设计基于Python语言与C语言实现题目算法，按照课程要求设计题目的算法并实现程序运行，达到了在题目所设情景下实现优化设计的目的。
Part 2.绘制函数图像与求极值问题
2.1绘制函数图像
(1)Python语言作为脚本语言，具有丰富的图像函数库，首先以∆x=1作为单位间隔,考虑到Python集成编译环境IDLE的计算能力，截取x1，x2∈[-20,20]时的函数图像、等值线作为绘图结果。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
N=20
fig=plt.figure()
ax=Axes3D(fig) #生成一个3d对象
X1=np.arange(-N,N,0.2)
X2=np.arange(-N,N,0.2)
X1,X2=np.meshgrid(X1,X2) # 对X1,X2数组进行扩充
print("请选择函数：1.f1(x) 2.f2(x) 3.f3(x)")
choice=int(input())
if choice==1:
Fx=3*X1*X1+2*X1*X2+X2*X2
elif choice==2:
Fx=5*X1*X1+4*X1*X2+8*X2*X2-32*X1-56*X2
else:
Fx=X1*X1*X1-X2*X2*X2+3*X1*X1+2*X2*X2-9*X1
ax.set_xlabel('X1 label', color='blue') #设置X1坐标
ax.set_ylabel('X2 label', color='blue') #设置X2坐标
ax.set_zlabel('Fx label')
ax.plot_surface(X1,X2,Fx,rstride=1,cstride=1,cmap=plt.cm.hot) #生成一个曲面
#ax.contourf(X1,X2,Fx,offset=2,alpha=0.75,cmap=plt.cm.hot) #为等高线填充颜色
ax.contour(X1,X2,Fx,offset=-2,colors='black') #生成等高线 offset参数是等高线所处的位置
plt.show()
运行结果：
定义题目中的三个函数由上至下分别为
, 用户按界面提示选择函数(如图2.1.0所示),分别选择三种函数后，得到的函数图像，点击图2.1.0下方的文件保存图标即可保存完整图像，分别如图2.1.1、图2.1.2、图2.1.3所示。
2.2 C语言求解函数极值
由于计算繁杂，本部分题解算法采用C语言实现：
2.1所截取的函数图像范围不一定包含极小值点，因此在未知三种函数极小值点对应的x1，x2所属范围的情况下，应扩大计算范围，分别取x1，x2∈[-100,100]、x1，x2∈[-200,200]，最小单位∆x=0.01，经检验，在以上两个范围内计算出的三个函数极值点均一致，因此，极值点计算准确。由于计算量极大，使用脚本语言运行时间久，因此采用C语言实现极小值计算。由于数组下标值均大于或等于0，且均为整型值，因此数组中的1个单位代表x1，x2坐标0.01的间距，计算x1，x2∈[-200,200]范围时，以数组Fx[0][0]代表 x1，x2坐标(-200,-200)对应的函数值，以数组Fx[19999][19999]代表 x1，x2坐标(0，0)对应的函数值，以数组Fx[39999][39999]代表 x1，x2坐标(200, 200)对应的函数值。
算法设计：初始化最小值
= Fx[0][0]，基于双重for循环遍历x1，x2坐标范围，依次调用函数F计算每个(x1，x2)对应的
值，若该次循环所求得的<
，则令==X2，并标记对应的x1，x2坐标：x1min=x1，x2min=x2。通过这种迭代计算机制，遍历结束后得到函数极小值。
#include
#define N 40000
float Fx[N][N];
float F(float X1,float X2);//计算Fx值的函数
int choice=0;//用户选择的函数代号
int main(){
float X1,X2,X1_min,X2_min,Fx_min;
printf("请选择：1.f1(x) 2.f2(x) 3.f3(x)\n");
scanf("%d",&choice);
Fx_min=Fx[0][0];//初始化Fx
for(int i=0;i 运行结果：
(1). 
极小值为0，对应对应的x1，x2坐标为(0,0):
(2). 
极小值为-116，对应对应的x1，x2坐标为(2,3):
(3). 
极小值为-1919797，对应对应的x1，x2坐标为(-100,99):
Part 3.线性规划问题及其应用
本章节首先介绍Python处理线性规划问题的方法，详解题目3、题目5的解题思路，并基于Python语言实现解题过程的算法设计。
3.1解题方法与步骤
在Python中导入numpy和scipy库，通过函数array()定义z、A、b矩阵,z为线性规划矩阵式，A、b为线性不等式约束矩阵，G、h矩阵为等式线性约束矩阵，调用optimize.linprog函数并以“optimize.linprog(z,A,b)”的格式传入实参，通过print()语句将其输出即可求出规划所得x值与规划结果。
3.2题目3
from scipy import optimize
import numpy as np
#确定c,A,b
c = np.array([-7,-5])
A = np.array([[3,2],[4,6],[0,7],[-1,-1]])
b = np.array([360,220,230,0])
#求解
res = optimize.linprog(c,A,b) #计算极小值
print(res) #输出极小值运行结果：
3.3题目5
from scipy import optimize
import numpy as np
#定义c,A,b
c=np.array([13,9,10,11,12,8])
A=np.array([[-1.0,0.0,0.0,-1.0,0.0,0.0],[0.0,-1.0,0.0,0.0,-1.0,0.0],[0.0,0.0,-1.0,0.0,0.0,-1.0],
[0.0,0.0,0.0,0.4,1.2,1.0],[0.6,1.2,1.1,0.0,0.0,0.0]])
b=np.array([-400.0,-600.0,-500.0,600.0,900.0])
res = optimize.linprog(c,A,b) #通过optimize函数计算极小值
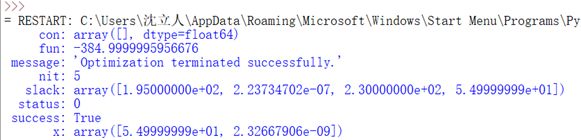
print(res) #输出规划结果运行结果：
Part 4.二次规划问题及其应用
本章节首先介绍Python处理二次规划问题的方法，详解题目2、题目4解题思路，并实现解题过程的算法设计。
4.1·Python解决规划问题的方法
二次规划指带有二次型目标函数和约束条件的最优化问题，其标准形式如下：
在Python中导入cvxopt库，通过matrix函数分别求出P、q、G、h、A、b矩阵，P、q为目标函数矩阵式，G、h为线性不等式约束矩阵，A、b矩阵为等式线性约束矩阵,调用solvers.qp函数并以“solvers.qp(P,q,G,h)”的格式传入实参，sol['x']即为规划所得的到的x值，sol['primal objective']即为规划结果，可通过print()语句将x值与规划结果输出。
而对于MALTLAB，一般用A、b等字母表示参数值的线性不等式约束矩阵，对于参数值的等式线性约束，往往在字母后面加上“eq”，即“equal”表示，如Aeq、Beq矩阵。同时，MATLAB提供ub、lb矩阵控制上、下限值的矩阵，此功能也可用上述线性不等式矩阵实现。
在解决本课程设计的题目过程中，可以认为，相比于线性规划，二次规划增加了一个求偏导数的的解题步骤。
4.2题目2
from cvxopt import matrix, solvers
from scipy import optimize
import numpy as np
P=matrix(np.array([[2.0,-2.0],[-2.0,4.0]]))
q=matrix(np.array([-2.0,-6.0]))
G=matrix(np.array([[1.0,1.0],[-1.0,2.0],[-1.0,0.0],[0.0,-1.0]]))
h=matrix(np.array([2.0,2.0,0.0,0.0]))
sol=solvers.qp(P,q,G,h) #调用优化函数solvers.qp求解
print("x1,x2:\n",sol['x']) #输出x1,x2
print("minf(x):",sol['primal objective']) #输出规划结果运行结果：
4.3题目4
from cvxopt import matrix, solvers
from scipy import optimize
import numpy as np
P=matrix(np.array([[1.0,-1.0],[-1.0,2.0]]))
q=matrix(np.array([-2.0,-6.0]))
G=matrix(np.array([[1.0,1.0],[-1.0,2.0],[2.0,2.0],[-1.0,0.0],[0.0,-1.0]]))
h=matrix(np.array([2.0,2.0,3.0,0.0,0.0]))
sol=solvers.qp(P,q,G,h) #调用优化函数solvers.qp求解
print("x1,x2:\n",sol['x']) #输出x1,x2
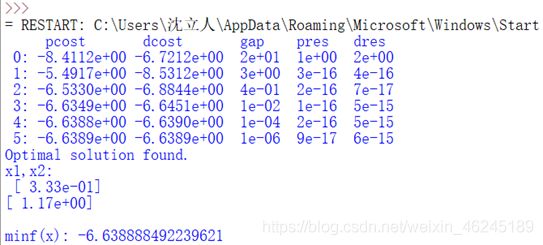
print("minf(x):",sol['primal objective']) #输出规划结果运行结果：
最后，感谢观看，如有内容错误，欢迎指正。喜欢的小伙伴记得三连哟~