西瓜书读书笔记——第五章:神经网络
西瓜书读书笔记——第五章:神经网络
- 5.1 神经元模型
- 5.2 感知机与多层网络
-
- 5.2.1 感知机
- 5.3 误差逆传播算法
- 5.4 全局最小与局部极小
- 5.5 深度学习
5.1 神经元模型
在生物神经网络中,每个神经元与其他神经元相连,当某个神经元兴奋时,它就会向其他相连的神经元传递化学物质,从而改变了这些神经元内的电位;如果某个神经元的电位超过了一个阈值(threshold),那么就会被激活,即兴奋起来,向其他神经元发送化学物质。
M-P神经元模型正是从生物神经网络中抽象出来的。
在M-P神经元模型中,神经元接收到其他n个神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元收到的总输入值将与神经元的阈值进行比较,然后通过激活函数(active function)处理以产生神经元的输出。
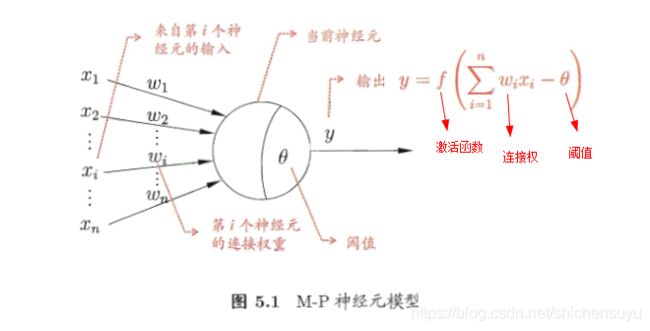
把许多这样的神经元按一定的层次结构连接起来,就得到了神经网络。
神经网络可视为一个包含很多参数的数学模型,这个模型是若干个函数相互嵌套代入而得。有效的神经网络大多以数学证明为支撑。
关于激活函数的选择,理想的激活函数是如下图所示的阶跃函数,它将输入值映射为“0”(神经元抑制),“1”(神经元兴奋)。
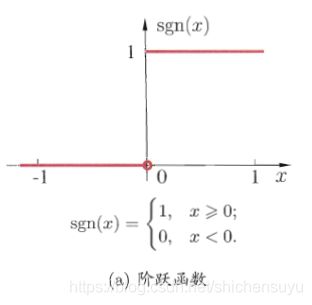
注:阶跃函数是单位阶跃函数的变体,单位阶跃函数在x=0时取值为0.5
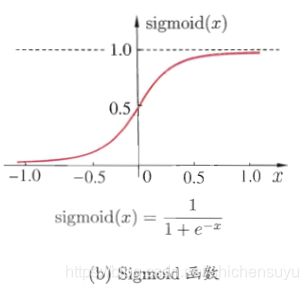
但是,阶跃函数具有不连续不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数。如下图所示,它把可能在较大范围内变化的输入值挤压到(0,1)输出值的范围内,因此有时也称为挤压函数(squashing function)
5.2 感知机与多层网络
5.2.1 感知机
感知机(Perceptron)由两层神经元组成,输入层接受外界输入信号后传递给输出层,输出层是M-P神经元(也称:阈值逻辑单元(threshold logic unit)),为二类分类的线性分类模型(激活函数为阶跃函数)。
感知机的学习规则:
对于训练样本(x,y),当该样本进入感知机学习后,会产生一个对应的输出值 y ^ \widehat y y ,若真实输出值y与其不一致,则感知机会对权重进行调整,若激活函数为阶跃函数,则调整方法为(基于梯度下降):

感知机学习过程:
可以看出感知机是通过逐个样本输入来更新权重:
\quad 设定好权重(一般为随机),逐个地输入样本数据,若输出值与真实标记一致则继续输入下一个样本,否则更新权重,再开始重新逐个检验,直到所有的样本的输出值与真实标记一致。
感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元,其学习能力非常有限,只能处理线性可分的问题。
- 对于线性可分的问题,感知机的学习过程总能收敛而求得适当的权向量 w = ( w 1 ; w 2 ; . . . ; w n + 1 ) w=(w_1;w_2;...;w_{n+1}) w=(w1;w2;...;wn+1),即感知机模型总能将训练数据(不是测试数据)的每一个样本都预测正确,但也容易产生过拟合问题。
- 对于线性不可分的问题(如异或问题),则需要用多层功能神经元。
考虑到现实任务的复杂性,更一般的,常见的神经网络是如下图所示的层级结构,每层神经元与下层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接,这样的神经网络结构通常称为“多层前馈神经网络”(multi-layer feedforward neural networks)。

- 输出层:输出层神经元为功能神经元,进行函数处理
- 隐层(hidden layer):隐层神经元为功能神经元,进行函数处理
- 输入层:输入层神经元仅接收外界输入信息,不进行函数处理
神经网络的学习过程就是:根据训练数据来调整神经元之间的连接权和每个功能神经元的阈值。
5.3 误差逆传播算法
多层网络拥有比感知机更强大的学习能力,之前论述的感知机学习规则对于多层网络来说显然不够用,需要更强大的学习算法,误差逆传播(error BackPropagation,简称BP)算法就是其中的杰出代表,是迄今最成功的神经网络学习算法。
BP算法除了运用在多层前馈神经网络之外,还可以用在许多其他类型的神经网络,例如训练递归神经网络等等。
给定训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } , x i ∈ R d , y i ∈ R l D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\},x_i\in\R^d,y_i\in \R^l D={ (x1,y1),(x2,y2),...,(xm,ym)},xi∈Rd,yi∈Rl
即:输入示例由 d d d个属性描述,输出 l l l维实值向量
下图给出了一个拥有 d d d个输入神经元, l l l个输出神经元, q q q个隐层神经元的多层前馈神经网络。其中,
θ j \theta_j θj:输出层第 j j j个神经元的阈值
γ h \gamma_h γh:隐层第h个神经元的阈值
υ i h \upsilon_{ih} υih:输入层第 i i i个神经元与隐层第 h h h个神经元之间的连接权重
ω h j \omega_{hj} ωhj:隐层第 h h h个神经元与输出层第 j j j个神经元之间的连接权重
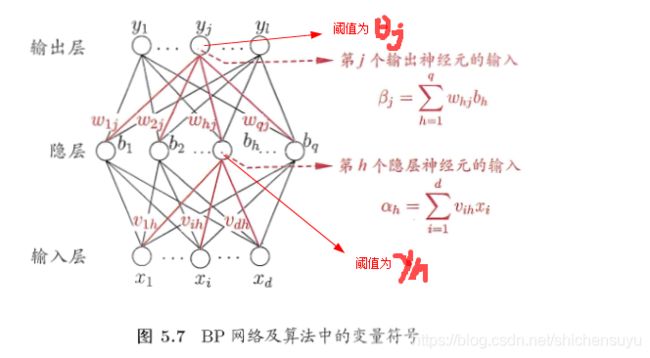
α h \alpha_h αh:第 h h h个隐层神经元接收到的输入
β j \beta_j βj:第 j j j个输出神经元的输入
假设功能神经元的激活函数都为対率函数( y = 1 1 + e − x y=\dfrac{1}{1+e^{-x}} y=1+e−x1)
l l l个输出层的神经元对应输出的即为一个 l l l维的实值向量 y ^ \widehat y y
对于训练例 ( x k , y k ) (x_k,y_k) (xk,yk),假定神经网络的输出为 l l l维实值向量 y ^ k = ( y ^ 1 k , y ^ 2 k , . . . , y ^ l k ) \widehat y_k=(\widehat y_1^k,\widehat y_2^k,...,\widehat y_l^k) y k=(y 1k,y 2k,...,y lk),即
(5.3) y ^ j k = f ( β j − θ j ) \widehat y_j^k=f(\beta_j - \theta_j)\tag{5.3} y jk=f(βj−θj)(5.3)
则网络在训练例 ( x k , y k ) (x_k,y_k) (xk,yk)上的均方误差 E k E_k Ek为:
(5.4) E k = ∑ j = 1 l 1 2 ( y j k − y ^ j k ) 2 E_k=\sum_{j=1}^l\dfrac{1}{2}(y_j^k-\widehat y_j^k)^2\tag{5.4} Ek=j=1∑l21(yjk−y jk)2(5.4)
图5.7的网络中有 ( d + 1 + l ) ∗ q + l (d+1+l)*q+l (d+1+l)∗q+l个参数需要确定:
- d ∗ q d*q d∗q个输入层与隐层神经元的所有连接权
- l ∗ q l*q l∗q个隐层与输出层神经元的所有连接权
- q q q个隐层神经元的阈值
- l l l个输出层神经元的阈值
BP是一个迭代学习算法,在迭代的每一轮采用广义的感知机学习规则对参数进行更新估计,与感知机的类似,对于任意参数 v v v,更新估计式为:
v ← v + Δ v v\leftarrow v+\Delta v v←v+Δv
基于梯度下降策略寻找最小化均方误差,负的梯度方向为最速下降方向,以下是对各个参数更新公式的推导:

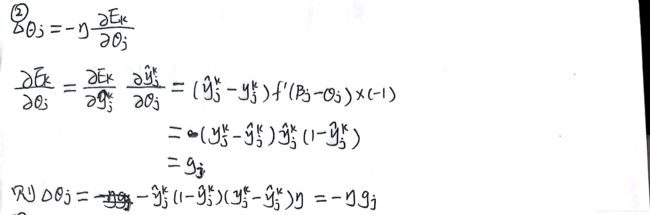
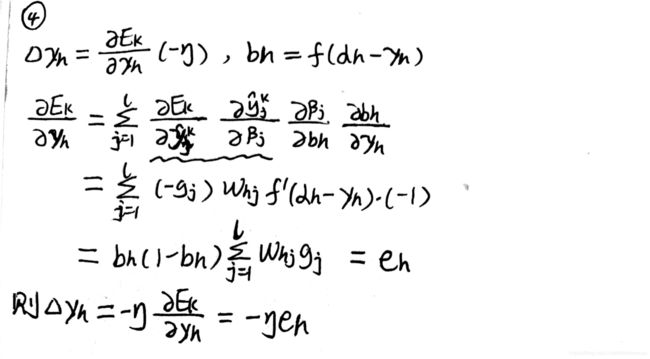
注:
- g i g_i gi为输出层神经元梯度项
- e h e_h eh为隐层神经元梯度项
学习率 η ∈ ( 0 , 1 ) \eta \in(0,1) η∈(0,1)控制着算法每一轮迭代中更新的步长(一般设置为0.1):
- η \eta η太大则容易振荡
- η \eta η太小则收敛速度过慢
故有时为了精细调节,可令 Δ θ j 和 Δ w h j \Delta \theta_j和\Delta w_{hj} Δθj和Δwhj使用 η 1 \eta_1 η1,令 Δ γ h 和 Δ v i h \Delta \gamma_h和\Delta v_{ih} Δγh和Δvih使用 η 2 \eta_2 η2,两者未必相等
以下是BP算法的工作流程:
- 从repeat循环和for循环可以看出,一旦某个样例 ( x k , y k ) (x_k,y_k) (xk,yk)使得各参数做出更新,则需开始新一轮迭代,重新从 y 1 y_1 y1开始又逐次进行检验更新
- 具体的数据流过程为:输入示例传给输入层,再逐层将信号前传,直到产生输出层的结果,然后计算输出层的误差(第4-5行),再将误差逆传播至隐层神经元(第6行),最后根据隐层神经元的误差来对连接权和阈值进行调整(第7行)。
- 停止条件,如训练误差达到了某个很小的值,它应该与缓解BP过拟合的策略有关。
BP算法的目标是要最小化训练集 D D D上的累积误差 E E E:
(5.16) E = 1 m ∑ k = 1 m E k E=\dfrac{1}{m}\sum_{k=1}^mE_k\tag{5.16} E=m1k=1∑mEk(5.16)
上图的更新规则是基于for循环下的单个 E k E_k Ek而进行的(但最终效果依然是最小化累积误差),若类似地推导出基于累积误差最小化的更新规则(即每次都是基于累计误差而不再是单个误差进行调整),就得到了累积误差逆传播算法。
- 标准BP算法:
- 每次更新只针对单个样例,参数更新非常频繁
- 对应不同样例而进行的参数更新可能会产生“抵消”的效果
- 为了达到同样的累计误差极小点,往往需进行更多次的迭代
- 累计BP算法:
- 直接针对累计误差最小化,读取整个训练集 D D D一遍后(进行了一轮学习)才进行参数更新,参数更新频率相对低得多
- 累计误差下降到一定程度后,进一步下降会非常缓慢
- 相对更慢获得较好的解,尤其是在训练集 D D D很大的时候,标准BP算法比累积BP算法明显更快求得较好的解
注:标准BP算法和累积BP算法的区别类似于随机梯度下降与标准梯度下降之间的区别
梯度下降和随机梯度下降之间的关键区别:
1、标准梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查某个训练样例来更新的。
2、在标准梯度下降中,权值更新的每一步对多个样例求和,需要更多的计算。
3、标准梯度下降,由于使用真正的梯度,标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长。
4、如果标准误差曲面有多个局部极小值,随机梯度下降有时可能避免陷入这些局部极小值中。
BP神经网络过拟合的缓解方法:
\quad 多层前馈神经网络有强大的表示能力,只要隐层包含的神经元数量足够多,它就能以任意精度逼近任意复杂度的连续函数。
但是,如何设置隐层神经元的个数仍是个未决问题,实际应用中通常靠“试错法”(trail-by-error)调整
由于多层前馈网络的强大表示能力,经常遇到这样的情况:训练误差持续降低,但测试误差却在上升,这就是BP神经网络经常遭遇的过拟合问题。
通常,有以下两种方法缓解BP网络的过拟合:
- “早停(early stopping)”:将数据分成训练集和验证集,训练集用来计算梯度,更新连接权和阈值,验证集用来估计误差。若出现上文所述的过拟合现象,则停止训练,同时返回具有最小验证集误差的连接权和阈值。
- “正则化(regularization)”:在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权和阈值的平方和。仍令 E k E_k Ek表示第 k k k个训练样例上的误差, w i w_i wi表示连接权和阈值,则误差目标函数(5.16)改变为:
(5.17) E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 E=\lambda \dfrac{1}{m}\sum_{k=1}^mE_k+(1-\lambda)\sum_i w_i^2\tag{5.17} E=λm1k=1∑mEk+(1−λ)i∑wi2(5.17) 其中, λ ∈ ( 0 , 1 ) \lambda\in(0,1) λ∈(0,1)用于对经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计。
注:
- 增加连接权与阈值平方和这一项后,训练过程将会偏好比较小的连接权和阈值(目标为最小化误差),使网络输出更加“光滑”(这样理解:较小的连接权和阈值使得计算式参数较小,曲线也更光滑),从而对过拟合有所缓解。
- 式(5.17)可以等价于:
m i n 1 λ E = 1 m ∑ k = 1 m E k + 1 − λ λ ∑ i w i 2 min\quad\dfrac{1}{\lambda}E=\dfrac{1}{m}\sum_{k=1}^mE_k+\dfrac{1-\lambda}{\lambda}\sum_i w_i^2 minλ1E=m1k=1∑mEk+λ1−λi∑wi2
这种形式的函数就是西瓜书第6章支持向量6.4.2 正则化小节提到的正则化问题, 1 − λ λ \dfrac{1-\lambda}{\lambda} λ1−λ就是该正则化问题的正则化常数, 1 m ∑ k = 1 m E k \dfrac{1}{m}\sum_{k=1}^mE_k m1∑k=1mEk为结构风险,用来表示希望获得什么样的模型(这里是误差最小), ∑ i w i 2 \sum_i w_i^2 ∑iwi2为经验风险,用来描述模型与数据的契合程度。
5.4 全局最小与局部极小
之前的讨论得出了误差目标函数,它是关于连接权 ω \omega ω和阈值 θ \theta θ的函数。此时,神经网络的训练过程可看作一个参数寻优过程,即在参数空间中,寻找一组最优参数使得E最小。我们在参数寻优过程中希望找到的就是全局最小值。

显然,参数空间内梯度为零的点,只要其误差函数值小于邻点的误差函数值,就是局部极小值。局部极小值可以有多个,全局最小值只有一个。我们在参数寻优过程中希望找到的就是全局最小值。
那么,如何找到全局最小值呢?
基于梯度的搜索是使用最广泛的参数寻优方法。
在该类方法中,我们从某些初始解出发,然后根据梯度确定搜索方向。例如,由于负梯度是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解。
若误差函数在当前点的梯度为0,则已经达到局部极小,之后不会再做更新,这就意味着参数的迭代更新就到此停止了。很明显这样做的一个问题是,若误差函数有多个局部极小,那么就不能保证当前找到的解是全局最小。这种情况,我们称参数寻优陷入了局部极小。通常,我们采用以下三种策略来试图跳出局部最小,从而进一步接近全局最小(不能保证得到的就是全局最小,只是逼更近):
- 以多组不同的参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数。
注:相当于从多个不同的初始点开始搜索,这样可能陷入多个不同的局部极小,从中进行选择有可能得到更接近全局最小的解。 - 使用随机梯度下降。与标准梯度下降法精确计算精度不同,随机梯度下降在计算梯度时引入了随机因素。于是,即使陷入局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索。
- 使用模拟退火(simulated annealing)技术。
模拟退火的过程:
①:若 f ( Y ( i + 1 ) ) ≤ f ( Y ( i ) ) f(Y(i+1))\leq f(Y(i)) f(Y(i+1))≤f(Y(i)),即移动后得到更优解,则总是接受该移动
②:若 f ( Y ( i + 1 ) ) > f ( Y ( i ) ) f(Y(i+1))> f(Y(i)) f(Y(i+1))>f(Y(i)),即移动后得到更差解,则以一定的概率 t t t接受移动, t t t随着时间的推移逐渐降低(才能最终趋于稳定)。
如下图中,从A移到B的过程就是上面的①,总是接受该移动;从B移到BC之间的峰值处时,就是上面的②,每次右移的概率都在减小。如果这个坡特别长,那么很有可能最终没有翻过这个坡。如果坡不长,则很有可能翻过,即跳出了局部极小,这取决于 t 和 Δ t t和\Delta t t和Δt的设定。
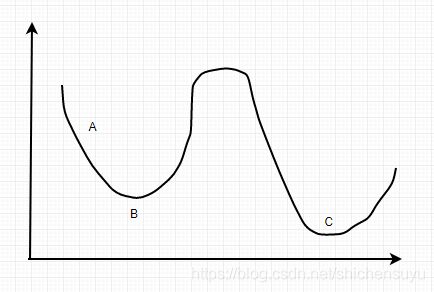
从上面三种策略的描述可以看出,它们都只是一种启发式的方法,只能更逼近全局最小而不能保证得到的就是全局最小。
除了以上三种策略之外,遗传算法也经常用来训练神经网络以更好地逼近全局最小。
注:推荐一篇个人觉得写得比较好的遗传算法的文章https://blog.csdn.net/qq_31805821/article/details/79763326
5.5 深度学习
理论上,参数越多的模型复杂度越高,容量越大,能完成更复杂的任务。但一般情况下,复杂模型的训练效率低,易陷入过拟合。训练效率低可由算力的提升解决,过拟合可由数据规模的增大有所缓解。因此,以深度学习为代表的复杂模型开始受到关注。
对于神经网络模型,提高容量的一个简单方法就是增加隐层的数量。
从增加模型复杂度的角度看,增加隐层的数目显然比增加隐层神经元的数目更有效。因为增加隐层数不仅增加了拥有激活函数的神经元数目,还增加了激活函数嵌套的层数。
多隐层神经网络难以直接用经典算法(如标准BP算法)进行训练,因为误差在多隐层内逆传播往往会发散而不能收敛。
无监督逐层训练(unsupervised layer-wise training)是多隐层神经网的训练的有效手段。其基本思想是:
- 每次训练一层隐结点,训练时将上一层隐结点 的输出作为输入,而本层隐结点的输出又作为下一层隐结点的输入,这称为“预训练”(pre-training)
- 预训练全部完成后,再对整个网络进行微调(fine-tuning)训练
预训练+微调的做法可视为:对每组先找到局部看起来比较好的设置,然后再基于这些局部较优的结果联合起来进行全局寻优。
这样就在利用模型大量参数所提供的自由度的同时,有效地节省了训练开销。
还有一种节省训练开销的策略是权共享(weight sharing),即让一组神经元使用相同的连接权。这种策略在卷积神经网络(CNN)中发挥了重要作用。
