【李宏毅机器学习笔记】1、回归问题(Regression)
【李宏毅机器学习笔记】1、回归问题(Regression)
【李宏毅机器学习笔记】2、error产生自哪里?
【李宏毅机器学习笔记】3、gradient descent
【李宏毅机器学习笔记】4、Classification
【李宏毅机器学习笔记】5、Logistic Regression
【李宏毅机器学习笔记】6、简短介绍Deep Learning
【李宏毅机器学习笔记】7、反向传播(Backpropagation)
【李宏毅机器学习笔记】8、Tips for Training DNN
【李宏毅机器学习笔记】9、Convolutional Neural Network(CNN)
【李宏毅机器学习笔记】10、Why deep?(待填坑)
【李宏毅机器学习笔记】11、 Semi-supervised
【李宏毅机器学习笔记】 12、Unsupervised Learning - Linear Methods
【李宏毅机器学习笔记】 13、Unsupervised Learning - Word Embedding(待填坑)
【李宏毅机器学习笔记】 14、Unsupervised Learning - Neighbor Embedding(待填坑)
【李宏毅机器学习笔记】 15、Unsupervised Learning - Auto-encoder(待填坑)
【李宏毅机器学习笔记】 16、Unsupervised Learning - Deep Generative Model(待填坑)
【李宏毅机器学习笔记】 17、迁移学习(Transfer Learning)
【李宏毅机器学习笔记】 18、支持向量机(Support Vector Machine,SVM)
【李宏毅机器学习笔记】 19、Structured Learning - Introduction(待填坑)
【李宏毅机器学习笔记】 20、Structured Learning - Linear Model(待填坑)
【李宏毅机器学习笔记】 21、Structured Learning - Structured SVM(待填坑)
【李宏毅机器学习笔记】 22、Structured Learning - Sequence Labeling(待填坑)
【李宏毅机器学习笔记】 23、循环神经网络(Recurrent Neural Network,RNN)
【李宏毅机器学习笔记】 24、集成学习(Ensemble)
------------------------------------------------------------------------------------------------------
【李宏毅深度强化学习】视频地址:https://www.bilibili.com/video/av10590361?p=3
课件地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html
-------------------------------------------------------------------------------------------------------
Introduction
在现实中,有很多事情可以应用regression来求解。比如上图的情况。
计算神奇宝贝CP值为例子
![]()
具体以一个例子,这个例子是预测神奇宝贝的CP值(战力值)。这里函数的输入就是神奇宝贝进化前的信息,输出就是这只神奇宝贝进化后的CP值。
为了得到一个能实现以上功能的函数,需要进行以下3步:
- 找一个model(function set)
- 评估function set里面的function
- 挑选出最优的function
在这个例子中,可以假设这个function长这样,![]() 。其中w、b都是参数,代入不同的数字会产生无穷个不同的函数
。其中w、b都是参数,代入不同的数字会产生无穷个不同的函数![]() ,
,![]() ,
,![]() ……这些function的集合就是model(function set)。为了找到合适的function(
……这些function的集合就是model(function set)。为了找到合适的function(![]() 就是错误的,不可能进化后CP值减少),需要通过让模型进行训练才能得到最优的function。
就是错误的,不可能进化后CP值减少),需要通过让模型进行训练才能得到最优的function。
这里的model是一个linear model,形如![]() 的也是。
的也是。![]() 称为feature,
称为feature,![]() 称为weight,b称为bias。
称为weight,b称为bias。
![]()
为了能让模型有data可以训练,需要抓来一些神奇宝贝。![]() 代表不同的神奇宝贝,
代表不同的神奇宝贝,![]() \hat代表进化后的实际的CP值。
\hat代表进化后的实际的CP值。
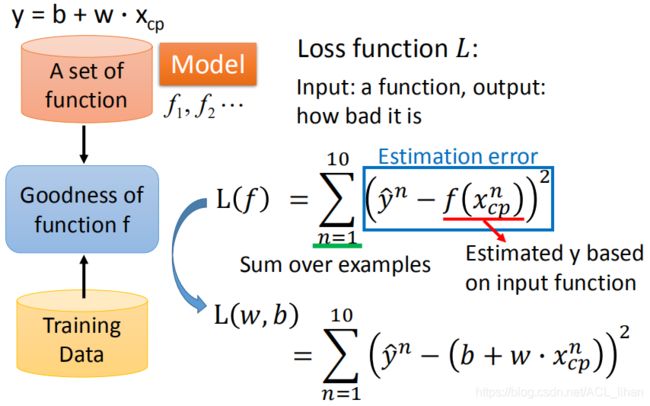
为了从function set里选出最优的function,需要定义一个Loss function ![]() ,这个Loss function的输入是function set的某一个function,输出这个function有多差。
,这个Loss function的输入是function set的某一个function,输出这个function有多差。![]() 输出值越大,说明这个function不好,
输出值越大,说明这个function不好,![]() 输出值越小,说明这个function好,其中,
输出值越小,说明这个function好,其中,![]() \hat代表真实的CP值,
\hat代表真实的CP值,![]() 代表预测出来的CP值,相减后去平方,然后求和(这里假设10只神奇宝贝的data)。
代表预测出来的CP值,相减后去平方,然后求和(这里假设10只神奇宝贝的data)。
由于函数 f 中包含参数w,b,所以![]() 也可以表示为
也可以表示为![]() 。
。
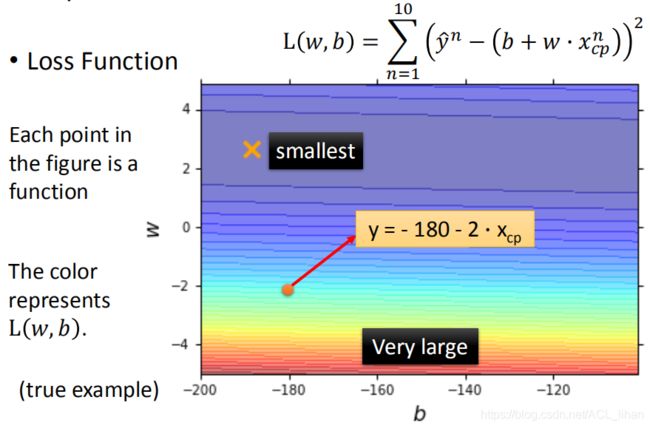
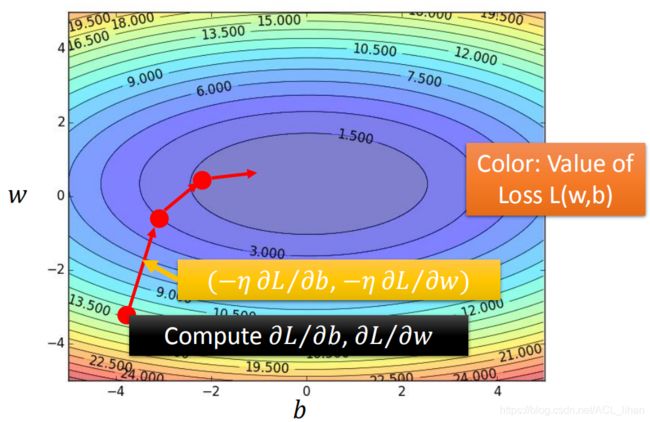
把Loss function的w,b制成图,每个点代表一个function,如图所示。假设蓝色区域是function比较好的,红色区域是function比较不好的。
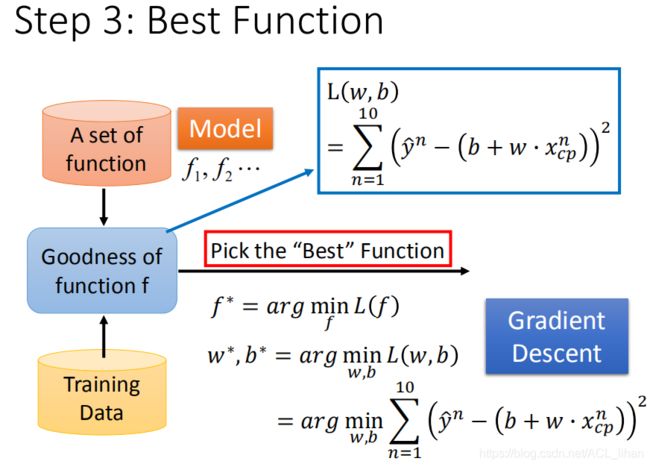
定好Loss function后我们可以衡量每个function的好坏,接下来第3步就要找出哪个function是最好的。
在上一步有了Loss function之后,通过Gradient Descent,不断更新参数w、b,最终找到一个loss值相对较低的function。(Gradient Descent会找到一个局部最优的解,虽然可能不是全局最优,但也还行)
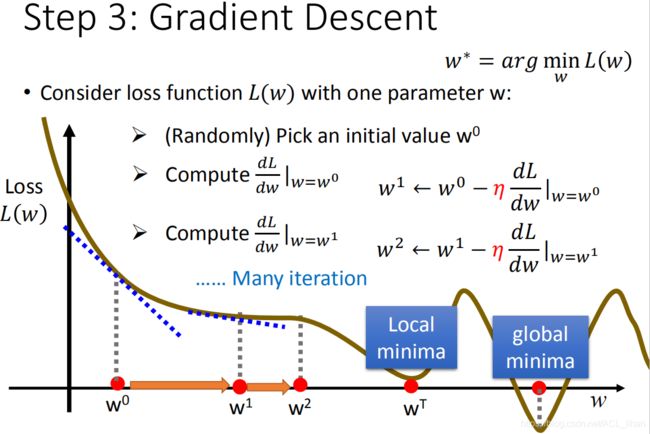
刚才讲到gradient descent,这里具体看一下。 为了找到一个比较好的参数,会进行以下的步骤:
- 随机初始化一个参数
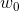
- 计算
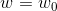 处对
处对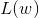 的偏微分(切线斜率)。如果斜率为负,则增大w的数值。如果斜率为正,则减小w的数值。
的偏微分(切线斜率)。如果斜率为负,则增大w的数值。如果斜率为正,则减小w的数值。 - 将参数
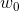 减去
减去  乘上此处的切线斜率,就得出新的参数
乘上此处的切线斜率,就得出新的参数  。(
。( 代表学习率(learning rate),代表参数w每次向左右“跨的步”有多大)
代表学习率(learning rate),代表参数w每次向左右“跨的步”有多大)
重复以上步骤。。。。。
最终会找一个loss值比较小的参数w。这个点可能是local minima而不是global minima,但是也还行。
上图是两个参数的更新参数过程,和上面一个参数的做法类似。只不过这边是求偏微分。
对刚才的过程做一个可视化,蓝色代表loss值较低的区域。红色箭头代表参数更新的过程。
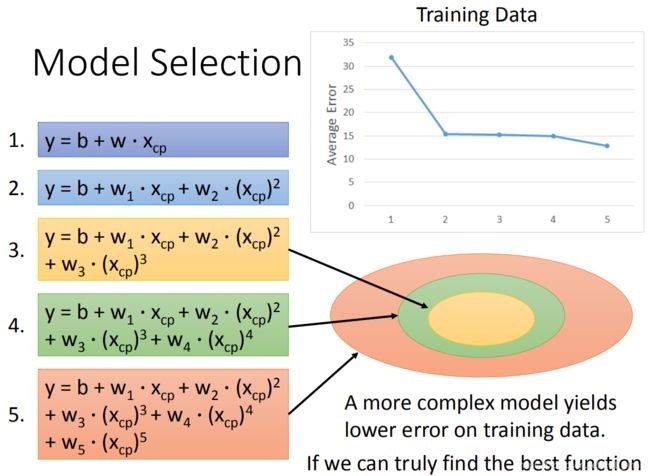
为了实现更低的loss,将刚才的model变得更高次。随着model变得更高次,它能表示的space就越大,所以就越能拟合数据。
可以看到在training data上,随着model的复杂程度的上升,loss值不断降低。但在testing data上是否也如此?
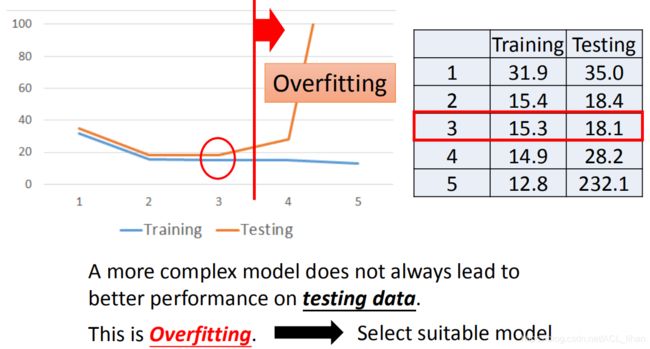
可以看到,当model复杂到一定程度后,在testing data 的loss值反而变得很高。这种在training data上loss值很低,在testing data上loss值很高的情况叫做过拟合(overfitting)。所以还是根据实际问题需要,选择合适的model。
为了实现更低的loss值,可以做以下两个步骤:
1、重新设计model
这里收集了更多神奇宝贝的资料,可以看出CP值的变化和神奇宝贝对应的物种是有关系的。所以需要对上面的model重新修改下。
![]()
通过类似 if 的做法去判断物种,然后不同物种的神奇宝贝有不同的function去计算进化后的CP值。
为了使model还是一个linear model,需要将上面的做法改为以下式子:
通过 ![]() 来实现刚才 if 的功能。比如当
来实现刚才 if 的功能。比如当 ![]() 的时候,
的时候, ![]() 就输出1。下面
就输出1。下面![]() 等等都变成0,所以实现只调这种物种的参数并且仍然是linear model。
等等都变成0,所以实现只调这种物种的参数并且仍然是linear model。
2、Regularization
![]()
给Loss function加上一项regularization,![]() ,我们会希望这一项越小越好,即最终的参数
,我们会希望这一项越小越好,即最终的参数 ![]() 越小越好。
越小越好。
参数 ![]() 越小代表function越平滑(smoother),这样做的好处就是使得函数的输出对于输入的不同data不会太敏感,所以一些noisy的干扰就不会产生太大的影响。
越小代表function越平滑(smoother),这样做的好处就是使得函数的输出对于输入的不同data不会太敏感,所以一些noisy的干扰就不会产生太大的影响。
这里可能会有人想,bias需不需要regularization?答案是不用,因为bias和输入的 x 关系不大。
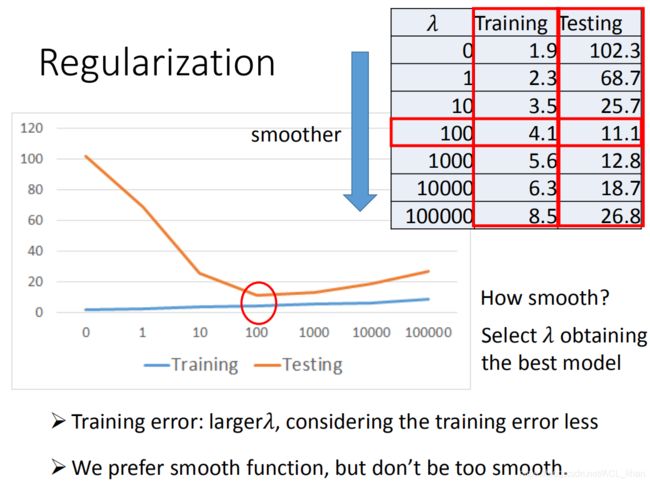
现在的Loss值有两项,一项是和error的大小有关,一项是和function的光滑程度有关。![]() 的值越大,则说明更偏向于考虑function的光滑。
的值越大,则说明更偏向于考虑function的光滑。
从上面的实验结果,可以看出![]() 的值太大的话,会导致function不怎么考虑error的值,所以并不是function越光滑越好。因为当function过于光滑,会导致不管输入是什么,都得到差不多的输出值,这肯定是不对的。
的值太大的话,会导致function不怎么考虑error的值,所以并不是function越光滑越好。因为当function过于光滑,会导致不管输入是什么,都得到差不多的输出值,这肯定是不对的。