【菜鸡刷题 - 并查集专题 1 - leetcode 1579 】alice bob 图完全可遍历 | 并查集 | python
先马一下
太困了,明天要整完这三个大题噢! 2021/1/27 晚 23:59
@author=YHR | 原创不易,转载请注明来源!|
以下都是个人的理解,大家仁者见仁,智者见智,不对的地方大家可以指出来,然后一起讨论~
文章目录
- 基础知识铺垫
-
- 1. 克鲁斯卡尔的简单介绍:
- 2. 引入 并查集 :
- 1579 保证图可完全遍历 -- 由克鲁斯卡尔引入并查集
-
- 题目描述:
- 题目解读:
- 代码分块讲解 (PK规则按每个酋长的孩子数 -- 人多力量大)
- 整体代码:
基础知识铺垫
1. 克鲁斯卡尔的简单介绍:
克鲁斯卡尔独特要求:
最小生成树:最小成本,即: N个顶点,N-1条边,把所有点以最小代价连通起来,边的权值和最小。
.
克鲁斯卡尔算法:每次选择的边依附的起点,终点,必须来自于不同的连通分量 – 避免成环, (怎么判断来自于不同的连通分量呢? – “祖先” 的概念,下文详细介绍。)
- 克鲁斯卡尔特性: 每次选择的边依附的起点,终点,必须来自于不同的连通分量
- 初始化 每个点 可以看作是一个连通分量, N个点,初始有N个连通分量。
- 克鲁斯卡尔每次选中一条边,连通了 起点 & 终点 所属的两个连通分量,则总连通分量数-1。
- 克鲁斯卡尔结束的时候,如果连通分量数目为1,说明整个图只有一个连通分量,则所有的点都被连起来了!
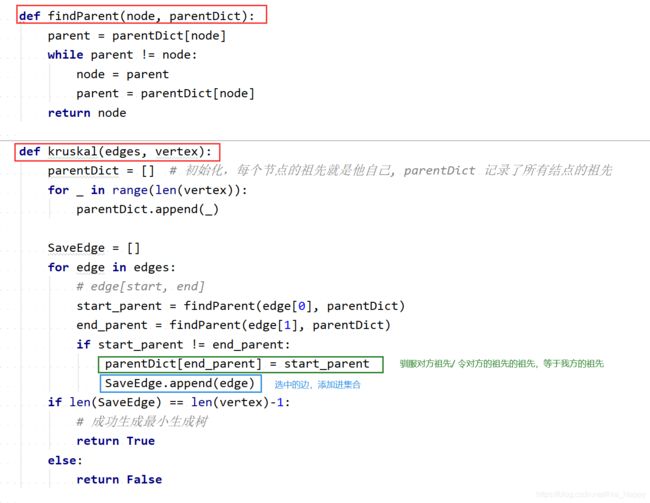
以下是一份克鲁斯卡尔的普通算法版本,与本题无关!
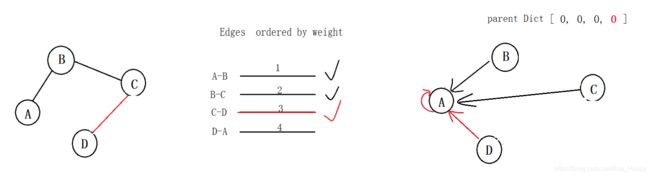
以上 过程 可以用下图来解释:
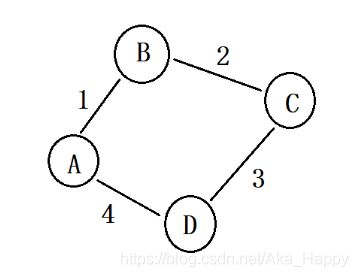
初始生成树,结点之间彼此没有联系,每个节点就是一个连通分量,初始的时候,整个图N个结点,N个连通分量。
如右图,每个结点初始的 祖先 就是他自己。

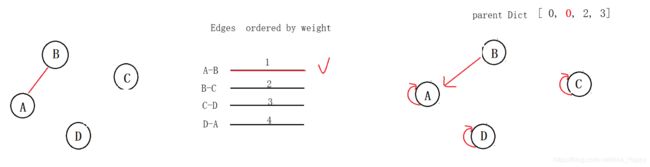
目前最短路径的边就是 A-B,起点是 0(A) 结点, 终点是 1 (B) 结点。
- 根据parent Dict来看,A 结点的父辈是0, 即他自己,而 0的父辈也是0, 即A最终的祖先是 0;
- 同理,发现,B 结点的父辈是1,即他自己,而 1的父辈也是1, 则B最终的祖先是 1,也是自己。
按照代码的逻辑:

A祖先0 != B祖先1, 需要把终点B的祖先的祖先,变成起点A的祖先, 修改 parent Dict。
所以如下图:parent Dict 里, B的祖先1的祖先改成 0 (A)。
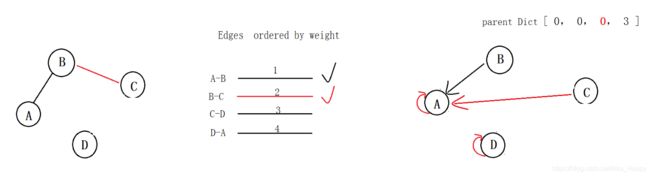
目前最短路径的边就是 B-C,起点是 B (1)结点, 终点是 C(2) 结点。
- 根据parent Dict来看,B(1) 结点的父辈是0,而 0的父辈也是0, 则B最终的祖先是 0。
- 同理,C(2) 结点的父辈是2,而 2的父辈也是2, 则C最终的祖先是 2,即他自己。
按照代码的逻辑,修改 parent Dict,把 终点C 的祖先2的祖先改成 起点B 的祖先0。
B-C 加入 saveEdge数组里。
目前最短路径的边就是 C-D,起点是 C(2)结点, 终点是 D(3) 结点。
- 根据parent Dict来看,C(2) 结点的父辈是0,而 0的父辈也是0, 则C 最终的祖先是 0。
- 同理,D(3) 结点的父辈是3,而 3的父辈也是3, 则D 最终的祖先是 3,即他自己。
按照代码的逻辑,修改 parent Dict,把终点 D 的祖先3的祖先改成 起点C的祖先0。
C-D 加入 saveEdge数组里。
目前最短路径的边就是 D-A,起点是 D(3)结点, 终点是 A(0) 结点。
- 根据parent Dict来看,D(3) 结点的父辈是0,而 0的父辈也是0, 则D 最终的祖先是 0。
- 同理,A(0) 结点的父辈是0,而0的父辈也是0, 则A 最终的祖先是0,即他自己。
发现 起点,终点,的祖先是同一个,说明他俩已经属于同一个连通分量了,已经被连通了,再加入就会成环,所以不允许加入该边。
由此可以发现一个关键问题:
parent Dict 作用 :记录了 一个结点的父辈是谁?由父辈可以顺藤摸瓜得到结点的祖先,即属于哪个 连通分量?
.
祖先的父辈永远是他自己! 即一棵树的根节点!
.
树内每个结点的父亲可能不一样,但他们的最终祖先肯定只有一个 – 那就是根节点。
大家如果还有点不懂的话,可以这么理解:
把结点看成小原始人,每个结点的 父辈 是一个小队长,结点的 祖先 当成整个部落(连通分量)的最高酋长。
.
要找每个结点的祖先,就得从 结点 – 父辈 – 父辈的父辈… 顺藤摸瓜,才能找到祖先,我们的最高酋长。祖先父辈就是他自己。
.
不同部落(不同连通分量)的结点相遇,必要打一架,两个结点号召彼此部落的全部人来PK,
.
谁打输了,输方整个部落(连通分量)都要归顺过去。也就是输方的酋长,变成胜方酋长的下属。
.
也就是,胜方的连通分量,和输方的连通分量 已经连通成一家啦
.
2. 引入 并查集 :
刚才说 克鲁斯卡尔 需要 parent Dict 去判断是否成环,也就是不允许已经连通的两个点,再添加一条边。
但克鲁斯卡尔存边的那些操作在本题里就已经不是必须的啦~
我们只需要取最重要的部分 – 用parent Dict 判断结点所属的连通分量 – 即祖先,
.
也就迎来了我们的并查集:
.
并查集 最重要就是,并 & 查。
-
遇: 两结点(小原始人)因为某种情况(比如存在边,或者其他规则)相遇,
-
查: 查看是不是属于同一部落,用parent Dict 判断,找到彼此的最高酋长(祖先)
-
如果酋长相同(祖先相同),则说明属于同一部落,没事了,兄弟一场。
-
并: 如果酋长不相同(祖先不相同),则说明属于不同部落(来自不同的连通分量),需要打一架来大一统了,谁打输了,输方整个部落(连通分量)都要归顺过去。也就是输方的酋长(祖先),变成胜方酋长(祖先)的下属(孩子)。地球上的独立部落数目-1。(因为两个部落统一成一个了。)
-
最后这个地球上,很可能就实现了大一统 – 只有一个部落。
补充1 – 初始化:
- 初始化:地球上,很久很久以前,当所有的节点都没相遇的时候,各自为王,每个结点就是一个部落,部落只有他一个人,所以每个结点是自己的酋长。
- 然后两个结点偶然相遇,来到上面的第一步。
补充2 – 打架怎么定胜负 (规则很多,举两种来说):
- 很明显,按一种打架规则来分析,如果人多的部落输给人少的部落,这也是很难的,所以可以根据部落的人头数来决定。 (根节点的所有孩子的个数 size)
- 当然,如果按另一种打架规则来分析,如果一个部落治理的井井有条,从酋长到原始人之间,有很多的官职,层层管制,说明这个部落制度很完善,一定程度上说明他很先进噢,所以大可能也是他赢。 (根节点到叶节点的层数 - 深度)
具体为啥呢,大家想深入的可以看这篇文章。并查集算法笔记
本文点到为止,讲个浅显道理就可以啦~
题外话: 突然觉得,并查集难道是秦始皇发明的? 特爱一统六合。。。。。。
1579 保证图可完全遍历 – 由克鲁斯卡尔引入并查集
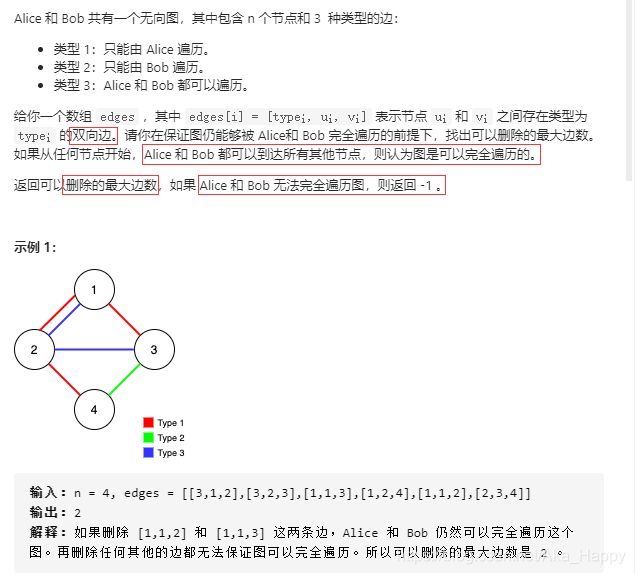
题目描述:
题目解读:
(题目解读部分摘自leetcode官方解答)
-
首先我们需要思考什么样的图是可以被 Alice 和 Bob 完全遍历的?
对于 Alice 而言,她可以经过的边是「Alice 独占边」以及「公共边」,由于她需要能够从任意节点到达任意 节点,那么就说明:
- Alice的目的是: 当图中仅有「Alice 独占边」以及「公共边」时,整个图需要是连通的,即整个图只包含一个连通分量。
- 对于 Bob 而言,当图中仅有「Bob 独占边」以及「公共边」时,整个图也需要是连通的才达成目的。
-
那么我们应该按照什么策略来添加边呢?
直觉告诉我们,「公共边」的重要性大于「Alice 独占边」以及「Bob 独占边」
因为「公共边」是 Alice 和 Bob 都可以使用的,而他们各自的独占边却不能给对方使用。
「公共边」的重要性也是可以证明的:

因此,我们可以遵从 优先添加「公共边」的策略。回顾本题,本题希望,用最少的边,能使 alice 和 bob 分别能成功遍历整个图, – 即可以删除最多的不必要边!
具体地,我们遍历每一条「公共边」,对于其连接的的两个节点:
如果这两个节点在同一个连通分量中,那么添加这条「公共边」是无意义的;
如果这两个节点不在同一个连通分量中,我们就可以(并且一定)添加这条「公共边」,然后合并这两个节点所在的连通分量。
这就提示了我们使用并查集来维护整个图的连通性,上述的策略只需要用到并查集的「查询」和「合并」这两个最基础的操作。
在处理完了所有的「公共边」之后,我们需要处理他们各自的独占边,而方法也与添加「公共边」类似。我们将当前的并查集复制一份,一份交给 Alice,一份交给 Bob。
- a. 为公共边建立一颗最小生成树,遵循 不成环的原则; 但不要求必须连通每个节点,
即 不强制: 边数=点数-1, 得到选中的公共边集 common_edge- b. 基于公共生成树,加入 alice 的独占边 作为备选集合,生成 alice 的并查集,得到Alice独特的parentDict,以及alice地图上的连通分量个数。
- c. 基于公共生成树,加入 bob 的独占边 作为备选集合,生成 bob 的并查集,得到bob独特的parentDict,以及bob地图上的连通分量个数。
如果alice 与 bob 能完全遍历,(这两个并查集都只包含一个连通分量),则计算可以删除的最大边数 |del_edge|。
- |total_edge| = |common_edge| + |alice_edge| + |bob_edge|
- |del_edge| = |all_edges| - |total_edge|
细节
在使用并查集进行合并的过程中,我们每遇到一次失败的合并操作(即需要合并的两个点属于同一个连通分量),
那么就说明当前这条边可以被删除,将答案增加 1。
代码分块讲解 (PK规则按每个酋长的孩子数 – 人多力量大)
初始化 Alice, bob 各自的连通分量计数器,初始化为节点个数N。
即初始化认为,多少个结点,就多少个连通分量。
import copy
class Solution:
def maxNumEdgesToRemove(self, n, edges):
self.bobSetCount = n # n个独立点
self.aliceSetCount = n # n个独立点
把全部边,按类型划分为,公共边集合,只有alice能走的边的集合,只有bob能走的边的集合。
# get common list, special list
common_edge_list, alice_edge_list, bob_edge_list = self.getSelfEdge(edges)
def getSelfEdge(self, edgesList):
common_edge_list, alice_edge_list, bob_edge_list = [], [], []
for edge in edgesList:
if edge[0] == 1:
alice_edge_list.append(edge)
elif edge[0] == 2:
bob_edge_list.append(edge)
elif edge[0] == 3:
common_edge_list.append(edge)
return common_edge_list, alice_edge_list, bob_edge_list
commonsize : 在公共生成树里,每个结点,麾下有多少个他的子民。 所有人初始化都为1,即麾下只有他自己咯。
先用并查集 self.unionAndSearch() 计算只有公共边的图,尽量保留足够多的公共必须边。
返回: 1. 公共边计算以后删除的边, 2. 公共边计算以后的parentDict, 3. 公共边生成生成树后整个图的连通子量个数
commonsize=[1]*(n+1)
# union & search set
common_delEdge, common_parentDict, common_SetCount = self.unionAndSearch(common_edge_list, n, commonsize)
commonsize : 在计算完公共生成树里,每个结点,麾下有多少个他的子民。
Alice, bob 都需要基于这个common_size,去生成自己的图。
# 初始化两个人的size,基于commond的基础上
alicesize = copy.deepcopy(commonsize); bobsize = copy.deepcopy(commonsize)
用并查集 self.unionAndSearch() 计算只有alice边的图,还有只有bob边的图
alice_delEdge, alice_parentDict, alice_SetCount = self.unionAndSearch(alice_edge_list, n, alicesize, common_parentDict, common_SetCount)
bob_delEdge, bob_parentDict, bob_SetCount = self.unionAndSearch(bob_edge_list, n, bobsize, common_parentDict, common_SetCount)
如果alice可以遍历整个图 (alice图的连通字量个数 alice_SetCount 为1 ),
同时 如果bob可以遍历整个图 (bob图的连通字量个数 bob_SetCount 为1 ),
就可以计算能删除多少条边,
if alice_SetCount == 1 and bob_SetCount == 1:
return (common_delEdge + alice_delEdge + bob_delEdge)
else:
return -1
附上并查集函数
def unionAndSearch(self, edgeList, n, childsize, parentDict=None, SetCount=None):
if parentDict is None:
parentDict = [-1]
for _ in range(1, n + 1, 1):
parentDict.append(_)
else:
parentDict = copy.deepcopy(parentDict)
if SetCount is None:
SetCount = n
delEdge = 0
for edge in edgeList:
start = edge[1]
end = edge[2]
start_par = self.findParent(start, parentDict)
end_par = self.findParent(end, parentDict)
if start_par != end_par:
if childsize[start_par] < childsize[end_par]:
start_par, end_par = end_par, start_par
'''驯服对方的时候,到底谁服从谁比较好!!! 非常重要,减少搜寻时间'''
parentDict[end_par] = start_par
# childsize[start_par]+=1
childsize[start_par]+=childsize[end_par] # 按麾下人头个数比较
SetCount -=1
else:
# 形成环路, 不予考虑
delEdge += 1
pass
return delEdge, parentDict, SetCount
def findParent(self, node, parentDict):
parent = parentDict[node]
while parent != node:
node = parent
parent = parentDict[node]
return parent
整体代码:
import copy
class Solution:
def maxNumEdgesToRemove(self, n, edges):
self.bobSetCount = n # n个独立点
self.aliceSetCount = n # n个独立点
commonsize=[1]*(n+1)
# get common list, special list
common_edge_list, alice_edge_list, bob_edge_list = self.getSelfEdge(edges)
# union & search set
common_delEdge, common_parentDict, common_SetCount = self.unionAndSearch(common_edge_list, n, commonsize)
# 初始化两个人的size,基于commond的基础上
alicesize = copy.deepcopy(commonsize); bobsize = copy.deepcopy(commonsize)
alice_delEdge, alice_parentDict, alice_SetCount = self.unionAndSearch(alice_edge_list, n, alicesize, common_parentDict, common_SetCount)
bob_delEdge, bob_parentDict, bob_SetCount = self.unionAndSearch(bob_edge_list, n, bobsize, common_parentDict, common_SetCount)
if alice_SetCount == 1 and bob_SetCount == 1:
return (common_delEdge + alice_delEdge + bob_delEdge)
else:
return -1
def getSelfEdge(self, edgesList):
common_edge_list, alice_edge_list, bob_edge_list = [], [], []
for edge in edgesList:
if edge[0] == 1:
alice_edge_list.append(edge)
elif edge[0] == 2:
bob_edge_list.append(edge)
elif edge[0] == 3:
common_edge_list.append(edge)
return common_edge_list, alice_edge_list, bob_edge_list
def unionAndSearch(self, edgeList, n, childsize, parentDict=None, SetCount=None):
if parentDict is None:
parentDict = [-1]
for _ in range(1, n + 1, 1):
parentDict.append(_)
else:
parentDict = copy.deepcopy(parentDict)
if SetCount is None:
SetCount = n
delEdge = 0
for edge in edgeList:
start = edge[1]
end = edge[2]
start_par = self.findParent(start, parentDict)
end_par = self.findParent(end, parentDict)
if start_par != end_par:
if childsize[start_par] < childsize[end_par]:
start_par, end_par = end_par, start_par
'''驯服对方的时候,到底谁服从谁比较好!!! 非常重要,减少搜寻时间'''
parentDict[end_par] = start_par
# childsize[start_par]+=1
childsize[start_par]+=childsize[end_par] # 按麾下人头个数比较
SetCount -=1
else:
# 形成环路, 不予考虑
delEdge += 1
pass
return delEdge, parentDict, SetCount
def findParent(self, node, parentDict):
parent = parentDict[node]
while parent != node:
node = parent
parent = parentDict[node]
return parent
终于初步写完了! 太累了!写了一下午。。。。不知道讲清楚了没。。。如果没讲清楚的地方可以留言,我再补充。
并查集的另外两题。。。过几天再写吧,累了累了,溜了溜了。。。。 2021/1/28