吴恩达机器学习（推荐系统）

（1）问题规划

这一章中将讨论推荐系统的有关内容，它是在机器学习中的一个重要应用。

机器学习领域的一个伟大思想：对于某些问题，有一些算法可以自动地学习一系列合适的特征，比起手动设计或编写特征更有效率。这是目前做的比较多的研究，有一些环境能让你开发某个算法来学习使用那些特征。

接下里让我们通过推荐系统的学习来领略一些特征学习的思想。

推荐系统预测电影评分的问题：

某些公司让用户对不同的电影进行评价，用0到5星来评级，下面是用户的评价情况：

符号介绍：

推荐系统就是在给出了r(i,j)和y(i,j)的值后，会去查找那些没有被评级的电影，并试图预测这些电影的评价星级。例如，在上述图中给出的结果，从Alice和Bob的评价中，他们给爱情片的评价比较高，可能预测他们没看过的电影也是4到5星；而Carol和Dave的评价中，对爱情片的评价低，而动作片的评价不错，所以他们对没看过的爱情片的评价会是0，而对动作片的评价可能会是4到5星。

因此，如果想开发一个推荐系统，那么需要想出一个学习算法—能自动填补这些缺失值的算法。这样就可以看到该用户还有哪些电影没看过，并推荐新的电影给该用户，可以去预测什么是用户感兴趣的内容。

这就是推荐系统问题的主要形式，接下来将讨论一个学习算法来解决这个问题。

（2）基于内容的推荐算法

这一节中将介绍一种建立推荐系统的方法：基于内容的推荐算法。

例如上一节中提到的预测电影的例子，如何预测未评价的电影呢？假设对于每一部电影，都有一个对应的特征集，如下图所示：

现在为了做出预测，可以把每个用户的评价预测值看作是一个线性回归问题，特别规定，对于每一个用户j，要学习参数向量θ^(j)，通常来说， θ(j)是一个n+1维，其中n是特征的数量。然后要预测用户j评价电影i的值，也就是参数向量θ(j)与特征向量x(j)的内积。

假如想预测用户1-Alice对电影3的评价，那么电影3会有一个参数向量，假如用某种方法得到了Alice的参数向量，那么Alice对电影3的预测就等于，如下图的计算：

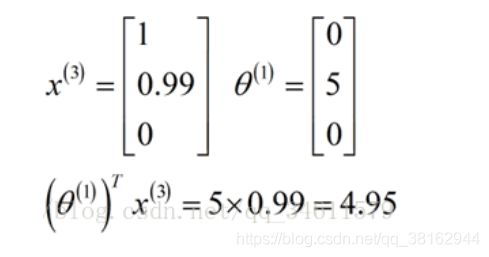
所以，上面的操作就是对每一个用户应用了一个不同的线性回归的副本，上述给出了Alice的线性方程。同样的，其他用户都有一个不同的线性方程，这就是预测评价的方法。

接下来给出问题的正式定义：

如果用户j给出了电影i的评价，就将r(i,j)记为1，而y(i,j)是对电影的评价的具体评价值；θ(j)是每个用户x(i)的一个参数，而x(i)是特定电影的一个特征向量，对于每个用户和电影，会给出预测x(i)。

用m(j)表示用户j评价电影的数量，那么为了学习参数向量θ(j)要怎么做呢？

这就像是线性回归，最小化参数向量θ(j)，加上正则化项，如下所示：
通过这个方法可以得到对参数向量θ(j)的估计值，当然，当构建推荐系统时，不仅要学习单个用户的参数，要学习所有用户的参数，可以得到公式：

为了实现最小化，推导梯度下降的更新公式如下：

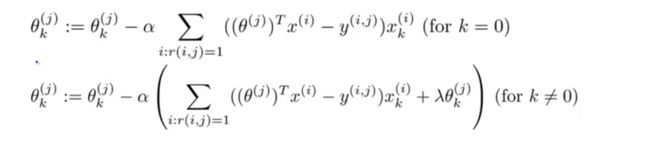
这就是如何将变量应用到线性回归中来预测不同用户对不同电影的评级，这里描述电影内容的特征量来做预测，这个特殊的算法叫做基于内容的推荐算法，接下来将介绍另一种推荐算法。

（3）协同过滤

这一节中将讨论用来构建推荐系统的方法，叫做协同过滤，这种算法能够自行学习要使用的特征。

这里还是用上一节中的预测电影的例子，但是不知道特征量具体的值，如下图所示：

假设这里采访了上述4个用户，他们告知了喜欢爱情电影的程度以及喜欢动作电影的程度，于是每个用户有了对应的θ(1)，θ(2)，θ(3)，θ(4).

如果能从用户得到例如上述的参数值，那么理论上就能推测出每部电影的x(1)和x(2)的值。

我们将这一学习问题标准化到任意特征x(i)，假设用户提供了θ(i)…θ(j)的值，而我们想要学习电影i的特征向量x(i)，要做的是优化目标函数：

当然，我们不仅要学习单个电影的特征，还要学习所有电影的所有特征，可以得到公式：

总结一下协同过滤的方法：

如果已知电影的特征量，可以根据不同电影的特征，学习参数θ，已知这些特征，就能学习出不同用户的参数θ；如果用户愿意提供这些参数θ，那么就能估计出各种电影的特征值。

那么通过θ–x--θ—x---θ—x这样的迭代过程，会得到更好的θ和x，如果重复这个过程，算法将会收敛到一组合理的电影特征以及一组合理的对不同用户的参数估计，这就是协同过滤。

这一节中，探讨了最基本的协同过滤算法，它指的是当你执行算法时，要观察大量的用户的实际行为来协同地得到更佳的每个人对电影的评分值，协同的另一层含义就是每个用户都在帮助算法更好地进行特征学习。

（4）协同过滤算法

这一节中将会结合前两节中讲述到的概念来设计协同过滤算法。

我们并不需要不停地重复计算，解出θ解出x再解出θ再解出x，实际上存在更有效率的算法可以将θ和同时计算出来，定义新的优化目标函数J，如下图所示：

这个代价函数将关于θ和x的两个代价函数合并起来，为了提出一个综合的优化目标问题，要做的是将这个代价函数视为特征x和用户参数θ的函数，对它的整体最小化：

所以，将上述所讲的结合起来，就得到了协同过滤算法：

▷ 首先会把θ和x初始化为小的随机值；

▷ 接下来用梯度下降或其他高级优化算法把代价函数J（x,x,x,θ,θ,θ）最小化；

▷ 最后，如果用户具有一些参数θ，电影带有已知的特征x，就可以预测出该用户给这部电影的评分会是:(θ^T)*X。

这就是协同过滤算法，可以使用它同时计算出θ和x。

（5）矢量化：低秩矩阵分解

这一节中将介绍协同过滤算法的向量化实现。

给定了数据如下：

将图中的数据写入矩阵中，会得到一个5行4列的矩阵：

矩阵中的Y(i,j)就是第j个用户给第i部电影的评分，用户j给第i部电影的评分的预测由公式(θ^T)*x给出，因此，预测评分的矩阵如下所示：

给定矩阵X和矩阵Θ的定义如下：

就可以用向量化的方法计算预测矩阵：XΘ^T，这个协同过滤算法有另一个名字叫做低秩矩阵分解。

接下来再介绍一个问题：利用已学到的属性来找到相关的电影。

假如有电影i，想要找到另一部与电影i相关的电影j，换个角度来说，如果用户正在看电影j，看完后推荐哪一部电影比较合理？

比如电影i有一个特征向量x(i)，如果找到另一个电影j特征向量x(j)，x(i)和x(j)的距离很小，||x(i)-x(j)||即很小，那么就很明显表明电影j和i相似，从这个意义上来说，喜欢看电影j的人也很可能喜欢看电影i。

因此，希望通过本节的学习，能够知道如何用一个向量化的实现来计算所有用户对所有电影的评分预测值，也可以实现利用已学到的特征，找到彼此相类似的电影。

（6）实施细节：均值规范化

这一节中将介绍在实现推荐算法过程中的细节：均值归一化。

考虑这样的例子，有一个用户没有给任何电影评分，如下图所示：

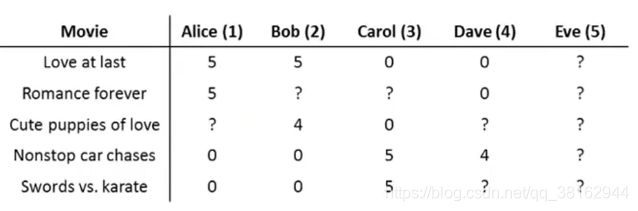
现在再来看一看协同过滤算法会对这个用户做什么，假设要学习两个特征变量，学习出参数向量θ^5的值会等于0，然后预测出Eve给电影的评分，用到的是公式，但是这样预测的结果都为0，显然不是我们想要的结果，接下来将用均值归一化的思想来解决这个问题。

将图中的数据写入矩阵中，得到一个5行5列的矩阵：

现在要实现均值归一化，要做是计算每个电影所得评分的均值：

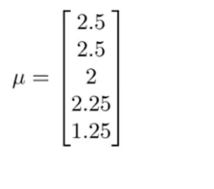
观察这些均值，现在用矩阵Y的每一列减去μ得到矩阵：

现在如果使用协同过滤算法进行预测，则假设这就是从用户那得到的实际评分，把它当做数据集，用来学习参数θ(j)和特征x(i)，即用这些均值归一化后的电影评分来学习。当想要进行预测时，步骤如下：

▷ 对用户j对电影i的评分预测它为：；（θ(j)和x(i)都是从均值归一化后数据集中学习出的参数，做预测的时候需要把减去的均值加回来）

▷ 对用户5：Eve来说，由于之前没有给电影进行评分，学习到的参数仍然会等于0，所以预测的评分为：
，所以即使前一项为0，预测的结果还是为u，这样的结果是有意义的。

所以，这就是均值归一化的实现，它作为协同过滤算法的预处理步骤，根据不同的数据集，有时能让算法表现的更好。