密码学 (cryptography I - Dan Boneh)【二】Stream ciphers
学习课程：斯坦福大学密码学公开课
课件链接：https://pan.baidu.com/s/1vogTE2Flpzi9DmoclLPGQw
提取码：1mrp
Stream ciphers
- The One Time Pad
- 学到此处的一些思考：熵与密码
- Pseudorandom Generators
- Negligible vs. non-negligible
- Attacks on OTP and stream ciphers
- Real-world Stream Ciphers
- PRG Security Defs
- Semantic security
- Stream ciphers are semantically secure
- 知识梳理
-
- 统计测试的作用是随机性检测
- 不可预测的PRG就是安全的PRG
- 语义安全性检测模型也是一个统计测试
- 统计测试中的优势和语义安全性中的优势
The One Time Pad
如何定义cipher。
cipher由通常由五元组构成：密钥空间K、明文空间M、密文空间C、加密算法E、解密算法D。
加密算法E通常是随机算法，它会自己生成随机序列，加入到密文的生成中；而解密算法D往往是确定算法，没有随机数的加入。
The One Time Pad：一次性密码本
明文密文空间都是长度为n的二进制序列。密钥空间也是。密钥是和明文等长的随机的二进制序列。
加密解密都是逐位异或。
简单的课堂小问题。
一次性密码本并不能在真实场景中运用。因为Alice必须把密钥K也安全地传给Bob。但如果Alice有这种方法，她完全可以安全地直接把消息传送过去。初次之外，因为密钥k必须和明文等长，因此在传输过程中存在着严重的数据冗余（k就是那个冗余信息，因为原来的目的只是把明文信息传输过去），使信息传输效率下降。
为什么一次性密码本是安全的呢。或者说什么是安全的密码，什么使密码安全。看下文。
攻击者只能发动唯密文攻击。
我们想通过加密方案，使攻击者不能还原密钥或者明文。
如果是完美的加密方案，那么会使攻击者不能获得任何与明文相关的信息。
Shannon关于完美加密方案的解释：任意两个等长的不同明文m0和m1经过加密后，结果为密文c的概率是一样的。这样的话，如果攻击者截获了一段密文，他就无法获取任何一点明文信息。因为不同明文经过加密变成密文c的概率是一样的。
这就很容易解释为什么一次一密是完美的加密方案，因为密钥是随机的，根据异或的性质，密文也是随机的，因此从密文中无法获取任何有关明文的信息。
因此唯密文攻击对一次一密的加密方式是无效的。
简单的课堂小问题。
要实现完美的安全性，密钥的长度必须不小于明文的长度。这在实际运用中很难实现。
学到此处的一些思考：熵与密码
在前面的学习中会发现，“随机”这个词经常出现。什么是随机？在数学中，通常用熵来衡量事物的随机性。
香农提出，完美的加密方案就是从密文中不能获取任何有关明文的知识。这是从密文到明文的一种阐述。换个角度，完美的加密方案就是一个明文有相同的概率变成任意一种密文。在明文变成密文的过程中，不确定性增加了，也就是熵增加了。
由此可见：好的加密方案就是通过加密尽可能地把明文的熵增大。
那么加密的过程中明文的熵为什么会增大呢？对于一个函数来说，输出的熵是不肯能大于输入的熵的。这时我们就会意识到，随机数和异或在加密过程中的重要性。
随机数的引入使函数的输入熵增大，而异或可以把随机数的熵传递给明文，这样函数的输出熵，也就是密文的熵就会增大。
由此可见一个好的随机数生成算法，在加密过程中是十分关键的。事实上，要想通过算法生成真正的随机序列是不可能的。
Pseudorandom Generators
上一章节的回顾。
引入伪随机数生成器G。G可以把种子空间映射到比种子空间{0,1}s大得多的伪随机序列空间{0,1}n。
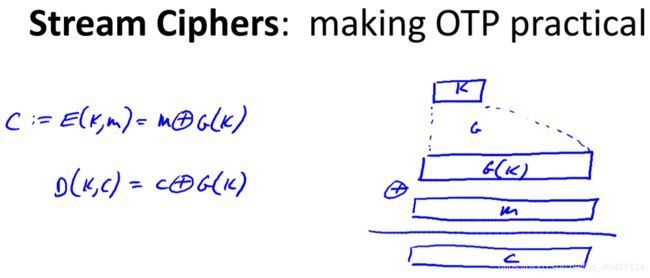
明文和G生成的伪随机序列进行异或。
简单的课堂小问题。
流密码是安全的，但不是香农定义的完美安全。我们需要一个新的关于安全的定义。流密码的安全性依赖于PRG。
PRG的生成必须是不可预测的。否则：网络一些协议往往有特定的前缀，攻击者可以通过这些前缀和其对应的密文，来算出PRG生成序列的前几位，进而预测整个序列。
给任意前缀都不能预测下一位。ε是可忽略值，表示可以接受的范围。如果预测正确的概率超过1/2+ε，那么就认为这个PRG不能用。
简单的课堂小问题。
几个弱PRG，容易被预测。以及，永远不要用glibc库里的随机函数做加密。
Negligible vs. non-negligible
用数学语言简单地解释了一下。
Attacks on OTP and stream ciphers
上节的回顾。
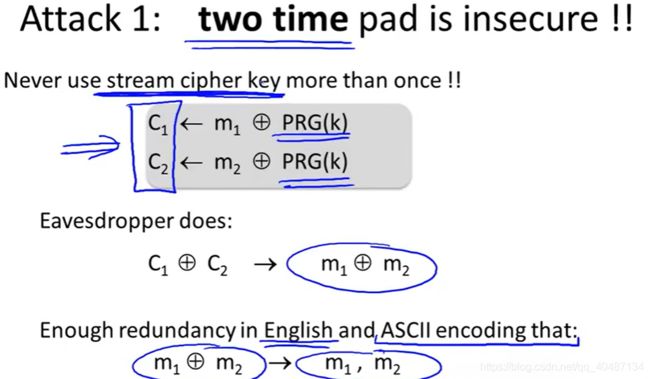
一次一密的安全性在于每次加密都用不同的密钥。如果一个密码本加密了两次不同的明文，就很容易导致信息的泄露。
例如：英文文本一般是用ASCII码编排的，而且英文本身就有规律可循。因此两个明文异或后的结果，还是有很大可能被解密。
几个例子（根据名字自行百度吧）：
Windows NT告诉我们，不同方向发送的信息流，需要不同的密码本。
WEP是个很糟糕的协议。图中，k是固定不变的，IV会在每个帧发送后+1。但IV是24位的，不能无限增长，在发送了大量帧后，又会归零。这相当于密码本复用了。而且每次重启设备后，IV都是从0开始的，这个也很不好。
WEP所使用的key是经过简单拼接而生成的，因此每个key都十分接近，这也很不安全。
一个更好的方案是用PPG为每一帧都生成一个key。
当用一次性密码本加密硬盘文件时，如果更改了明文某个地方，那么对应地方的密文也被更改了。攻击者就能通过密文更改的位置判断出明文更改的位置。但我们不想把这个信息泄漏给攻击者。一个好的加密方案应该是这样的：明文只要稍微改动一点，密文就有很大的变化，这样攻击者就无法从密文的改变推断出明文的哪个地方做了修改。
小结：永远不要重复使用流密钥。
网络中，每次会话应该协商新的密钥。
磁盘加密时，不要使用流密码方案加密。
流密码加密方案也不提供完整性支持，攻击者很容易篡改明文。
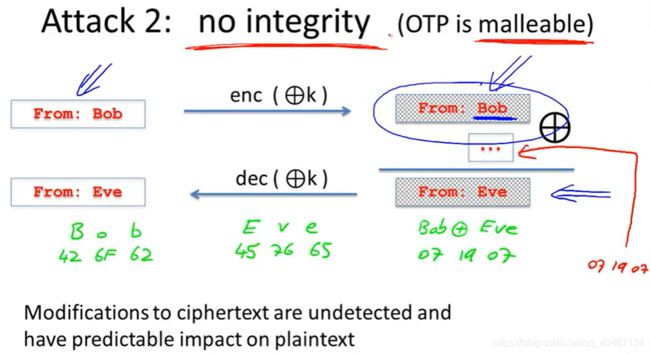
例如：加入攻击者知道一封邮件是由Bob寄来的，那么他可以通过修改密文的方式影响明文，把Bob修改为Eve。
Real-world Stream Ciphers
RC4生成的序列随机性不够。
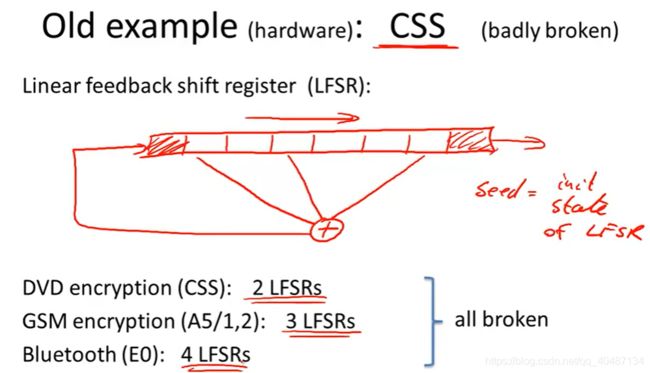
用于硬盘加密的CSS加密方案。它的key由线性反馈移位寄存器生成(LFSR)，其原理如下：
LFSR的初始态就是这个PRG的seed(密钥种子)。
CSS的原理：
首先CSS的seed是40位(美国法律规定)。这40位分别用在两个LFSR上。LFSR1是17位，LFSR2是25位。40=16+24。16位给LSFR1，并在这16位前添一个1构成17位，这17位就是LFSR1的初始态。LFSR2同理。LFSR1和LFSR2每次会运行8轮，产生的序列，会和上一次计算产生的进位三者相加，产生的值mod256，生成一个8位的序列，也就是一个字节的密钥。产生的8位序列和明文异或产生密文。
LFSR运行8轮和后面的mod256是呼应的。
CSS的破解：
DVD的加密使用了MPEG文件。如果知道明文的前缀，例如前二十个字节。这样就可以与密文的前二十个字节异或，得到PRG输出的前二十个字节。
如图：LFSR1生成的前几位序列记为直线1，LFSR2生成的前几位序列记为直线2。因为是选取的序列前几位，1+2等于1异或2。得到的序列记为直线3，在加密时，每次选取直线三的8位，即一个字节和明文异或来得到密文。
因此上文得到的PRG输出的前几位就是直线3。穷举LFSR1的初始状态，得到直线1的所有可能，就可以通过1异或3得到直线2的所有可能。20字节，可以用前50位计算出LFSR2的抽头序列，在用剩下的数据验证。验证成功后再用GVG中剩下的密文进行进一步验证。
如何计算抽头序列
引入了nonce。
eStream的一种，Salsa20。其关键在于h函数，但教程里没有细讲。
效率。
PRG Security Defs
PRG产生的序列是很有限的，是{0,1}n的子集。
如何判断PRG产生的序列随机性的好坏呢？
引入一个A函数来判断PRG产生序列随机性的好坏。A的定义有很多种。
如何评估A的好坏。定义了一个概念叫advantage如图，值越接近1性能越好。
简单的课堂小问题。
如何定义一个安全的PRG：对于任意的有效(efficient)统计测试A，A对于PRG的优势为0。efficient是一个十分重要的限定，因为有些A可能在多项式时间内无法求解。如果去掉这个限定的话是无法得出一个结论的。
我们无法证明一个PRG是安全的，因为我们无法穷举出所有A。
不可预测是安全的必要条件。
可以把之前关于不可预测性的知识，用在定义一个统计测试中。
姚证明了不可预测的PRG就是安全的PRG。
姚氏定理十分好用。例如上图的例子。用姚氏定理解释的话就是，因为这个PGR是不安全的(因为它的性质，很容易构造出一个统计测试来区分这个PRG产生的序列和随机序列)，所以肯定是可预测的。
引入一个符号来表示两个序列在计算上是不可区分的(computationally indistinguishable)。、
Semantic security
如何定义安全，在香农的定义上做了写改动。只要攻击者无法用现有的技术计算出有关明文的信息就行。
定义了语义安全性，在密码学中，这叫攻击者挑战者模型。
W0对应收到M0的密文，输出1;
W1对应收到M1的密文，输出1。
可以参考我下面这篇博客第三章 可证明安全性中的内容。
https://blog.csdn.net/qq_40487134/article/details/103875373
语义安全性的定义。
简单的小例子。
OPT是语义安全的。
Stream ciphers are semantically secure
Goal: secure PRG ⇒ semantically secure stream cipher
定理，用安全的PRG产生的流密钥进行流加密是语义安全的。
注意是语言安全，不是香农定义的完美安全。用PRG做流加密是不可能完美安全的。
想证明这个定理的话，可以证明它的逆否命题。
一个直观的证明。其中r是随机序列，G(k)是PRG产生的序列。如果PRG是安全的，那么攻击者无法区分，挑战者到底用的是r还是G(k)。
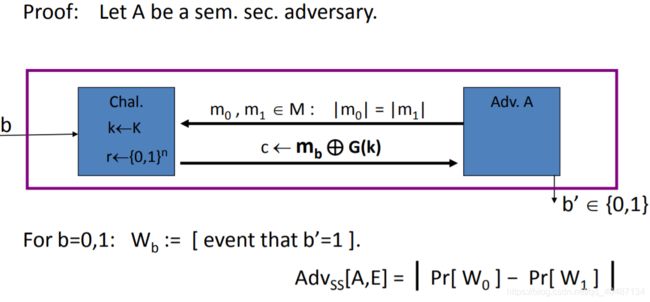
W0对应收到M0的密文，输出1;
W1对应收到M1的密文，输出1。
R0对应收到M0的密文，输出1;
R1对应收到M1的密文，输出1。
接下来要证明Claim2
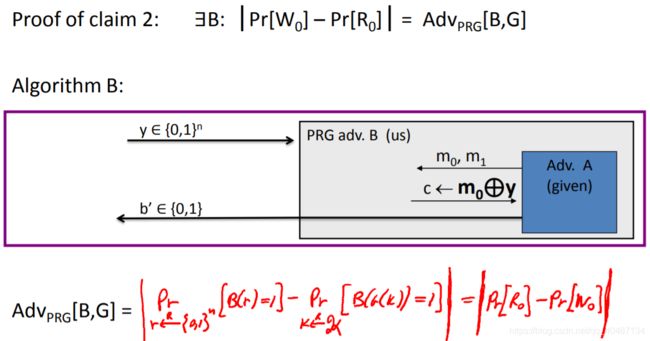
对这一套证明的理解在下面的知识梳理里。
知识梳理
统计测试的作用是随机性检测
统计测试是为了判断一个PRG是否能产生好的伪随机序列。若一个PRG产生的伪随机序列和真随机序列难以区分，那么就说这是一个安全的PRG。
不可预测的PRG就是安全的PRG
定义一个统计测试B，和一个有效的预测算法集合A，如果A预测到了结果，B就输出0，否则输出1。若B的优势接近于1，就说明序列随机性强。同样的，若B的优势接近于1，还说明A是不可预测的(因为预测到了结果回输出0)。
语义安全性检测模型也是一个统计测试
语义安全性检测模型是一个特殊的统计测试。在经典的统计测试中，输出的结果是我们自己定义的算法计算出来的。但在语义安全性检测模型中，统计测试的输出是就是攻击者的输出。
统计测试输出的含义是：这个PRG产生的序列随机性如何。
语义安全性检测中攻击者输出的含义是：攻击者对密文所对应的明文的判断，即判断challenger做了EXP(0)还是EXP(1)。
但二者并没有本质的区别，因为攻击者的优势还是与PRG产生序列的随机性有关。
归根到底，随机性越好，语义安全性越好，这也就是章节末的证明。
统计测试中的优势和语义安全性中的优势
虽然都是优势，但二者的区别还是很大的。
可以看到在PRG中左边输入是G(k)，右边输入是r。
但在SS中，W0和W1其实输入的都是G(k)。
这样说或许更明白，如果PRG中的优势是这样定义：
AdvPRG [A,G] = | Pr[ A(G(k))=0] - Pr[ A(G(k))=1] |
那么可以认为这两个情景中对优势的定义是等价的。
或许结合这个图会理解得更明白：
这也就是这个命题中2的由来
