【数据结构】基础二叉树、真二叉树、满二叉树、完全二叉树、二叉树的遍历
目录
- 树的介绍
- 树(Tree)的基本概念
- 二叉树(Binary Tree)
- 真二叉树(Proper Binary Tree)
- 满二叉树(Full Binary Tree)
- 完全二叉树(Complete Binary Tree)
- 二叉树的遍历
-
- 前序遍历(Preorder Traversal)
- 中序遍历(Inorder Traversal)
- 后序遍历(Postorder Traversal)
- 层序遍历(Postorder Traversal)
树的介绍
树(Tree)的基本概念
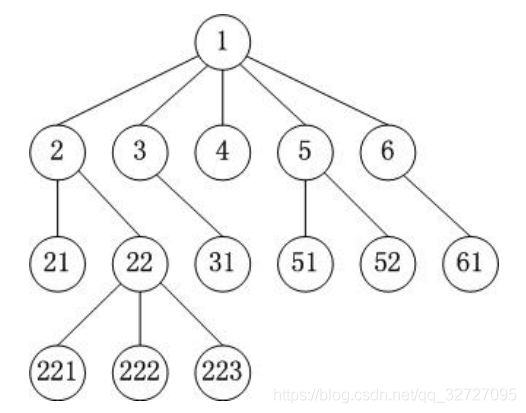
节点:上面的树形结构,是由若干个节点和节点之间,连接起来构成的结构,ABCDEFGH都是一个单独的节点。最上面的节点成为根节点。
根节点:根节点是树层次结构中的最高节点。换句话说,根节点是没有任何父节点的节点。
父节点和子节点:上面的B节点就是E和F节点的父节点,E和F节点就是B节点的子节点。
兄弟节点:拥有相同父节点的节点称为兄弟节点,例如 E和F节点拥有相同的父节点B,所以两者称为兄弟节点。反之 E和G节点没有相同的父节点,所有不是兄弟节点。
- 一棵树可以没有任何节点,称为空树
- 一棵树可以只有 1 个节点,也就是只有根节点
子树:以根节点的子节点作为根的节点称为子树。一个全树是由若干子树构成的。例如 树T1,T2和T3被称为根节点的子树。
节点的度(degree):子树的个数;指的是当前节点的子节点的个数,比如B节点的度为2,F节点的度为0,A节点的度为3。
树的度:所有节点中,最大的度,就是树的度。
叶子节点(leaf):没有任何子节点的节点,度为 0 的节点,只要树不是空树,就必然存在叶子节点。
非叶子节点:度不为 0 的节点。
路径:从一个节点到另一个节点经过的路径。比如上面把ABE连起来就是路径,至少两个节点才会构成路径。
层数(level):根节点在第 1 层,根节点的子节点在第 2 层,以此类推(有些也从第 0 层开始计算)
深度定义是从上往下的,高度定义是从下往上的。(其实不用在意这个,反正树的深度高度怎么数都一样的)。
深度和高度涉及到结点的层数,有的教材规定根结点在第0层,有的则规定根结点在第1层。原理都是一样的,因教材而异。
树从根结点开始往下数,叶子结点所在的最大层数称为 树的深度。
有的教材对于树的高度定义是高度就是深度(层数是0123,深度=高度=3;层数是1234,深度=高度=4);而有的教材树的高度则是看一共有几层。也就是说不论根节点在第几层,树的深度都是和最大层的叶子节点一样。而树的高度只要看有几层就行了(0123是四层,1234也是四层)。
节点的深度(depth):从根节点 到 当前节点的唯一路径上的节点总数,比如 E节点的深度为3,C节点的深度为2。
节点的高度(height):从当前节点 到 最远叶子节点的路径上的节点总数,比如 E节点的高度为1,B节点的深度为2。
树的深度:所有节点深度中的最大值;
树的高度:所有节点高度中的最大值;
数的深度 等于 树的高度
有序树:树中任意节点的子节点之间有顺序关系。
无序树:树中任意节点的子节点之间没有顺序关系,也称为 “自由树”。
森林:由 m(m ≥ 0)棵互不相交的树组成的集合。
二叉树(Binary Tree)
- 每个节点的度最大为 2(最多拥有 2 棵子树)
- 左子树和右子树是有顺序的,二叉树是有序树
- 即使某节点只有一棵子树,也要区分左右子树
-
非空二叉树的第
i层,最多有 2 i − 1 2^{i−1} 2i−1 个节点(i ≥ 1)举例:第一层 2 1 − 1 = 1 2^{1-1} = 1 21−1=1 个节点,第二层 2 2 − 1 = 2 2^{2-1} = 2 22−1=2 个节点,以此类推,第 i 层,最多有 2 i − 1 2^{i−1} 2i−1 个节点
-
在高度为
h的二叉树上最多有 2 h − 1 2^{h−1} 2h−1 个节点(h ≥ 1)举例:h = 3 ,第一层最多有1个,第二次最多有2个,第三次最多有4个,所以高为 3 的最有多 1 + 2 + 4 = 7 个节点,即 2 0 + 2 1 + 2 2 = 2 3 − 1 2^0+2^1+2^2=2^3-1 20+21+22=23−1 个节点
-
对于任何一棵非空二叉树,如果叶子节点个数为
n0,度为 2 的节点个数为n2,则有:n0 = n2 + 1假设度为 1 的节点个数为
n1,那么二叉树的节点总数n=n0 + n1 + n2
二叉树的边数:
度为1的节点有一个子树,所以就有一条边;度为2的节点有两个子树,所以就有两条边;度为0的节点没有子树,所以没有边,即T=n1 + 2 * n2。
从另一个角度看,每个节点的头部都有一条边,除了根节点以外,所以边数也 等于 总节点数 - 1,即T=n – 1=n0 + n1 + n2 – 1。
因此n1 + 2 * n2=n0 + n1 + n2 – 1,可得n0 = n2 + 1
真二叉树(Proper Binary Tree)
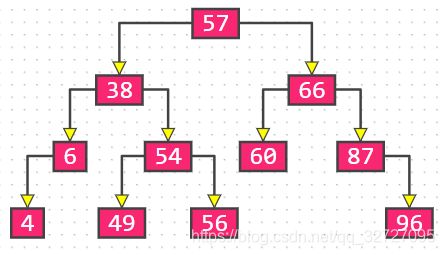
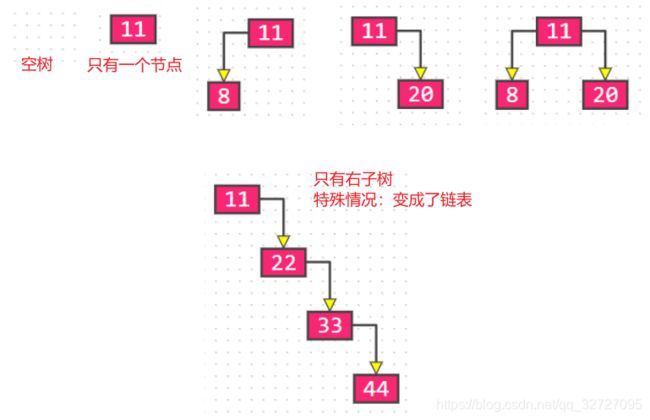
真二叉树:所有节点的度,要么为 0,要么为 2
注意:真二叉树不存在节点的度为1的情况
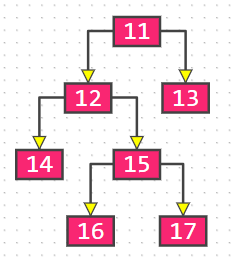
下图不是真二叉树,但是是二叉树:
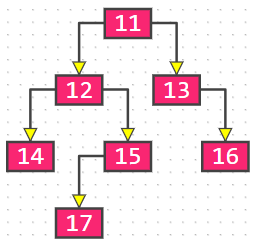
满二叉树(Full Binary Tree)
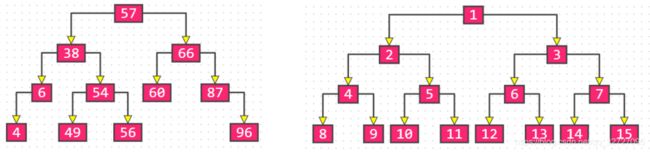
满二叉树:所有节点的度,要么为 0,要么为 2;且所以的叶子节点都在最后一层

假设满二叉树的高度为 h(h ≥ 1),那么 第 i 层的节点数量: 2 i − 1 2^{i − 1} 2i−1
叶子节点数量: 2 h − 1 2^{h − 1} 2h−1
总节点数量 n
n = 2 h 2^{h} 2h - 1 1 1 = 2 0 2^{0} 20 + 2 1 2^{1} 21 + 2 2 2^{2} 22 + ⋯ + 2 h − 1 2^{h − 1} 2h−1
h = l o g 2 ( n log_2(n log2(n + 1 ) 1) 1)
在同样高度的二叉树中,满二叉树的叶子节点数量最多、总节点数量最多。
满二叉树一定是真二叉树,真二叉树不一定是满二叉树
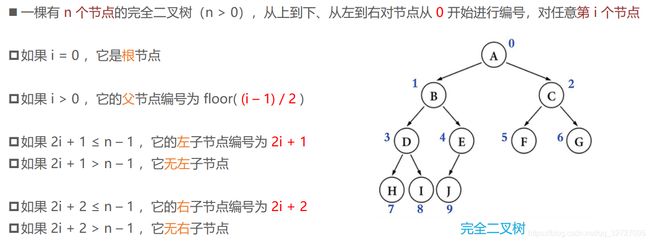
完全二叉树(Complete Binary Tree)
完全二叉树:对节点从上至下、左至右开始编号,其所有编号都能与相同高度的满二叉树中的编号对应;
叶子节点只会出现最后 2 层,最后 1 层的叶子结点都靠左对齐

◼ 完全二叉树从根结点至倒数第 2 层是一棵满二叉树
◼ 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
完全二叉树的性质
◼ 度为 1 的节点要么是 1 个,要么是 0 个
◼ 度为 1 的节点只有左子树
◼ 同样节点数量的二叉树,完全二叉树的高度最小
◼ 假设完全二叉树的高度为 h( h ≥ 1),那么
至少有 2 h − 1 2^{h − 1} 2h−1 个节点( 2 0 2^{0} 20 + 2 1 2^{1} 21 + 2 2 2^{2} 22 + ⋯ + 2 h − 2 2^{h − 2} 2h−2 + 1 1 1) 就是最后一层只有一个节点
最多有 2 h 2^{h} 2h - 1 1 1 个节点( 2 0 2^{0} 20 + 2 1 2^{1} 21 + 2 2 2^{2} 22 + ⋯ + 2 h − 1 2^{h − 1} 2h−1,满二叉树 )
总节点数量为 n
2 h − 1 ≤ n ≤ 2 h − 1 2^{h − 1} ≤ n ≤ 2^h-1 2h−1≤n≤2h−1 也可以表示为: 2 h − 1 ≤ n < 2 h 2^{h − 1} ≤ n < 2^h 2h−1≤n<2h
对两边取对数,可得 h − 1 ≤ l o g 2 n < h h − 1 ≤ log_2n < h h−1≤log2n<h
结论:就是比 l o g 2 n log_2n log2n 大的最小整数,即 h = f l o o r ( l o g 2 n ) + 1 h = floor( log_2n ) + 1 h=floor(log2n)+1
➢ floor(向下取整):只取前面的整数部分,例如 f l o o r ( 4.6 ) = 4 floor(4.6) = 4 floor(4.6)=4
➢ ceiling(向上取整):如果小数不为0,取前面的整数加1,否则只取前面的整数,例如 c e i l i n g ( 4.6 ) = 5 ceiling(4.6)=5 ceiling(4.6)=5, c e i l i n g ( 4.0 ) = 4 ceiling(4.0)=4 ceiling(4.0)=4
二叉树的遍历
遍历是数据结构中的常见操作:把所有元素都访问一遍;
线性数据结构的遍历比较简单:
- 正序遍历
- 逆序遍历
根据节点访问顺序的不同,二叉树的常见遍历方式有 4 种:
深度优先遍历(Depth First Search)
- 前序遍历(Preorder Traversal):树状结构展示(注意左右子树的顺序)
- 中序遍历(Inorder Traversal):二叉搜索树的中序遍历按升序或者降序处理节点
- 后序遍历(Postorder Traversal):适用于一些先子后父的操作
广度优先遍历(Breath First Search)
- 层序遍历(Level Order Traversal):计算二叉树的高度、判断一棵树是否为完全二叉树
前序遍历(Preorder Traversal)
访问顺序:根节点、前序遍历左子树、前序遍历右子树
下图前序遍历的结果是:7、4、2、1、3、5、9、8、11、10、12
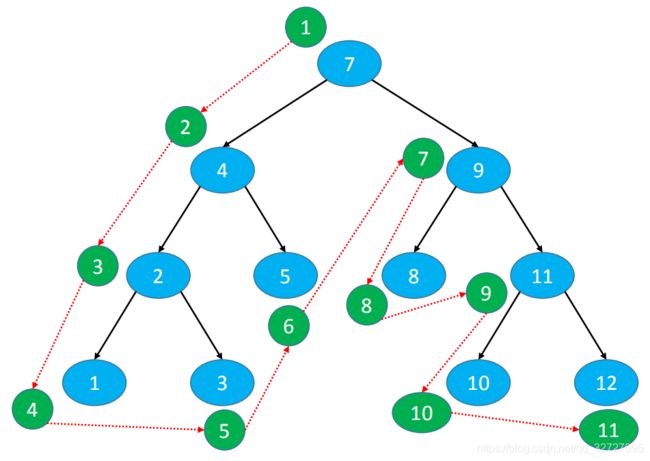
二叉树的前序遍历:https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>();
// 递归
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) return list;
list.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return list;
}
// 迭代一
/*
1. 设置 node = root
2. 循环执行以下操作(栈为空 或 node为空,结束遍历)
如果 node != null (一直访问左子节点,直到左子节点为空)
对 node 进行访问
将 node 入栈
设置 node = node.left
如果 node == null
弹出栈顶元素并赋值给 node
设置 node = node.right
*/
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) return list;
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
if (node != null) {
list.add(node.val);
stack.push(node);
node = node.left;
} else {
node = stack.pop();
node = node.right;
}
}
return list;
}
// 迭代二
/*
1. 将 root 入栈
2. 循环执行以下操作,直到栈为空
弹出栈顶节点 top,进行访问
将 top.right 入栈
将 top.left 入栈
*/
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) return list;
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root;
stack.push(node);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
list.add(node.val);
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
return list;
}
}
中序遍历(Inorder Traversal)
访问顺序:中序遍历左子树、根节点、中序遍历右子树
下图前序遍历的结果是:1、2、3、4、5、7、8、9、10、11、12
另一种中序遍历访问顺序:中序遍历右子树、根节点、中序遍历左子树
则下图的中序遍历的结果是:8、9、10、11、12、7、1、2、3、4、5、
二叉搜索树的中序遍历结果:是升序 或者 降序的

二叉树的中序遍历: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>();
// 递归
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null) return list;
inorderTraversal(root.left);
list.add(root.val);
inorderTraversal(root.right);
return list;
}
// 迭代
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null) return list;
Stack<TreeNode> stack = new Stack<>();
TreeNode node = root;
while (!stack.isEmpty() || node != null) {
//这是模拟递归的调用
if (node != null) {
// 如果当前节点不为null,就不断往左节点方向走,
stack.push(node); // 每走一次就将当前节点保存到栈中
node = node.left;
} else {
// 如果当前节点为null,说明左边走到头了,
node = stack.pop(); // 然后从栈中弹出节点,并赋给当前节点node
list.add(root.val);
node = node.right; // 然后转向当前节点的右边节点,继续上面整个过程
}
}
return list;
}
}
后序遍历(Postorder Traversal)
访问顺序:后序遍历左子树、后序遍历右子树、根节点
下图前序遍历的结果是:1、3、2、5、4、8、10、12、11、9、7

二叉树的后序遍历:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<Integer>();
// 递归
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null) return list;
postorderTraversal(root.left);
postorderTraversal(root.right);
list.add(root.val);
return list;
}
// 迭代
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null) return list;
Stack<TreeNode> s1 = new Stack<>();
Stack<TreeNode> s2 = new Stack<>();
TreeNode node = root;
s1.push(node);
while (!s1.isEmpty()) {
node = s1.pop();
s2.push(node);
if (node.left != null) {
s1.push(node.left);
}
if (node.right != null) {
s1.push(node.right);
}
}
while (!s2.isEmpty()) {
node = s2.pop();
list.add(root.val);
}
return list;
}
}
层序遍历(Postorder Traversal)
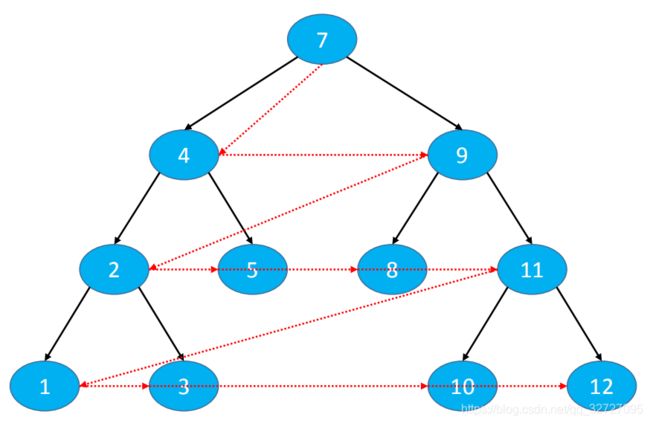
访问顺序:从上到下、从左到右依次访问每一个节点
下图前序遍历的结果是:7、4、9、2、5、8、11、1、3、10、12
二叉树的层次遍历: https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<List<Integer>> resList = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return resList;
Queue<TreeNode> queue = new LinkedList<>();
int levelSize = 1;
queue.offer(root);
List<Integer> list = new ArrayList<>(); ;
while(!queue.isEmpty()){
TreeNode node = queue.poll();
list.add(node.val);
levelSize--;
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
if(levelSize == 0){
resList.add(list);
levelSize = queue.size();
list = new ArrayList<>();
}
}
return resList;
}
}