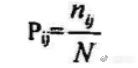【故障检测问题】基于免疫算法求解故障检测问题matlab源码
一、简介
1 故障检测问题
免疫算法的基础就在于如何计算抗原与抗体、抗体与抗体之间的相似度,因此免疫算法在处理相似性方面有着独特的优势。
基于人工免疫的故障检測和诊断模型如图所示。
在此模型中,用一个N维特征向量表示系统工作状态的数据。为了减少时间的复杂度,对系统工作状态的检测分为如下两个层次:
(1)异常检测:负责报告系统的异常工作状态。
(2)故障诊断:确定故障类型和发生的位置。
描述系统正常工作的自体为第一类抗原,用于产生原始抗体;描述系统工作异常的非自体作为第二类抗原,用于刺激抗体进行变异和克隆进化,使其成熟。
下面采用免疫算法对诊断知识的获取技术进行举例讲解。
基本思想是将想要求解的各类优化问题的目标函数(约束条件)与抗原相对应,找到可以与抗原进行亲和反应的抗体,该抗体就是要求的最优解。
最核心要解决的就是
1.计算抗原和抗体的亲和度,亲和度越高,越可能是最优解,
2.计算抗体和抗体间的相似度,调查抗体群具有的多样性。
IA是必须要产生多样性抗体和抗原去抗衡。具体的流程图如下:
计算方式:信息熵
利用信息理论,用抗体的信息量去描述抗体的多样性,以及抗体和抗原的亲和度
一个免疫系统有N个抗体构成,也就是一个抗体群
多样性用信息熵来表示
生成新的抗体群过程中要控制相同抗体的数量,这就需要在这一过程中计算抗体的相似度。
每个抗体会计算它与其他抗体间的相似性,然后计算该抗体的浓度。
首先我们需要识别抗原(也就是要知道要解决的问题是什么?)
IA是必须要产生多样性抗体和抗原去抗衡,从而找到最优解。
当我们识别抗原以后,我们会随机产生一个初始抗体群,对于抗体群的大小,和抗体长度都是我们自定义的参数值。
现在假设一个免疫系统的初始抗体群如下图所示:抗体群大小为N,遗传因子共M位
针对抗体群计算各个遗传因子的信息熵再计算整体的信息熵
为了判断抗体是否具有多样性,根据信息论的定义,我们用信息熵来表示抗体的多样性,抗体由m位遗传因子构成,先计算各个遗传因子的信息熵
Pij表示在j位置的遗传因子取值i的概率(遗产因子的取值范围是s个符号离散值)。
N个抗体对应共N个在j位置的遗传因子。那么这N个值中假设取值为i符号的有nij个,那么
再计算该抗体群的信息熵,共M位遗传因子组成一个完整的抗体qun
生成新的抗体群过程中要控制相同抗体的数量,这就需要在这一过程中计算抗体的相似度。
H(u,v)----由u,v两个抗体组成的新抗体群,计算对应的熵。(相当于计算新抗体群多样性)
抗原抗体亲和度计算
核心问题就是设定好所求问题的目标函数,一般目标函数会有很多未知参数,
找出能够完全亲和抗原的抗体,也就是找到了最优的解。
若没有找到,则需要ju,交叉具体异等方式去更新抗体库,生成新的抗体,同时将更新记忆细胞。
具体步骤如下:
(1)抗原识别,即理解待优化的问题,对问题进行可行性分析,提取先验知识,构造出合适的亲和度函数,并制定各种约束条件。
(2)初始抗体群,通过编码把问题的可行解表示成解空间中的抗体,在解的空间内随机产生一个初始种群。
(3)对种群中的每一个可行解进行亲和度评价。(记忆单元的更新:将与抗原亲和性高的抗体加入到记忆单元,并用新加入的抗体取代与其亲和性最高的原有抗体(抗体和抗体的亲和性计算))
(4)判断是否满足算法终止条件;如果满足条件则终止算法寻优过程,输出计算结果;否则继续寻优运算。
迭代:(5)(6)(7)
(5)计算抗体浓度和激励度。(促进和抑制抗体的产生:计算每个抗体的期望值,抑制期望值低于阈值的抗体;可以知道与抗原间具有的亲和力越高,该抗体的克隆数目越高,其变异率也越低)
(6)进行免疫处理,包括免疫选择、克隆、变异和克隆抑制。
免疫选择:根据种群中抗体的亲和度和浓度计算结果选择优质抗体,使其活化;
克隆:对活化的抗体进行克隆复制,得到若干副本;
变异:对克隆得到的副本进行变异操作,使其发生亲和度突变;
克隆抑制:对变异结果进行再选择,抑制亲和度低的抗体,保留亲和度高的变异结果。
(7)种群刷新,以随机生成的新抗体替代种群中激励度较低的抗体,形成新一代抗体,转步骤(3)。
二、源代码
clear all;
clc
global popsize length min max N code;
N=11; % 每个染色体段数(十进制编码位数)
M=110; % 进化代数
popsize=20; %设置初始参数,群体大小
length=10; % length为每段基因的二进制编码位数
chromlength=N*length; %字符串长度(个体长度),染色体的二进制编码长度
pc=0.7; %设置交叉概率,本例中交叉概率是定值,若想设置变化的交叉概率可用表达式表示,或从写一个交叉概率函数,例如用神经网络训练得到的值作为交叉概率
pm=0.3; %设置变异概率,同理也可设置为变化的
bound={-100*ones(popsize,1),zeros(popsize,1)};min=bound{1};max=bound{2};
pop=initpop(popsize,chromlength); %运行初始化函数,随机产生初始群体
ymax=500;
K=1;
P % 结果为(i*popsie)个监测器(抗体)
plot(1:M,favg)
title('个体适应度变化趋势')
xlabel('迭代数')
ylabel('个体的适应度')
function [bestindividual,bestfit]=best(pop,fitvalue)
global popsize N length;
bestindividual=pop(1,:);
bestfit=fitvalue(1);
Cmin=0;
for i=1:popsize
if objvalue(i)+Cmin>0 % objvalue 为一列向量
temp=Cmin+objvalue(i);
else
temp=0;
end
fitvalue(i)=temp; % 得一向量
end
end
function [newpop]=mutation(pop,pm)
global popsize N length;
for i=1:popsize
if(rand三、运行结果
具体运行结果图见完整代码
设置的故障数据属于三种故障类型的概率P值如下:
P=
0.800000000000 0.050000000000 1.000000000000
这表示故障数据属于故障一概率为80%,属于故障二的概率为5%,属于故障三的概率为100%。