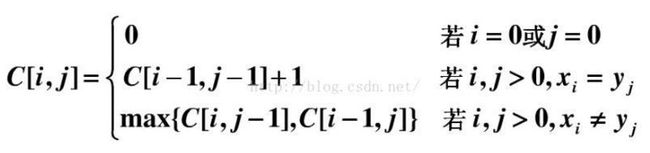最长公共子序列_动态规划——最长公共子序列

最近看了MIT算法导论课程里的动态规划部分，课程里用最长公共子序列问题来讲述动态规划，下去之后看了看代码，大概知道了怎么求解这个问题。

动态规划

动态规划算法通常用于求解具有某种最优性质的问题。我对动态规划的理解还比较浅显，目前认为动态有这几个特点：

1. 把原问题分解为子问题，这个有点像分治法，但与分治法不同的是，动态规划里上一级问题的求解依赖于下一级问题的解答，而在分治法里，如归并排序，即使下一子集没有排好序，上一级代码也可以得到执行（不过答案就不对了）。
2. 动态规划存在重复计算的子问题，一般为了避免重复计算而不会用递归。
3. 动态规划将未知转化成已知。

最长公共子序列

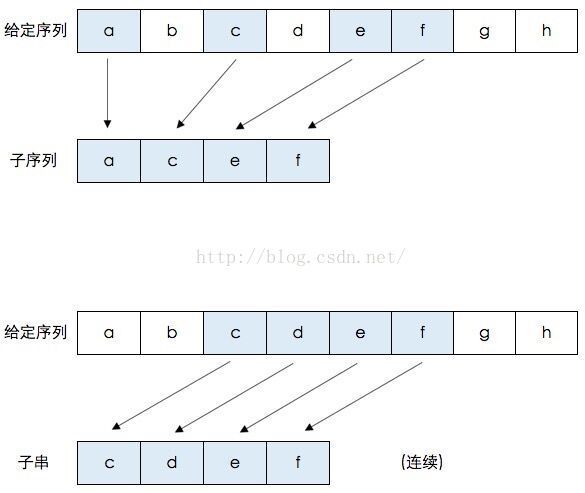
子序列： 一个序列A ＝ a1,a2,……an,中任意删除若干项，剩余的序列叫做A的一个子序列。也可以认为是从序列A按原顺序保留任意若干项得到的序列。

最长公共子序列（longest common sequence）和最长公共子串（longest common substring）不是一回事儿。

公共子序列 ： 顾名思义，如果序列C既是序列A的子序列，同时也是序列B的子序列，则称它为序列A和序列B的公共子序列。

最长公共子序列：A和B的公共子序列中长度最长的（包含元素最多的）叫做A和B的公共子序列。

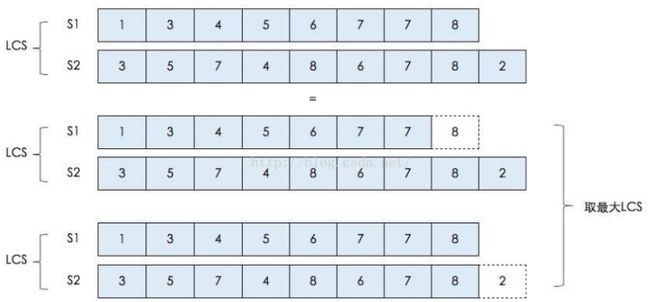
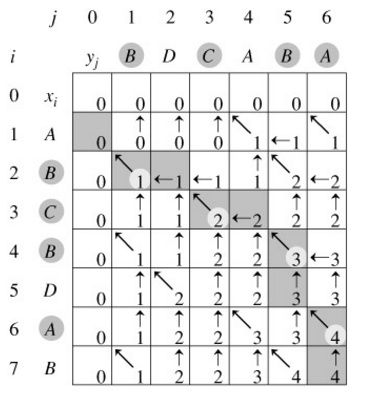
分析：

废话不多说，直接上公式：

代码：

def lcs(a, b):
    lena = len(a)
    lenb = len(b)
    c = [[0 for i in range(lenb + 1)] for j in range(lena + 1)]
    flag = [[0 for i in range(lenb + 1)] for j in range(lena + 1)]
    for i in range(lena):
        for j in range(lenb):
            if a[i] == b[j]:
                c[i + 1][j + 1] = c[i][j] + 1
                flag[i + 1][j + 1] = 'ok'
            elif c[i + 1][j] > c[i][j + 1]:
                c[i + 1][j + 1] = c[i + 1][j]
                flag[i + 1][j + 1] = 'left'
            else:
                c[i + 1][j + 1] = c[i][j + 1]
                flag[i + 1][j + 1] = 'up'
    return c, flag


def printLcs(flag, a, i, j):
    if i == 0 or j == 0:
        return
    if flag[i][j] == 'ok':
        printLcs(flag, a, i - 1, j - 1)
        print(a[i - 1], end='')
    elif flag[i][j] == 'left':
        printLcs(flag, a, i, j - 1)
    else:
        printLcs(flag, a, i - 1, j)


a='ABCBDAB'
b='BDCABA'
c,flag=lcs(a,b)
for i in c:
    print(i)
print('')
for j in flag:
    print(j)
print('')
printLcs(flag,a,len(a),len(b))
print('')

output:
[0, 1, 1, 1, 1, 2, 2]
[0, 1, 1, 2, 2, 2, 2]
[0, 1, 1, 2, 2, 3, 3]
[0, 1, 2, 2, 2, 3, 3]
[0, 1, 2, 2, 3, 3, 4]
[0, 1, 2, 2, 3, 4, 4]

[0, 0, 0, 0, 0, 0, 0]
[0, 'up', 'up', 'up', 'ok', 'left', 'ok']
[0, 'ok', 'left', 'left', 'up', 'ok', 'left']
[0, 'up', 'up', 'ok', 'left', 'up', 'up']
[0, 'ok', 'up', 'up', 'up', 'ok', 'left']
[0, 'up', 'ok', 'up', 'up', 'up', 'up']
[0, 'up', 'up', 'up', 'ok', 'up', 'ok']
[0, 'ok', 'up', 'up', 'up', 'ok', 'up']

BCBA

参考：

动态规划 最长公共子序列 过程图解​blog.csdn.net

动态规划基础篇之最长公共子序列问题 - CSDN博客​blog.csdn.net