Matlab中margin函数使用

目录

                                               margin函数

一.margin函数语法

1.输入参数

2.输出参数

二.说明

三.margin函数使用

1、传递函数的图增益和相位裕度

2.传递函数的增益和相位裕度

3、使用频率响应数据的增益和相位裕度

4、阵列中模型的增益和相位裕度

---

                                               margin函数

一.margin函数语法

• margin(sys)
• [Gm,Pm,Wcg,Wcp] = margin(sys)
• [Gm,Pm,Wcg,Wcp] = margin(mag,phase,w)
• [Gm,Pm] = margin(sys,J1,...,JN)

1.输入参数

sys—动态系统
动态系统模型| 模型数组

动态系统，指定为SISO动态系统模型或SISO动态系统模型的数组。

J1,...,JN—数组中要提取其正整数的增益和相位裕量的模型的索引

要提取其增益和相位裕量的数组中的模型的索引，指定为正整数。

mag—系统响应
3-D数组的大小

系统响应的幅度，以绝对单位表示，指定为3D数组。由于仅接受SISO系统，因此 是一个1×1×N数组，其中N是频点数。

phase—系统响应3-D阵列的相位

系统响应的相位（以度为单位），指定为3D数组。由于 仅接受SISO系统，因此 是一个1×1×N数组，其中N是频点数。

w—获得系统响应的幅度和相位值的频率
列矢量

获得系统响应的幅度和相位值的频率，指定为列向量。

2.输出参数

Gm—增益裕度
标量| 数组

增益裕度，以标量或数组形式返回。如果sys是：

• 然后，将单个模型Gm作为标量返回。

• 则模型阵列Gm是中每个模型的增益裕度阵列sys。

Gm是在Wcg相位角为–180°（模360°）的频率下使环路增益统一所需的增益变化量。换句话说，如果g是–180°相位频率的增益，则增益裕度为1 / g。负增益裕度表示通过降低增益而失去稳定性，而正增益裕度表示通过增加增益而失去稳定性

增益裕度Gm以绝对单位计算。可以通过以下公式计算以dB为单位的增益裕度：

Gm_dB = 20 * log10（Gm）

Pm—相位裕度
量标量| 数组

相位裕量，以标量或数组形式返回。如果sys是：

• 然后，将单个模型Pm作为标量返回。

• 一个模型数组，则Pm是中每个模型的相位裕度的数组sys。

相位裕度是环路增益为1.0时响应的相位与–180°之间的差。

Wcg—相位穿越频率
标量

相位穿越频率，以标量形式返回。Wcg是测量增益裕度的频率，它是相位为–180°时所对应的频率。Wcg以rad/TimeUnit为单位，其中TimeUnit 是的TimeUnit属性中指定的单位sys。

Wcp—增益穿越频率
标量

增益交叉频率，以标量形式返回。Wcp是测量相位裕量的频率，它是0dB增益所对应的频率。Wcp以radians/TimeUnit为单位，其中TimeUnit 是的TimeUnit属性中 指定的单位sys。

二.说明

margin（sys）：在屏幕上绘制sys的Bode响应，并在该图上指示增益和相位裕度。 增益裕度在图中以dB表示。

[Gm，Pm，Wcg，Wcp] = margin（sys）：返回以绝对单位表示的增益裕度Gm，相位裕度Pm以及sys的相应频率Wcg和Wcp。 Wcg是测量增益裕度的频率，它是–180°的相交频率。 Wcp是测量相位裕度的频率，它是一个0 dB的增益交叉频率。 这些频率以弧度/ TimeUnit表示，其中TimeUnit是sys的TimeUnit属性中指定的单位。 当sys有多个分频点时，裕度返回最小的增益和相位裕度以及相应的频率。

[Gm，Pm，Wcg，Wcp] = margin（mag，phase，w）：从频率响应数据中得出增益和相位裕量。 以绝对单位提供增益数据mag，以度为单位提供相位数据phase。 可以以任何单位提供频率向量w，并且余量以相同单位返回Wcg和Wcp。

[Gm，Pm] = margin（sys，J1，...，JN）：返回带有下标（J1，...，JN）的模型数组sys中条目的增益裕度Gm和相位裕度Pm。

三.margin函数使用

1、传递函数的图增益和相位裕度

创建一个连续传递函数：

sys = tf(1,[1 2 1 0])

sys =
 
         1
  ---------------
  s^3 + 2 s^2 + s

连续时间传递功能。以图形方式显示增益和相位裕量。

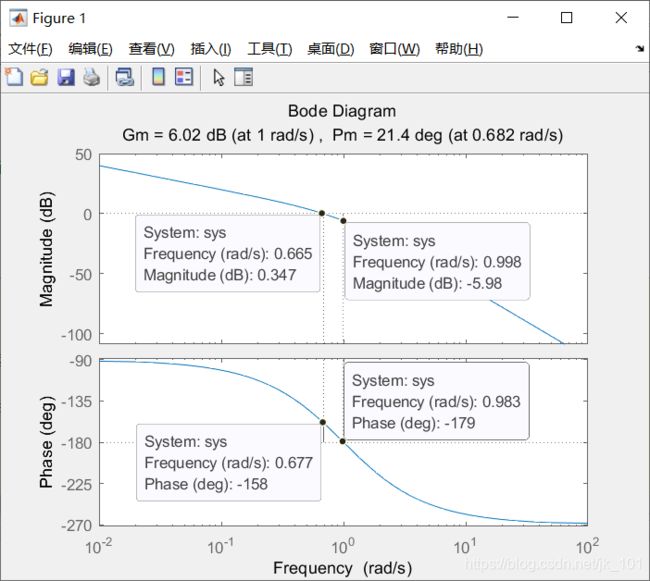
margin(sys)

如图所示：

                       

标题中显示的增益裕度（6.02 dB）和相位裕度（21.4度）用垂直实线标记。 垂直虚线表示Wcg（测量增益裕度的频率）和Wcp（测量相位裕度的频率）的位置。

2.传递函数的增益和相位裕度

创建一个离散时间传递函数：

sys = tf([0.04798 0.0464],[1 -1.81 0.9048],0.1)

sys =
 
   0.04798 z + 0.0464
  ---------------------
  z^2 - 1.81 z + 0.9048

采样时间：0.1秒
离散时间传递功能。

计算增益裕度，相位裕度和频率：

[Gm,Pm,Wcg,Wcp] = margin(sys)

Gm = 2.0517
Pm = 13.5711
Wcg = 5.4374
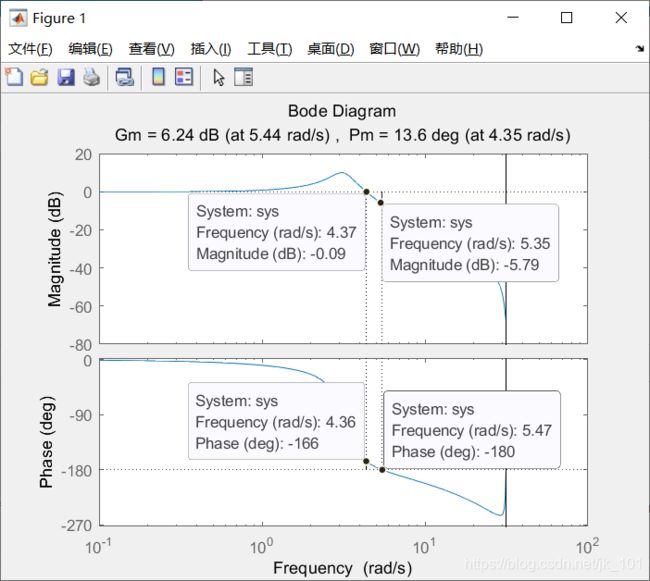
Wcp = 4.3544

如图所示：

                      

结果表明，在增益交叉频率为5.43 rad / s时，增益变化超过2.05 dB会导致系统不稳定。 同样，在4.35 rad / s的相交频率下，超过13.57度的相位变化将导致系统失去稳定性。

3、使用频率响应数据的增益和相位裕度

加载开环系统的频率响应数据，该数据包括在w的频率下测得的幅值（m）和相位值（p）：

load('openLoopFRD.mat','p','m','w');

计算增益和相位裕度：

[Gm,Pm,Wcg,Wcp] = margin(m,p,w)

Gm = 0.6249
Pm = 48.9853
Wcg = 1.2732
Wcp = 1.5197

如图所示：

                       

4、阵列中模型的增益和相位裕度

加载倒置的PendulumArray.mat，其中包含一个3×3的倒立摆模型阵列。 当您沿着sys的单个列在模型之间移动时，摆锤的质量会发生变化，而当您沿着单行移动时，摆锤的长度也会发生变化。 使用的质量值为100g，200g和300g，并且使用的摆长度分别为3m，2m和1m。

load('invertedPendulumArray.mat','sys');
size(sys)

                                                    

查找阵列中所有模型的增益和相位裕量：

[Gm,Pm] = margin(sys)

Gm = 3×3

    0.9800    0.9800    0.9800
    0.9800    0.9800    0.9800
    0.9800    0.9800    0.9800

Pm = 3×3

  -11.3565  -11.3898  -11.4228
  -11.3842  -11.4088  -11.4333
  -11.4020  -11.4208  -11.4396

margin返回两个数组Gm和Pm，其中每个条目是sys中相应条目的增益和相位裕量值。 例如，摆重为100g，长度为2m的模型的增益和相位裕度分别为Gm（1,2）和Pm（1,2）。