粒子群算法及其改进算法

标准粒子群算法及其改进算法

首先在这里介绍一下，这个里主要介绍粒子群算法以及一个改进的二阶振荡粒子群算法。

原理

粒子群优化（PSO）算法是Kennedy和Eberhart受 鸟群群体运动的启发于1995年提出的一种新的群智能优化算法[1]。大概的意思就是一片森林里有一群鸟在找一块食物，它们不知道食物具体在哪，但是可以通过感官（例如嗅觉）去察觉到自己当前位置距离食物的远近。鸟可以记住自己走过的位置并且知道自己做过的最优位置。这一群鸟的运动都是随机的，这类似于一种穷举法。

标准粒子群算法

粒子群算法一般用来找一个函数的最优值。这个函数一般就是适应度函数。
函数中未知量的个数就是这个查找的空间维度。

假设有N个粒子组成一个种群S

Xi是代表粒子i所在的位置，i=1，2，…，N

Vi代表粒子i在位置Xi处的速度，i=1，2，…，N

pi是记录粒子i到走过的最优位置，i=1,2，…，N

pg是所有粒子走过的最优的位置，i=1,2，…，N

w 为惯性权重

c1 、 c2 为学习因子

r1,r2为[ 0 , 1 ]之间均匀分布的参数

接下来种群中每个粒子按照公式更新速度和位置：

Vi( t +1 ) =w * Vi( t ) + c1 * r1 * (pi - xi( t ) ) + c2 * r2 * ( pg - xi( t ) ) （1）
xi( t + 1 ) = xi( t ) + vi( t + 1 ) （2）

PS：这里的r1、r2是每一步迭代都需要更新的随机数
c1、c2和w =则是一开始给定的一些参数，至于参数的给定取决于你自己每次测试这个程序所得到的经验–即哪些参数你跑出的结果比较好就选择哪些参数。
在这里再插一句，在我的实践中认为没有必要去限制迭代过程中速度和位置是否超过最大值，如果在给定区间内存在最优值那么最后还是会迭代回来。只需要在给定的区间内初始化就OK了。在我最开始的测试过程中限制速度和位置是使程序变慢了的，但是我一开始的思路出了问题，到很后面才改正过来也么有再去测试这个，所以就不加评论了。

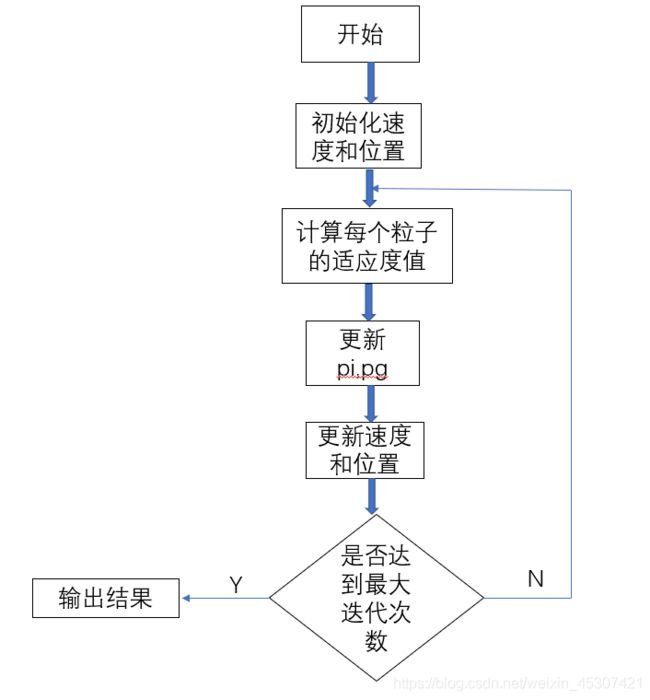
算法流程

标准PSO算法代码

function [xm,fv]=Pso(N,c1,c2,w,M,D)
%c1:自我学习因子
%c2:社会学习因子

%w:惯性权重
%N:种群数量`
%M:最大迭代次数
%D:维数

%初始化种群、速度和位置
tic
for i=1:N
for j=1:D
x(i,j)=unifrnd(-10,10);
v(i,j)=unifrnd(-10,10);
end
end

%根据适应度计算适应度值,初始化pi和pg
for i=1:N
y(i)=test(x(i,:));
pi(i,:)=x(i,:); %y(i,:)为最优位置
end
k = find( y == min(y) ) ;
pg=x(k(1), : ) ;
%更新位置与速度
for t=1:M
for i=1:N
v(i,:)=wv(i,:)+c1rand*(pi(i,:)-x(i,:))+c2rand(pg-x(i,:));
x(i,:)=x(i,:)+v(i,:);
if test(x(i,:)) y(i)=test(x(i,:));
pi(i,:)=x(i,:);
end
if y(i) pg=pi(i,:);
end
end
pbest(t)=test(pg);
end

%输出结果
disp(‘最优位置’);
xm=pg
disp(‘最优值’);
fv=test(pg)
plot(pbest)
toc

test函数–就是适应度函数

function y = test( V )
y=0;
b=length(V);
for i=1:b
y=y+i*V(i)^2;
end

标准粒子群算法的局限性

为进一步说明标准粒子群算法的局限性，做如下推理：
设 φ1=c1*r1 ，φ2=c2r2 ，w=1，由式（1）、（2）可转化 为式（3）、（4）：
Vi( t+1) =Vi( t) +φ1(pi -xi(t))+φ2(pg -xi(t)) （3）
xi(t+1)=xi(t)+vi(t+1) （4）
已知速度公式Vi+1=Vi +a×Δt ，可得： a=φ1(pi -xi(t))+φ2(pg -xi(t))=xi(t)″ （5）
化简可得： xi(t)″+(φ1+φ2)xi(t)-(φ1pi +φ2pg)=0 （6）
式（6）是二阶微分方程，通过二阶微分方程求解公式，求得搜索位置在 t 代的 x(t)的位置路径公式： xi(t)=C1 cos( φ1+φ2t)+C2 sin( φ1+φ2t) （7）
由式（7）可知，xi(t) 在一个固定区间内波动，即在 该区间中寻找每个粒子第 t 次迭代后的位置，位置函数 xi(t) 没有振荡收敛，算法容易陷入局部最优。
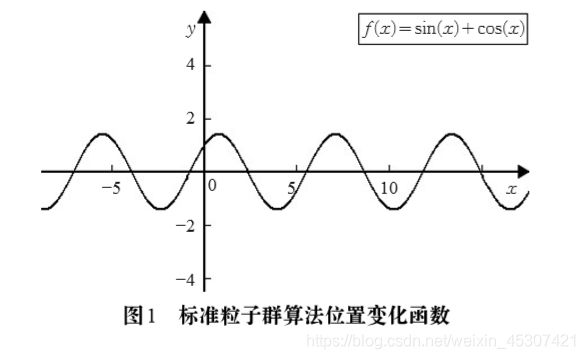
例如，令 C1=1,C2=1, φ1+φ2 =1 ，可得位置函数 xi(t)=cos(t)+ sin(t)的图像，如图1所示。在该图像中， 对于t∈[ -∞，+∞] ， xi(t) 始终在固定上下限 [- 2, 2] 内范围波动，没有振 荡收敛，容易陷入局部最优。因此，在算法中加入振荡 收敛，是跳出局部最优解，提高粒子群算法搜索性能和精度较有效的方法。[1]

改进标准粒子群算法的思想

胡建秀，曾建潮通过在标准二阶粒子群算法速度迭 代方程中引入二阶振荡环节的方法改进算法，来增加粒 子的多样性，提高算法的全局搜索能力，是改进位置函 数搜索区域较好的改进方法。使用二阶振荡环节后，算法前期具有较强的全局搜索能力，振荡收敛；而在后期强局部搜索，渐近收敛。 该粒子群算法的进化方程如下：
Vi( t+1) =w×Vi( t ) + φ1(pi -(1+ξ1)xi(t)+ξ1xi(t-1))+ φ2(pg -(1+ξ2)xi(t)+ξ2xi(t-1)) （8） xi(t+1)=xi(t)+vi(t+1) （9） 算法振荡收敛：
ξ1<2 φ1 -1 φ1 ，
ξ2<2 φ2 -1 φ2 （10）
算法渐进收敛：
ξ1 ≥2 φ1 -1 φ1 ，
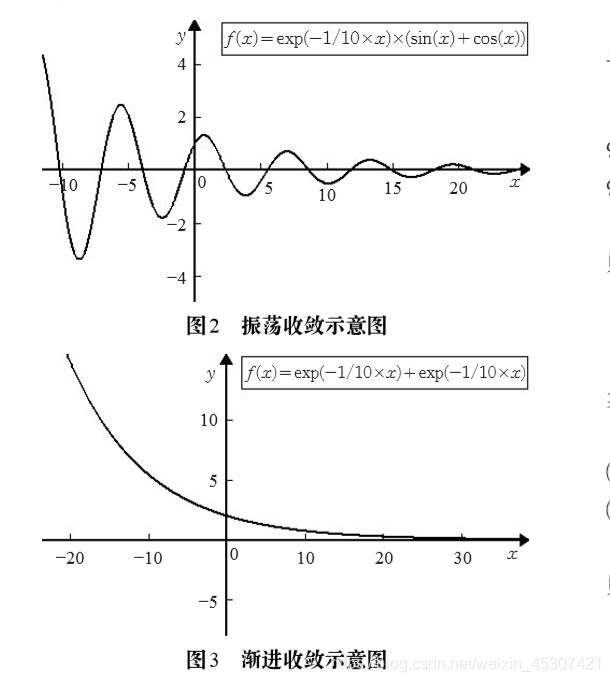
ξ2 ≥2 φ2 -1 φ2 （11） 振荡收敛和渐进收敛示意图如图2和图3所示。[ 1 ]

改进后二阶振荡粒子群算法的迭代公式

Vi( t+1 ) =w×Vi( t ) + φ1(pi -(1+ξ1)xi(t)+ξ2xi(t-1))+ φ2(pg -(1+ξ3)xi(t)+ξ4xi(t-1)) （12） xi(t+1)=xi(t)+vi(t+1)

这个公式的实在上面的二阶振荡粒子群算法的基础上进行的改进，这里ξ虽然是随机数但是取值是有限制的：
设最大迭代次数为Gmax ,
0<ξ2<1+ξ1 2 ,0<ξ4 <1+ξ3 2 ,0<ξ1<1,0<ξ3<1 当 t < Gmax / 2时，
ξ1<ξ2-1,ξ3<ξ4 -1,0<ξ2<1,0<ξ4 <1 当 t > Gmax / 2 时
这么做的意义在于可以时算法在迭代的前半段振荡收敛；
在迭代的后半段使其渐进收敛。
这里的证明和上面的二阶振荡粒子群算法的类似，我这就不展开了，感兴趣的可以自己去找我参考的文献。
PS：关于改进算法的流程图和标准算法的类似，无非就是加了一个迭代次数前一半和后一半参数的改变，这里就不加上去了。

改进二阶振荡粒子群算法代码

function [ z , best ] = PSO_1( w , Gmax ,lizishu , weidu ,a , b )
%这个测试函数的最小值是0，取值范围是[-10 , 10]
% z是最优点的适应值，best是记录最优位置的坐标

%lizishu输入需要的粒子数
%weidu函数的自变量个数
%a下界
%b上界
q=zeros(1,Gmax);
tic
p = inf * ones( 1 , lizishu ) ;%初始的最优解默认为inf
% pg = 0 ;
A = unifrnd( a , b , lizishu , weidu ) ;%A矩阵是位置矩阵，用于储存每一步计算出的位置
B = unifrnd( a , b , lizishu , weidu ) ;%B是速度矩阵，用于储存每一布计算出的V
C = A ;%用于记录每个粒子的最优位置
D = unifrnd( a , b , lizishu , weidu ) ;%位置矩阵，用于记录上一次迭代的位置
c = 2 ; %c通常取1.5 ， 这是一个经验值
y = [] ;%给y申请空间
for i = 1 : lizishu
y = [ y , test( A( i ,: ) ) ] ;
end

for i = 1 : lizishu
if p( i ) > y( i )
C( i , : ) = A( i , : ) ;
end
p( i ) = min( [ p( i ) , y( i ) ] ) ;%更新局部最优解
end

%初始化全局最优解
k = find( p == min( p ) ) ;
pg = C( k( 1 ) , : ) ;
q( i ) = test( pg ) ;

for i = 1 : Gmax
i
r1 = unifrnd( 0 , 1 ) ;
r2 = unifrnd( 0 , 1 ) ;
u1 = r1 * c ;
u2 = r2 * c ;
if i < Gmax / 2
g1 = unifrnd( 0 , 1 ) ; % 这里g1是[ 0 , 1 ]上均匀分布的随机数
g2 = ( 1 + g1 ) / 2 ;
g3 = unifrnd( 0 , 1 ) ;
g4 = ( 1 + g3 ) / 2 ;
for j = 1 : lizishu
B( j , : ) = w * B( j , : ) + u1 * ( C( j , : ) - ( 1 + g1 ) * A( j , : ) + g2 * D( j , : ) ) + u2 * ( pg - ( 1 + g3 ) * A( j , : ) + g4 * D( j , : ) ) ;
D = A ;
A( j , : ) = A( j , : ) + B( j , : ) ;
end
else
g2 = unifrnd( 0 , 1 ) ; % 这里g2是[ 0 , 1 ]上均匀分布的随机数
g1 = ( g2 - 1 ) / 4 ;
g4 = unifrnd( 0 , 1 ) ;
g3 = ( g4 - 1 ) / 4 ;
for j = 1 : lizishu
B( j , : ) = w * B( j , : ) + u1 * ( C( j , : ) - ( 1 + g1 ) * A( j , : ) + g2 * D( j , : ) ) + u2 * ( pg - ( 1 + g3 ) * A( j , : ) + g4 * D( j , : ) ) ;
D = A ;
A( j , : ) = A( j , : ) + B( j , : ) ;
end
end
y = [] ;%下一次迭代前清空y
for j = 1 : lizishu
y = [ y , test( A( j ,: ) ) ] ;
end

   for j = 1 : lizishu
      if p( j ) > y( j )
        C( j , : ) = A( j , : ) ;
      end
        p( j ) = min( [ p( j ) , y( j ) ] ) ;
   end

    k = find( p == min( p ) ) ;%找到最优解的位置
    pg = C( k( 1 ) , : ) ; %保存最优解坐标
    q(i) = test( pg ) ;

end
z = q( Gmax ) ;
best = pg ;
toc
plot(q)

test函数

function y = test( V )
y=0;
b=length(V);
for i=1:b
y=y+i*V(i)^2;
end

两个算法的比较

PS:上面我只给了一个test函数,要测试其他的函数直接更改test函数即可。
下面是两个维度跑出来的结果
1、标准PSO算法：


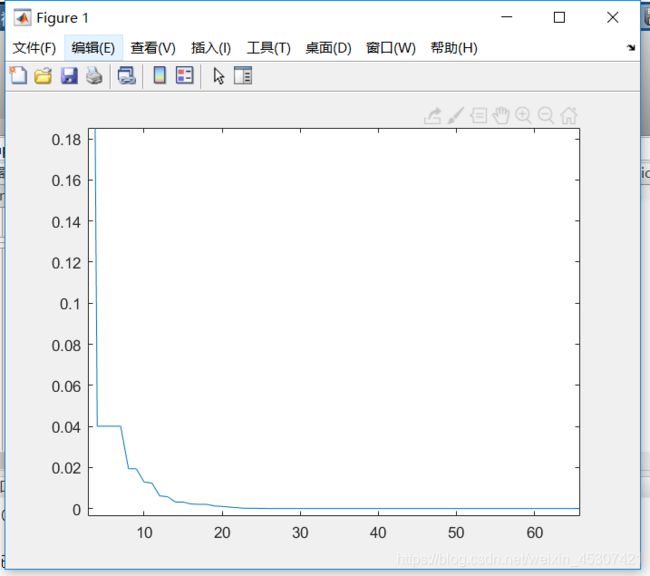
2、改进的二阶振荡PSO算法:

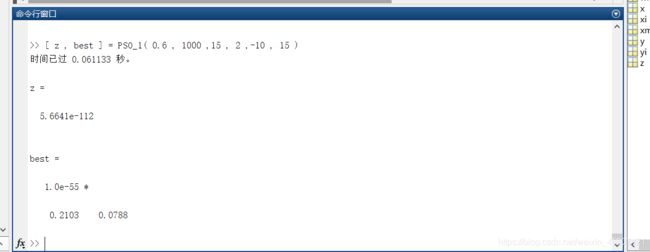
在低维度上这两个算法没有太大差别，改进的算法速度上要稍微快一点。

下面把维度提升到100维：
PS：为了便于观看我改了一下程序，最后都只输出一个最优值。
1、这是标准PSO算法跑出的结果：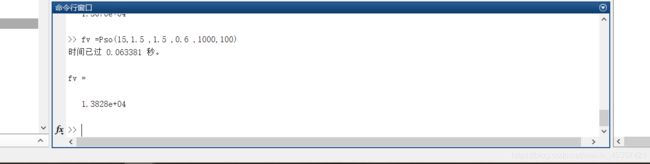
很明显这并没有达到最优值，只是一个局部最优。

2、改进的PSO算法：

可以看到改进的算法的结果在100维下依旧不错，而且很快。

下面我们尝试1000维：
改进的PSO算法结果如下：

我也试过一些最小值是无穷的函数（X^3），以及一些振荡函数(sinx+cosx),都可以跑出结果，这里就不一个个的给出结果了。

PS：因为第一个算法不是我写的原因，是我同学写的我拿来用的，所以两个代码在风格上差别有点大。
这个博客的证明部分基本上我都是从下面的文献里直接拿过来的。
最后如果找出我的错误请告诉我，我会及时改正的。

参考文献

[ 1 ] 蒋丽,叶润周，梁昌勇等，改进的二阶振荡粒子群算法[J]，计算机工程与应用,2009，55（9）：130-139