python机器学习手写算法系列——Gaussian Mixture Model (1d)

本文，就像本系列的其他文章一样。旨在通过阅读原论文+手写代码的方式，自己先把算法搞明白，然后再教其他人。手写代码除了可以验证自己是否搞明白以外，我会对中间过程做图。这样，我可以通过图直观的验证算法是否正确。而这些图，又成为写文章时候的很好的素材。

什么是 Gaussian Mixture Model

GMM，简单的说，真的就是几个Gaussian分布混合在一起。把这些Gaussian分布找出来的过程，就是GMM。一般来说，可以认为GMM是聚类算法，但是scikit-learn把GMM把他放在了mixture模块下面，而不是cluster模块。

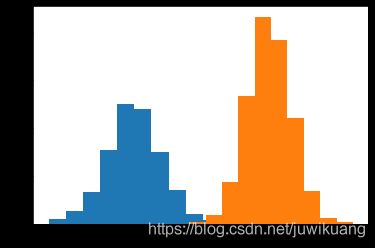
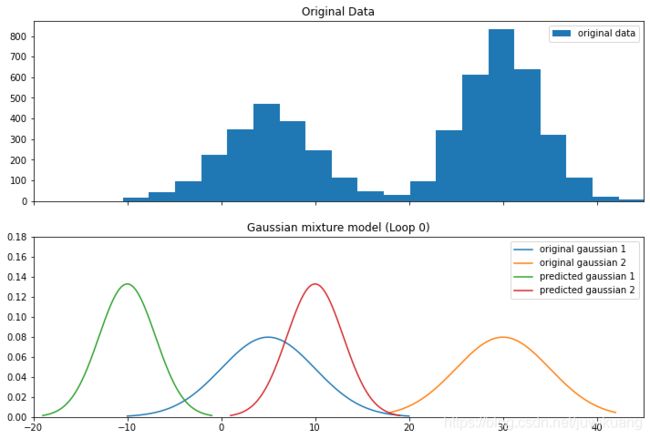
为了模拟数据，我们把两个Gaussian混合在一起。如下图。

EM算法

GMM和KMeans非常类似。

回顾一下KMeans算法，先随机设置几个中心点，然后把这些中心点周围的点聚类成一个簇。再根据簇里的点，重新选择中心点。基本上就是这个套路。

GMM其实也差不多，这里，我们用的是EM算法。EM，就是Estimation和Maximization。

首先，和KMeans一样，需要设立中心点，只不过，这里我们要找出来的，是Gaussian分布。所以，我们这里随机设置两个Gaussian分布，也就是说，我们随机设置两个平均值${\mu }_1,{\mu }_2$和标准差${\sigma }_1,{\sigma }_2$。

Estimation

接着，就是Estimation。我们要估计每一个数据是属于第一个Gaussian分布，还是第二个。估算的方法，就是利用pdf，即Probability Density Function，分别算出一个数据点针对第一个和第二个Gaussian的PDF。如下图所示：

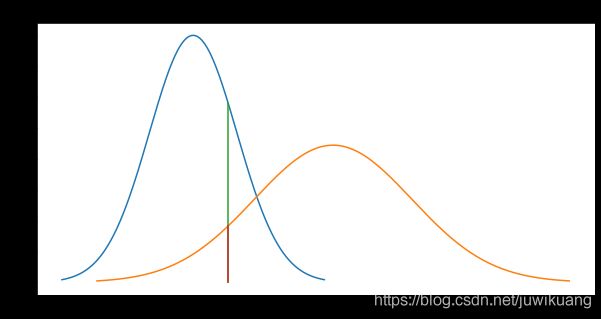
上图中，有两个gaussian分布。我们在9这个地方取一个点。这个点对于蓝色Gaussian的pdf是0.058，而对于黄色Gaussian的pdf是0.018。这是，我们可以用pdf的值，来决定9这个点属于蓝色Gaussian 还是 黄色 Gaussian。所以，这个点属于蓝色的概率是0.058/(0.058+0.018) = 0.76。即这个点76%属于蓝色，24%属于黄色。GMM算法里把这个概率叫做Responsibility，我觉得这里叫权重（weights）比较合适。

def estimate(mix, mu1, sigma1, mu2, sigma2):
    pdf1 = norm.pdf(mix, mu1, sigma1)
    pdf2 = norm.pdf(mix, mu2, sigma2)
    pdf_sum = pdf1 + pdf2
    w1=pdf1/pdf_sum
    w2=pdf2/pdf_sum
    return w1, w2

Maximization

有了权重，下一步就可以根据权重来重新计算$\mu$ 和 $\sigma$。

def maximize(mix, w1, w2):
    mu1=np.average(mix, weights=w1)
    sigma1_squared=np.average((mix-mu1)**2, weights=w1)
    sigma1=np.sqrt(sigma1_squared)
    sigma1
    
    mu2=np.average(mix, weights=w2)
    sigma2_squared=np.average((mix-mu2)**2, weights=w2)
    sigma2=np.sqrt(sigma2_squared)
    sigma2
    
    return mu1, sigma1, mu2, sigma2

测试算法

首先，我们随机确定$\mu$和$\sigma$。

u1 = -10
s1 = 3

u2 = 10
s2 = 3

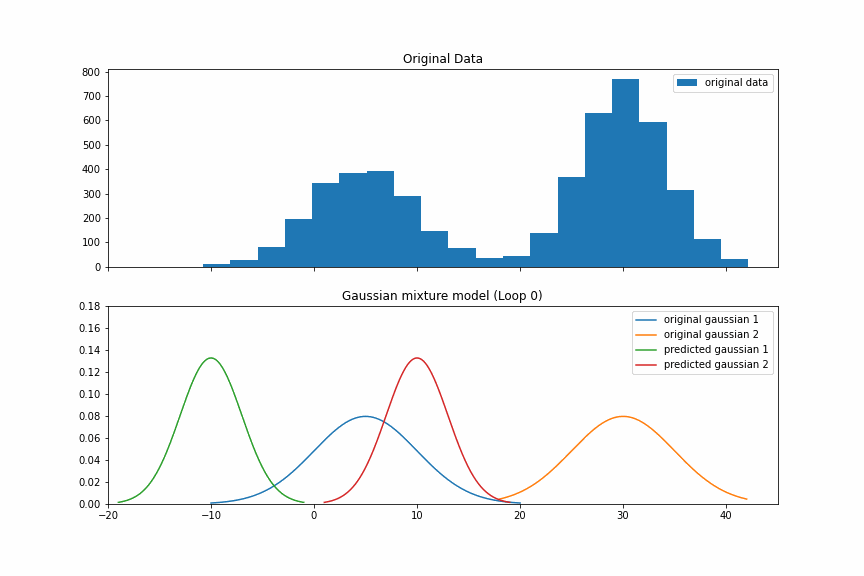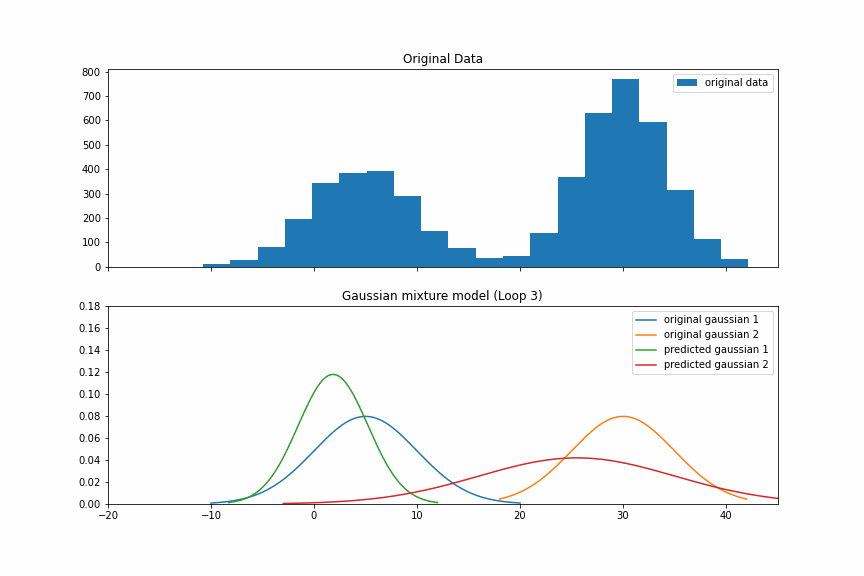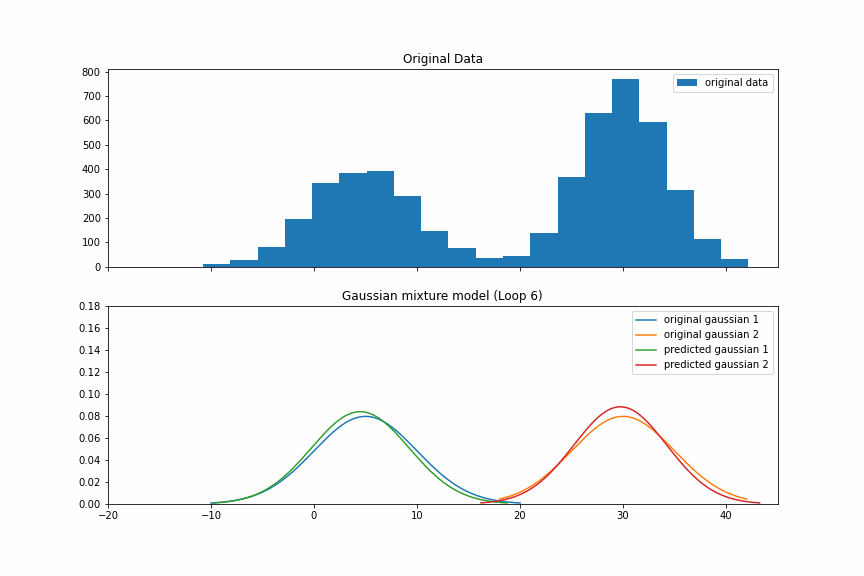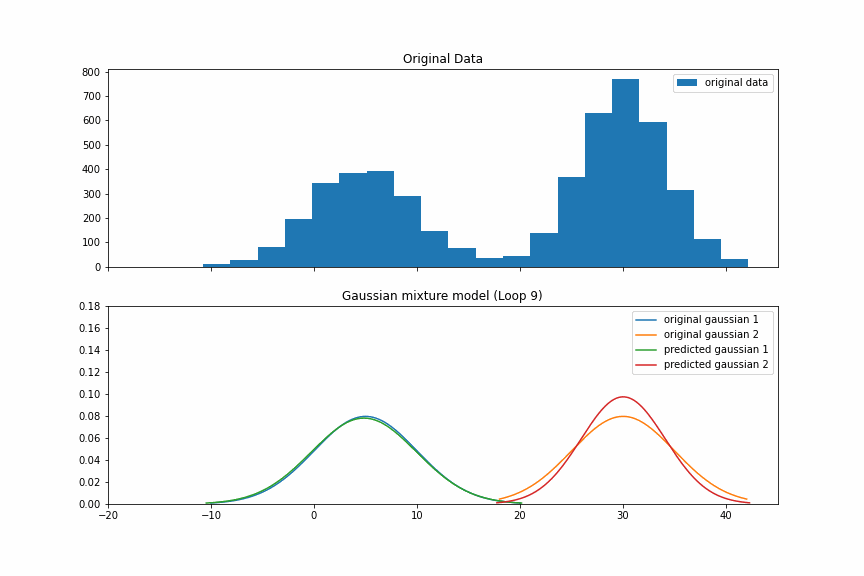
这时，我们得到下图。蓝色和黄色的是原始的Gaussian分布的pdf。绿色和红色的我们的有预测值。

下图是剩下的8次EM过程。我们看到，到第5次迭代的时候，我们的预测值基本上就已经接近真实值了。

GMM in scikit-learn

实际工作中，我们会用scikit-learn来计算GMM。只需要实例化一个GaussianMixture对象，并传入簇（clusters）的个数即可。

clf = mixture.GaussianMixture(n_components=2)
clf.fit(X_train)

具体可自行前往官方网站。

代码

https://github.com/EricWebsmith/machine_learning_from_scrach