神经网络与深度学习(六)——注意力机制
邱锡鹏《神经网络与深度学习》学习笔记。
神经网络与深度学习(六)—— 注意力机制
-
- 1.1 注意力机制
-
- 1.1.1 认知神经学中的注意力
- 1.1.2 注意力机制
-
- 1.1.2.1 注意力分布
- 1.1.2.2 加权平均
- 1.1.3 注意力机制的变体
-
- 1.1.3. 1 键值对注意力
- 1.1.3.2 多头注意力
- 1.1.3.3 结构化注意力
- 1.1.3.4 指针网络
- 1.2 自注意力机制
为了减少计算复杂度,我们引入了局部连接,权重共享以及池化操作来简化网络结构。但目前计算机的计算能力依然是限制神经网络发展的瓶颈。因此我们依然希望在不过度增加模型复杂度(主要是模型参数)的情况下来提高模型的表达能力。
神经网络中可以存储的信息量称为网络容量(Network Capacity)。一般来讲神经网络的存储容量和神经元的数量以及网络的复杂度成正比。
我们可以借鉴人脑解决输入信息过载的机制,从两个方面来提高神经网络处理信息的能力:
- 注意力机制。通过自上而下的信息选择机制来过滤掉大量的无关信息;
- 外部记忆。引入额外的外部记忆,优化神经网络结构来提高网络存储信息的容量。
本文仅探讨注意力机制。
1.1 注意力机制
在计算能力有限的情况下,Attention Mechanism 作为资源分配方案,是解决信息超载问题的主要手段。
一个非常有助于理解的链接:深度学习中的注意力模型。
1.1.1 认知神经学中的注意力
大脑从大量的输入信息中,重点关注一小部分有用的信息同时忽略其他信息的选择能力,叫做注意力 (Attention)。
大脑的注意力一般分为两种:
- 聚焦式注意力(Focus Attention)。有预定目标、依赖任务的、主动有意识的聚焦于某一对象的注意力。
- 基于显著性的注意力(Saliency Based Attention)。由外界刺激驱动的注意力,不需要主动干预,也和任务无关。如果一个对象的刺激信息不同于其周围信息,一种无意识的“赢者通吃(Winner-Take-All)”或者门控机制(Gating)就可以把注意力转向这个对象。
目前的神经网络模型中最大池化(Max Pooling)、门控机制(Gating)近似可以看做基于显著性的注意力机制。
1.1.2 注意力机制
此处注意力机制指主动的聚焦式注意力。
用 X = [ x 1 , ⋯ , x N ] ∈ R D × N \boldsymbol{X}=\left[\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}\right] \in \mathbb{R}^{D \times N} X=[x1,⋯,xN]∈RD×N表示 N N N 组输入信息,其中 D D D维向量 x n ∈ R D , n ∈ [ 1 , N ] \boldsymbol{x}_{n}\in\mathbb{R}^{D},n\in[1,N] xn∈RD,n∈[1,N]表示一组输入信息。为了节省计算资源,只需要从 X \boldsymbol{X} X 中选择一些和任务相关的信息。
注意力机制的计算可以分为两步:
- 在所有输入信息上计算注意力分布,
- 根据注意力分布计算输入信息的加权平均。
1.1.2.1 注意力分布
为了从 N N N 个输入向量 [ x 1 , ⋯ , x N ] [\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}] [x1,⋯,xN]中选择出和某个特定任务相关的信息,我们需要引入一个和任务相关的表示,称为查询向量(Query Vector)。并通过一个打分函数来计算每个输入向量和查询向量之间的相关性。
给定一个和任务相关的查询向量 q \boldsymbol{q} q(查询向量可以是动态生成的,也可以是可学习的参数),我们用注意力变量 z ∈ [ 1 , N ] z\in[1,N] z∈[1,N]来表示被选择信息的索引位置,即 z = n z=n z=n 表示选择了第 n n n个输入向量。为了方便计算,我们采用一种“软性”的信息选择机制。首先计算在给定 q \boldsymbol{q} q和 X \boldsymbol{X} X下,选择第 i i i个输入向量的概率 α n \alpha_n αn:
α n = p ( z = n ∣ X , q ) = softmax ( s ( x n , q ) ) = exp ( s ( x n , q ) ) ∑ j = 1 N exp ( s ( x j , q ) ) \begin{aligned} \alpha_{n} &=p(z=n \mid \boldsymbol{X}, \boldsymbol{q}) \\ &=\operatorname{softmax}\left(s\left(\boldsymbol{x}_{n}, \boldsymbol{q}\right)\right) \\ &=\frac{\exp \left(s\left(\boldsymbol{x}_{n}, \boldsymbol{q}\right)\right)}{\sum_{j=1}^{N} \exp \left(s\left(\boldsymbol{x}_{j}, \boldsymbol{q}\right)\right)} \end{aligned} αn=p(z=n∣X,q)=softmax(s(xn,q))=∑j=1Nexp(s(xj,q))exp(s(xn,q))
其中 α n \alpha_{n} αn称为注意力分布(Attention Distribution), s ( x n , q ) s\left(\boldsymbol{x}_{n}, \boldsymbol{q}\right) s(xn,q)为注意力打分函数(s即similarity,计算两者的相似性或者相关性),可以使用以下几种方式来计算:
- 加性模型: s ( x , q ) = v ⊤ tanh ( W x + U q ) s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{v}^{\top} \tanh (\boldsymbol{W} \boldsymbol{x}+\boldsymbol{U} \boldsymbol{q}) s(x,q)=v⊤tanh(Wx+Uq)
- 点积模型: s ( x , q ) = x T q s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\text{T}}\boldsymbol{q} s(x,q)=xTq
- 缩放点积模型: s ( x , q ) = x ⊤ q D s(\boldsymbol{x}, \boldsymbol{q})=\frac{\boldsymbol{x}^{\top} \boldsymbol{q}}{\sqrt{D}} s(x,q)=Dx⊤q
- 双线性模型: S ( x , q ) = x ⊤ W q S(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top} \boldsymbol{W} \boldsymbol{q} S(x,q)=x⊤Wq
其中 W \boldsymbol{W} W, U \boldsymbol{U} U, v \boldsymbol{v} v 为可学习的参数, D D D为输入向量的维度。
理论上加性模型和点积模型的复杂度差不多,但点积模型可以更好的利用矩阵乘积,计算效率更高。
当输入向量的维度较高时,点积模型的值通常由较大的方差,从而导致 Softmax 函数的梯度会比较小。而缩放点积模型可以较好的解决这个问题。
双线性模型是一种泛化的点积模型,假设模型参数 W = U T V \boldsymbol{W}=\boldsymbol{U}^T\boldsymbol{V} W=UTV,双线性模型可写为 s ( x , q ) = x ⊤ U ⊤ V q = ( U x ) ⊤ ( V q ) s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top} \boldsymbol{U}^{\top} \boldsymbol{V} \boldsymbol{q}=(\boldsymbol{U} \boldsymbol{x})^{\top}(\boldsymbol{V} \boldsymbol{q}) s(x,q)=x⊤U⊤Vq=(Ux)⊤(Vq),即分别对 x \boldsymbol{x} x, q \boldsymbol{q} q进行线性变换后计算点积。相比点积模型,双线性模型在计算相似度时引入了非对称性。
1.1.2.2 加权平均
注意力分布 α n \alpha_n αn可以解释为在给定任务相关的查询 q \boldsymbol{q} q时,第 n n n个输入向量受关注的程度。我们采用一种“软性”的信息选择机制对输入信息进行汇总,即软性注意力机制(Soft Attention Mechanism):
att ( X , q ) = ∑ n = 1 N α n x n = E z ∼ p ( z ∣ X , q ) [ x z ] \begin{aligned} \operatorname{att}(\boldsymbol{X}, \boldsymbol{q}) &=\sum_{n=1}^{N} \alpha_{n} \boldsymbol{x}_{n} \\ &=\mathbb{E}_{z \sim p(z \mid \boldsymbol{X}, \boldsymbol{q})}\left[\boldsymbol{x}_{z}\right] \end{aligned} att(X,q)=n=1∑Nαnxn=Ez∼p(z∣X,q)[xz]
软性注意力机制选择的信息是所有输入向量在注意力分布下的期望。
另一种注意力是只关注某一输入向量,叫作硬性注意力(Hard Attention)。硬性注意力有两种实现方式:
1)选取注意力分布中概率最高的输入向量,即最大采样:
att ( X , q ) = x n ^ \operatorname{att}(\boldsymbol{X}, \boldsymbol{q})=\boldsymbol{x}_{\hat{n}} att(X,q)=xn^
其中 n ^ \hat{n} n^为概率最大的输入向量的下标,即 n ^ = arg max n = 1 N α n \hat{n}={\arg \max}^{N}_{n=1} \alpha_{n} n^=argmaxn=1Nαn。
2)在注意力分布式上随机采样。
硬性注意力的一个缺点是损失函数与注意力分布之间的函数关系不可导,无法使用反向传播算法进行训练。因此硬性注意力通常使用强化学习来进行训练。
注意力机制可以单独使用,但更多的是作为神经网络中的一个组件。
1.1.3 注意力机制的变体
1.1.3. 1 键值对注意力
用键值对(key-velue pair)格式表示输入信息,其中“键”用来计算注意力分布 α n \alpha_n αn,“值”用来计算聚合信息。
用 ( K , V ) = [ ( k 1 , v 1 ) , ⋯ , ( k N , v N ) ] (\boldsymbol{K}, \boldsymbol{V})=\left[\left(\boldsymbol{k}_{1}, \boldsymbol{v}_{1}\right), \cdots,\left(\boldsymbol{k}_{N}, \boldsymbol{v}_{N}\right)\right] (K,V)=[(k1,v1),⋯,(kN,vN)]表示 N N N组输入信息,给定任务相关的查询向量 q \boldsymbol{q} q时,注意力函数为:
att ( ( K , V ) , q ) = ∑ n = 1 N α n v n = ∑ n = 1 N exp ( s ( k n , q ) ) ∑ j exp ( s ( k j , q ) ) v n \begin{aligned} \operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}) &=\sum_{n=1}^{N} \alpha_{n} \boldsymbol{v}_{n} \\ &=\sum_{n=1}^{N} \frac{\exp \left(s\left(\boldsymbol{k}_{n}, \boldsymbol{q}\right)\right)}{\sum_{j} \exp \left(s\left(\boldsymbol{k}_{j}, \boldsymbol{q}\right)\right)} \boldsymbol{v}_{n} \end{aligned} att((K,V),q)=n=1∑Nαnvn=n=1∑N∑jexp(s(kj,q))exp(s(kn,q))vn
当 K = V \boldsymbol{K}=\boldsymbol{V} K=V时,键值对模式就等价于普通的注意力机制。
1.1.3.2 多头注意力
Multi-Head Attention 是利用多个查询 Q = [ q 1 , ⋯ , q M ] \boldsymbol{Q}=\left[\boldsymbol{q}_{1}, \cdots, \boldsymbol{q}_{M}\right] Q=[q1,⋯,qM]来并行地从输入信息中选取多组信息,每个注意力关注输入信息的不同部分。
att ( ( K , V ) , Q ) = att ( ( K , V ) , q 1 ) ⊕ ⋯ ⊕ att ( ( K , V ) , q M ) \operatorname{att}((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{Q})=\operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_{1}\right) \oplus \cdots \oplus \operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_{M}\right) att((K,V),Q)=att((K,V),q1)⊕⋯⊕att((K,V),qM) ⊕ \oplus ⊕表示向量拼接。
1.1.3.3 结构化注意力
1.1.3.4 指针网络
注意力机制主要用来做信息筛选,从输入信息中选取相关的信息。
指针网络(Pointer Network)是一种序列到序列模型,输入是长度为 N N N的向量序列 X = [ x 1 , ⋯ , x N ] \boldsymbol{X}=\left[\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}\right] X=[x1,⋯,xN],输出是长度为 M M M的下标序列 c 1 : M = c 1 , c 2 , ⋯ , c M , c m ∈ [ 1 , N ] , ∀ m \boldsymbol{c}_{1: M}=c_{1}, c_{2}, \cdots, c_{M}, c_{m} \in[1, N], \forall m c1:M=c1,c2,⋯,cM,cm∈[1,N],∀m
和一般的序列到序列的任务不同,这里的输出序列是输入序列的下标(索引)。比如输入一组乱序的数字,输出为按大小排序的输入数字序列的下标。如输入 20,5,10,输出 1,3,2。
条件概率 p ( c 1 : M ∣ x 1 : N ) p\left(c_{1: M} \mid \boldsymbol{x}_{1: N}\right) p(c1:M∣x1:N)可以写为
p ( c 1 : M ∣ x 1 : N ) = ∏ m = 1 M p ( c m ∣ c 1 : ( m − 1 ) , x 1 : N ) ≈ ∏ m = 1 M p ( c m ∣ x c 1 , ⋯ , x c m − 1 , x 1 : N ) \begin{aligned} p\left(c_{1: M} \mid \boldsymbol{x}_{1: N}\right) &=\prod_{m=1}^{M} p\left(c_{m} \mid c_{1:(m-1)}, \boldsymbol{x}_{1: N}\right) \\ & \approx \prod_{m=1}^{M} p\left(c_{m} \mid \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{m-1}}, \boldsymbol{x}_{1: N}\right) \end{aligned} p(c1:M∣x1:N)=m=1∏Mp(cm∣c1:(m−1),x1:N)≈m=1∏Mp(cm∣xc1,⋯,xcm−1,x1:N)其中条件概率 p ( c m ∣ x c 1 , ⋯ , x c m − 1 , x 1 : N ) p\left(c_{m} \mid \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{m-1}}, \boldsymbol{x}_{1: N}\right) p(cm∣xc1,⋯,xcm−1,x1:N)可以通过注意力分布来计算。假设用一个循环神经网络对 x c 1 , ⋯ , x c m − 1 , x 1 : N \boldsymbol{x}_{c_{1}}, \cdots, \boldsymbol{x}_{c_{m-1}}, \boldsymbol{x}_{1: N} xc1,⋯,xcm−1,x1:N进行编码得到向量 h m \boldsymbol{h}_m hm,则
p ( c m ∣ c 1 : ( m − 1 ) , x 1 : N ) = softmax ( s m , n ) p\left(c_{m} \mid c_{1:(m-1)}, x_{1: N}\right)=\operatorname{softmax}\left(s_{m, n}\right) p(cm∣c1:(m−1),x1:N)=softmax(sm,n)
其中 s m , n s_{m,n} sm,n为在解码过程的第 m m m步时, h m \boldsymbol{h}_m hm对 h n \boldsymbol{h}_n hn的未归一化的注意力分布,即
s m , n = v ⊤ tanh ( W x n + U h m ) , ∀ n ∈ [ 1 , N ] s_{m, n}=\boldsymbol{v}^{\top} \tanh \left(\boldsymbol{W} \boldsymbol{x}_{n}+\boldsymbol{U} \boldsymbol{h}_{m}\right), \forall n \in[1, N] sm,n=v⊤tanh(Wxn+Uhm),∀n∈[1,N]
其中 v \boldsymbol{v} v, W \boldsymbol{W} W, U \boldsymbol{U} U为可学习的参数。
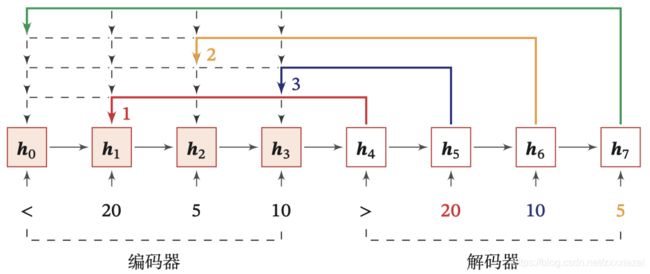
下图给出了指针网络的实例,其中 h 1 \boldsymbol{h}_1 h1, h 2 \boldsymbol{h}_2 h2, h 3 \boldsymbol{h}_3 h3为输入数字 20,5,10 经过循环神经网络的隐状态, h 0 \boldsymbol{h}_0 h0对应特殊字符‘<’.当输入‘>’时,网络一步一步输出桑输入数字从大到小排列的下标。
1.2 自注意力机制
虽然循环网络理论上可以建立长距离依赖关系,但由于信息传递的容量以及梯度消失问题,实际上也只能建立短距离依赖关系。
如果要建立序列之间的长距离依赖关系,可以使用以下两种方法:
1)增加物理的层数,通过一个深层网络来获取远距离的信息交互;
2)使用全连接网络。
全连接网络是一种非常直接的建模远距离依赖的模型,但是无法处理变长的输入序列,不同的输入长度,其连接权重的大小也不同。这时我们可以利用注意力机制来“动态”的生成不同连接的权重,这就是自注意力模型(self-attention model)。自注意力模型更容易捕获中长距离的相互依赖关系。
为提高模型能力,自注意力模型经常采用查询-键-值(query-key-velue,QKV)模式,其计算过程如下图所示,其中红色字母表示矩阵的维度。

假设输入序列为 X = [ x 1 , ⋯ , x N ] ∈ R D x × N \boldsymbol{X}=\left[\boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{N}\right] \in \mathbb{R}^{D_{x} \times N} X=[x1,⋯,xN]∈RDx×N,输出序列为 H = [ h 1 , ⋯ , h N ] ∈ R D v × N \boldsymbol{H}=\left[\boldsymbol{h}_{1}, \cdots, \boldsymbol{h}_{N}\right] \in \mathbb{R}^{D_{v} \times N} H=[h1,⋯,hN]∈RDv×N,自注意力模型的具体计算过程如下:
1)对于每个输入 x i \boldsymbol{x}_{i} xi,我们首先将其线性映射到三个不同的空间,得到查询向量KaTeX parse error: Expected '}', got 'EOF' at end of input: …athbb{R}^{D_{k}、键向量 k i ∈ R D k \boldsymbol{k}_{i} \in \mathbb{R}^{D_{k}} ki∈RDk和值向量 v i ∈ R D v \boldsymbol{v}_{i} \in \mathbb{R}^{D_{v}} vi∈RDv。
对于整个输入序列 X \boldsymbol{X} X,线性映射过程可以简写为 Q = W q X ∈ R D k × N K = W k X ∈ R D k × N V = W v X ∈ R D v × N \begin{array}{l}\boldsymbol{Q}=\boldsymbol{W}_{q} \boldsymbol{X} \in \mathbb{R}^{D_{k} \times N} \\ \boldsymbol{K}=\boldsymbol{W}_{k} \boldsymbol{X} \in \mathbb{R}^{D_{k} \times N} \\ \boldsymbol{V}=\boldsymbol{W}_{v} \boldsymbol{X} \in \mathbb{R}^{D_{v} \times N}\end{array} Q=WqX∈RDk×NK=WkX∈RDk×NV=WvX∈RDv×N
其中 W q ∈ R D k × D x , W k ∈ R D k × D x , W v ∈ R D v × D x \boldsymbol{W}_{q} \in \mathbb{R}^{D_{k} \times D_{x}}, \boldsymbol{W}_{k} \in \mathbb{R}^{D_{k} \times D_{x}}, \boldsymbol{W}_{v} \in \mathbb{R}^{D_{v} \times D_{x}} Wq∈RDk×Dx,Wk∈RDk×Dx,Wv∈RDv×Dx分别为线性映射的参数矩阵, Q = [ q 1 , ⋯ , q N ] , K = [ k 1 , ⋯ , k N ] , V = [ v 1 , ⋯ , v N ] \boldsymbol{Q}=\left[\boldsymbol{q}_{1}, \cdots, \boldsymbol{q}_{N}\right], \boldsymbol{K}=\left[\boldsymbol{k}_{1}, \cdots, \boldsymbol{k}_{N}\right], \boldsymbol{V}=\left[\boldsymbol{v}_{1}, \cdots, \boldsymbol{v}_{N}\right] Q=[q1,⋯,qN],K=[k1,⋯,kN],V=[v1,⋯,vN]分别由查询向量、键向量和值向量构成的矩阵。
2)对于每一个查询向量 q n \boldsymbol{q}_{n} qn利用键值对注意力机制,可以得到输出 h n \boldsymbol{h}_{n} hn
h n = att ( ( K , V ) , q n ) = ∑ j = 1 N α n j v j = ∑ j = 1 N softmax ( s ( k j , q n ) ) v j \begin{aligned} \boldsymbol{h}_{n} &=\operatorname{att}\left((\boldsymbol{K}, \boldsymbol{V}), \boldsymbol{q}_{n}\right) \\ &=\sum_{j=1}^{N} \alpha_{n j} \boldsymbol{v}_{j} \\ &=\sum_{j=1}^{N} \operatorname{softmax}\left(s\left(\boldsymbol{k}_{j}, \boldsymbol{q}_{n}\right)\right) \boldsymbol{v}_{j} \end{aligned} hn=att((K,V),qn)=j=1∑Nαnjvj=j=1∑Nsoftmax(s(kj,qn))vj
其中 n , j ∈ [ 1 , N ] n,j\in[1,N] n,j∈[1,N]为输出和输入向量序列的位置, α n j \alpha_{nj} αnj表示第 n n n个输出关注到第 j j j个输入的权重。
如果使用缩放点积来作为注意力打分函数,输出向量序列可以简写为
H = V softmax ( K ⊤ V D k ) \boldsymbol{H}=\boldsymbol{V} \operatorname{softmax}\left(\frac{\boldsymbol{K}^{\top} \boldsymbol{V}}{\sqrt{D_{k}}}\right) H=Vsoftmax(DkK⊤V)
其中 softmax(·)为按列进行归一化的函数。
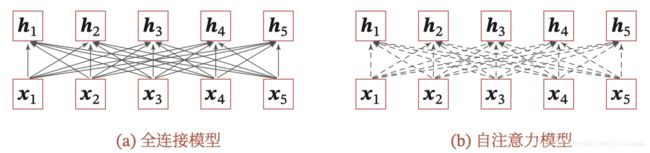
下图为全连接模型和自注意力模型的对比,实线表示可学习的权重,虚线表示动态生成的权重。由于自注意力模型的权重是动态生成的,因此可以处理变成的信息序列。
一个有助于理解的延伸阅读:详解Transformer (Attention Is All You Need)。

