中科大-凸优化 笔记(lec18)-拟凸函数(上)
全部笔记的汇总贴(视频也有传送门):中科大-凸优化
一、凸集与凸函数的关系
α − s u b l e v e l s e t \alpha - sublevel\;set α−sublevelset
若 f : R n → R f:\R^n\rightarrow\R f:Rn→R,定义其 α − s u b l e v e l s e t \alpha - sublevel\;set α−sublevelset为 C α = { x ∈ d o m f ∣ f ( x ) ≤ α } C_\alpha=\{x\in dom\;f|f(x)\le\alpha\} Cα={ x∈domf∣f(x)≤α}
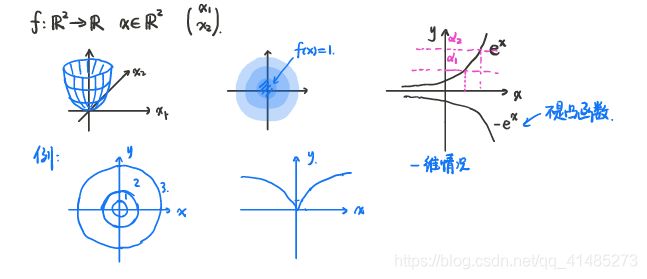
凸函数的所有的 α − s u b l e v e l s e t \alpha - sublevel\;set α−sublevelset都是凸集。
证明: ∀ x , y ∈ C α , f ( x ) ≤ α , f ( y ) ≤ α , x ∈ d o m f , y ∈ d o m f f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) ≤ θ α + ( 1 − θ ) α = α θ x + ( 1 − θ ) y ∈ C α \forall x,y\in C_\alpha,f(x)\le\alpha,f(y)\le\alpha,x\in dom\;f,y\in dom\;f\\f(\theta x+(1-\theta)y)\le\theta f(x)+(1-\theta)f(y)\\\le\theta \alpha+(1-\theta)\alpha\\=\alpha\\\theta x+(1-\theta)y\in C_\alpha ∀x,y∈Cα,f(x)≤α,f(y)≤α,x∈domf,y∈domff(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)≤θα+(1−θ)α=αθx+(1−θ)y∈Cα
若函数的 α − s u b l e v e l s e t \alpha - sublevel\;set α−sublevelset都是凸集,则 f f f不一定是凸函数。
二、拟凸函数(Quasi Convex Function)
f : R n → R f:\R^n\rightarrow\R f:Rn→R
Q u a s i C o n v e x : S α = { x = d o m f ∣ f ( x ) ≤ α } 凸 , ∀ α Q u a s i C o n c a v e : S α ′ = { x = d o m f ∣ f ( x ) ≥ α } 凸 , ∀ α Q u a s i L i n e a r : S α ′ ′ = { x = d o m f ∣ f ( x ) = α } 凸 , ∀ α Quasi\;Convex :S_\alpha=\{x=dom\;f|f(x)\le\alpha\}\;\;凸,\forall\alpha\\Quasi\;Concave :S'_\alpha=\{x=dom\;f|f(x)\ge\alpha\}\;\;凸,\forall\alpha\\Quasi\;Linear :S''_\alpha=\{x=dom\;f|f(x)=\alpha\}\;\;凸,\forall\alpha QuasiConvex:Sα={ x=domf∣f(x)≤α}凸,∀αQuasiConcave:Sα′={ x=domf∣f(x)≥α}凸,∀αQuasiLinear:Sα′′={ x=domf∣f(x)=α}凸,∀α
y = e x y=e^x y=ex同时满足上面三条性质。
凸 ⇒ \Rightarrow ⇒ 拟凸, \;\;\;\;\;\;\; 拟凸 ⇏ \nRightarrow ⇏凸
也称为单模态函数(Unimodal Function)
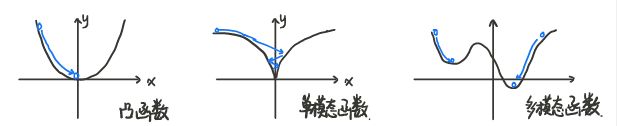
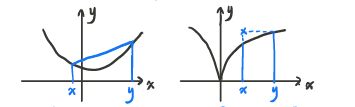
f : R n → R f:\R^n\rightarrow\R f:Rn→R为凸,则 d o m f dom\;f domf为凸, ∀ x , y ∈ d o m f , 0 ≤ θ ≤ 1 \forall x,y\in dom\;f,0\le\theta\le1 ∀x,y∈domf,0≤θ≤1 θ f ( x ) + ( 1 − θ ) f ( y ) ≥ f ( θ x + ( 1 − θ ) y ) \theta f(x)+(1-\theta)f(y)\ge f(\theta x+(1-\theta)y) θf(x)+(1−θ)f(y)≥f(θx+(1−θ)y)
f : R n → R f:\R^n\rightarrow\R f:Rn→R为拟凸,则 d o m f dom\;f domf为凸, ∀ x , y ∈ d o m f , 0 ≤ θ ≤ 1 \forall x,y\in dom\;f,0\le\theta\le1 ∀x,y∈domf,0≤θ≤1 max { f ( x ) , f ( y ) } ≥ f ( θ x + ( 1 − θ ) y ) \max\{f(x),f(y)\}\ge f(\theta x+(1-\theta)y) max{ f(x),f(y)}≥f(θx+(1−θ)y)
例
向量的长度 x ∈ R n x\in\R^n x∈Rn: x x x中最后一个非零元素的位置
f ( x ) = { max { i , x i ≠ 0 } x ≠ 0 0 x = 0 { f ( x ) ≤ α } ⇒ 对 所 有 i = ⌊ α ⌋ + 1 , ⋯ , n , x i = 0 f(x)=\left\{ \begin{array}{l} \max\{i,x_i\neq0\}\;\;\;x\neq0\\ \\0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x=0\end{array} \right. \\\{f(x)\le\alpha\}\Rightarrow 对所有i=\lfloor \alpha\rfloor+1,\cdots,n,x_i=0 f(x)=⎩⎨⎧max{ i,xi=0}x=00x=0{ f(x)≤α}⇒对所有i=⌊α⌋+1,⋯,n,xi=0
例
线性分数函数 f ( x ) = a T x + b c T x + d d o m f = { x ∣ c T x + d > 0 } f(x)=\frac{a^Tx+b}{c^Tx+d}\;\;dom\;f=\{x|c^Tx+d>0\} f(x)=cTx+daTx+bdomf={ x∣cTx+d>0}(不一定凸,但是拟凸)
S α = { x ∣ c T x + d > 0 , a T x + b c T x + d ≤ α } = { x ∣ c T x + d > 0 , a T x + b ≤ α ( c T x + d ) } ( 线 性 不 等 式 ⇒ 多 面 体 ) S_\alpha=\{x|c^Tx+d>0,\frac{a^Tx+b}{c^Tx+d}\le\alpha\}\\=\{x|c^Tx+d>0,a^Tx+b\le\alpha(c^Tx+d)\}\\(线性不等式\Rightarrow多面体) Sα={ x∣cTx+d>0,cTx+daTx+b≤α}={ x∣cTx+d>0,aTx+b≤α(cTx+d)}(线性不等式⇒多面体)
下一章传送门:中科大-凸优化 笔记(lec19)-拟凸函数(下)