线性表

前言：

1月21号的时候我boss打电话给我说要我好好准备一下，因为他帮我联系了阿里和头条的视觉方向的实习。因为面试有机考，于是这个寒假准备好好复习一哈opencv 重温数据结构。
想来DS学完有一年了，但大二那年刚转到计软都没咋开窍。现在刚好有机会搞一波。
用的教材是清华大学的那本数据结构（C语言版），然而我用的是C++来实现 ，没关系，开干吧！

学习目标：

了解线性表的定义，掌握线性表的操作，学会分析时间复杂度（由于是复习DS，时间复杂度不会深究，想仔细学习的话敬请参考算法导论哈）。

---

学习内容：

1、 线性表的定义 2、 线性表的基本操作 3、 时间复杂度分析 4、 LeetCode真题实战

---

线性表定义

如果非要做到concise definition，其就是个“数组”。
那官方一点正式一点的版本呢？一个线性表是一个含有n个数据元素的有限序列。
线性表一个很大的特点就是长度可变的，这决定了我们写代码时保留一些东西会对操作更加友好。说的那么神秘不就是TMD长度吗！！

线性表的基本操作

这里就默认大佬都是精通 C&&Cpp的啦。
根据上述，其实现方式就是数组，操作也是基于数组之上的。
正如数组使用前需要申明一样，如int a[10]，抑或是动态申明的int* a = new int[10]，线性表同样需要一个创建申明的过程。
同时一个线性表需要集成大量的操作，那么用类封装起来吧。
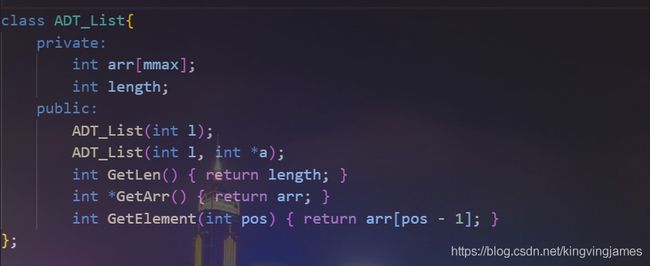
（下图mmax后面修改为1e4，否则会爆栈。出现一个cygwin.S的segmentation fault。）

可以看到这个线性表类的实际内容，与一个普通的数组相比仅仅是多保存了一个长度属性。其初始化方式重载了两种，一是只给长度，值任意设定（不一定和我一样设为0），二则是利用一个数组对其进行初始化（一般为了满足做题的需求，用数组初始化的方式长度是会直接给你的，因此没必要特意求数组大小）。

如此一来，紧接着实现一些简单得不能再简单的功能。

按照教材顺序接下来依次实现的是两个线性表的并集操作，然后是插入保持递减的顺序，最后才是增删操作。

集合的并，emmm，不解释了，上代码：

好吧，思来想去说得详细一点不会有错。首先我们需要两张线性表，那么另外一张以参数形式传入函数。要先取出此表的数组，然后判断此表中的元素是否存在于（*this）表中，不存在则并入。注意：我们并不是直接修改某一张表，而是创建了一张新表，新表长度就是（*this）表的长度加上新并进来的长度。最后展示这张表的结果，运行示意图如下：

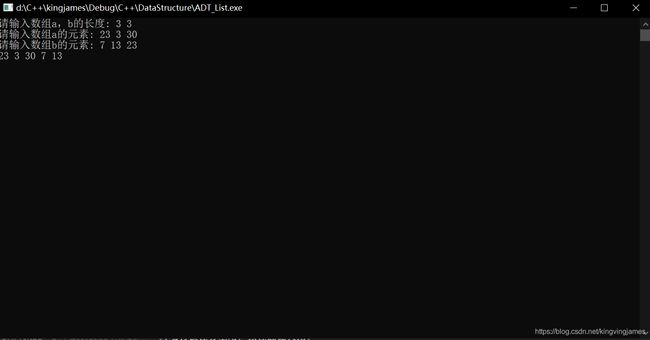
这里要回忆一下某次做题的收获！
想来不少人说Python yyds不无道理，如下所示：
（Attention！！List类型无此属性，即[]不行，只有集合才行，即{}）

好der，那么接下来就是两组递减的线性表，插入后仍呈递减的顺序。
思路图如下所示：

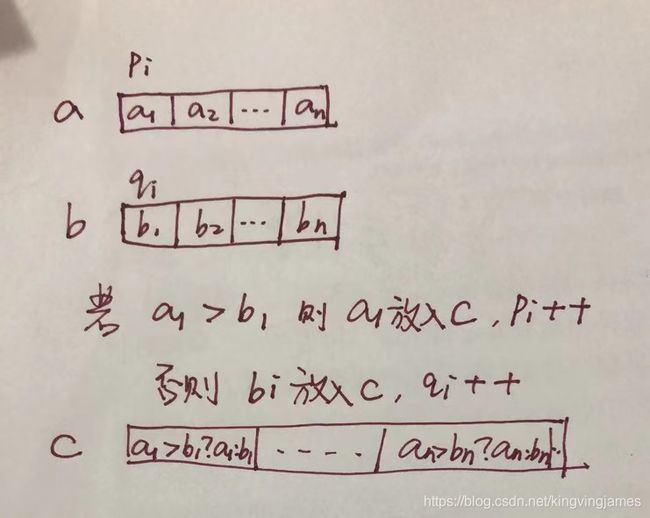
我们同时要考虑的是，假如某一组指针已经移动到末尾了，但另一组却仍没处理完毕的情况。所以在两者进行比较的循环结束后，要外加两个while来把某一组剩余的数全部加入。

运行结果如下：

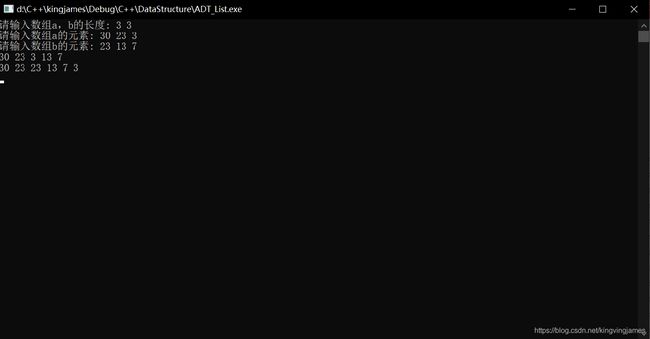
OK！涉及两个线性表的操作就到这了，接下来开始增删了！
诶呀我滴妈，学了一个学期的数据库看到这两个字眼都有点disgusting了！！！
formally，就是insert和delete函数！
两者相通性很强，着重看插入吧。
这里需要明白线性表的存储空间在内存中是连续的。每两个元素间的间距就是size(type_of_element)。现要在一位置插入一个值，那么相应的，处于其之后的所有元素都需要向后移动一个位置。
代码和运行结果如下：

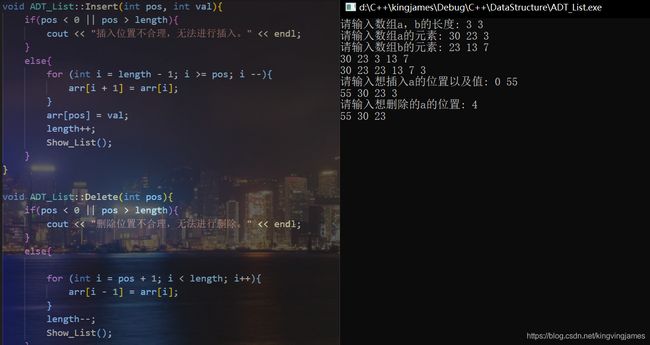
值得一提的是有些OJ上的题目会和此代码有出入，因为有些是不允许0出现的。比如删除位置1，代表的实际上指的是第一个数，相当于下标索引意义上的0。

删除代码同样已经在上方展示，实际上就是逆着插入的来。即删除一个后，其后的所有元素都需要向前移动一个单位。用覆盖的方式来起到删除的作用。

两者都须注意的是，操作成功的话需要改变长度！！！

数组实战

那既然数组如此简单，不妨实战试试。
从LeetCode从易到难筛选三题作为靶子，aim & fire！
[实际上筛选数组标签的题目，会有很多用到其他算法，经典的如买卖股票的动态规划算法等。这些题目已经过滤掉了哈，基本都只涉及简单算法。]

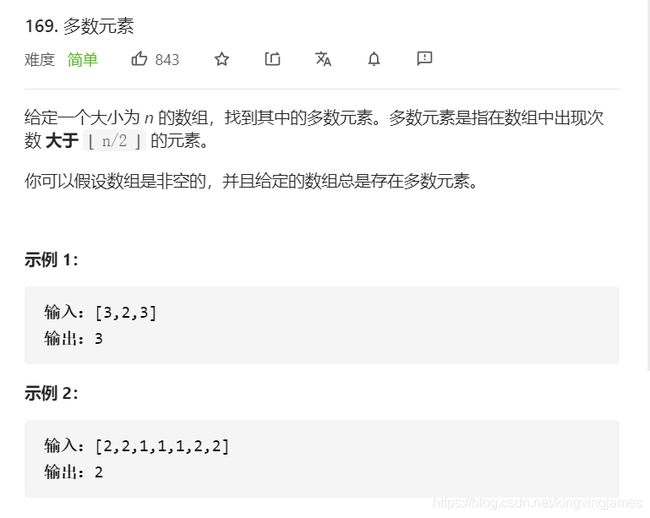
乍一看，豁！好简单的题。（后面还有一个进阶项要求O（n）时间复杂度，O（1）空间复杂度实现未截入）
最先想到的当然就是，用双重循环，第一重选取到此数组的第i个数，第二重循环就是统计次数出现次数。
易知，时间复杂度为O(n²)。啊，测试是超时的！！！
本菜鸡也不愿多想，改进了一小点，是这样的。

class Solution {
     
public:
    int majorityElement(vector<int>& nums) {
     
        sort(nums.begin(), nums.end());
        return nums[nums.size() / 2];
    }
};

sort是algorithm头文件自带的排序函数，其时间复杂度是O(nlogn)，为啥嘞？放到排序模块讲，那儿会涉及到比较高效的堆排序，快速排序就是此时间复杂度。
待排序完毕后我们只要取中值此值就必然是满足要求的。应该不难理解，一个数倘若出现次数超过了半长，那么中间位置一定是被其占据的。反证法，如果一个数组的中间位置不是那个出现了半长多（超过 n/2）的数字，那么那个数字至多只能出现半长的次数，说明原假设成立的。

那么如何进行optimization呢？
这里隆重介绍一个极具灵性的算法—Boyer-Moore 投票算法。
emmm，直接上官方的解释文档吧，然后自己再思考翻译一遍

那代码实现方式实际上也是按部就班，如下所示：

class Solution {
     
public:
    int majorityElement(vector<int>& nums) {
     
        int candidate = nums[0];
        int cnt = 0;
        for(int i = 0 ; i < nums.size() ; i ++){
     
            if(nums[i] == candidate){
     
                cnt ++;
            }
            else{
     
                if(cnt){
     
                    cnt --;
                }
                else{
     
                    cnt = 1;
                    candidate = nums[i];
                }
            }
        }
        return candidate;
    }
};

这串代码的意义在于没意义，单纯的翻译详细实现步骤， 那究竟如何理解呢？
首先，每一个投票人都会把票投给自己！！！
我们初始化候选人是数组的第一个人啦。那么显然地当目前的候选人就是投票人本身时，投票人会给自己投一票确保自己选举上啊。那么假如不符合此上情况呢？？
我想了一个词-----“此消彼长”！！别人要投票给自己的哈，那么不就是等价于自己下降了一票。好吧，更科学一点地说：多了一个投票人也就是总票数多了一票，但这票却不给此候选人，那么此候选人不就在“超半数票”这条路上走远了吗？最后当当前候选人的cnt值为0，也就是但前候选人得票数刚好占总得票数一半时，一旦又有一个投票人不投给他那么其就得下台进行换届选举。
这时会产生一个小疑惑，换届选举可以理解，为啥最后那个投票人直接被选为候选人了呢？
举了个 7 7 7 3 3 3 23的例子，到23的时候刚好进行了换届选举，且23直接当选为候选人，且得票数记为1。这时会产生疑惑，凭啥23就一个人明明是最小几率当选的人偏偏要选他做候选人，而且如果数组就这样结束23不就直接当选上了？
注意看清题，当选人需要获得半数以上的票，我们默认给到的测试数据都是成立的，那么显然上述情况并不存在发生的可能。
换上23当选为啥无所谓？因为只要3够多或者7够多到时候还会拉回来的啦。具体怎么证明有点困难，就不详述了。
仔细看一眼cnt的意义吧，cnt实际上就是当前候选人获得的票数与未获得票数（总票数-自己获得的票数）的差值。
当cnt为0时，当前候选人已经完全没优势了。但为啥不换届？因为其他候选人也没优势啊，顶多也是一半的票数嘛，不满足条件的嘛！！直到cnt为0但下一票仍不给此候选人才进行换届，直接换成下一个人即可。
借用官方题解的神评来说吧：
当遍历到选举人p时，如果此时的候选人不是p，那么p会连同其他候选人一起不投给此候选人。（如果某个时刻cnt为0了，那么此选举人p的一票会直接导致换届，当前候选人换届。）
当p本身就是候选人时，p定然会投给自己。
((n + 1) / (m + 1)) > (n / m)啊，所以原来超过半数现在更棒了！继续当选！
好了，那么绿色的难度是不是太easy了呢。变黄！！

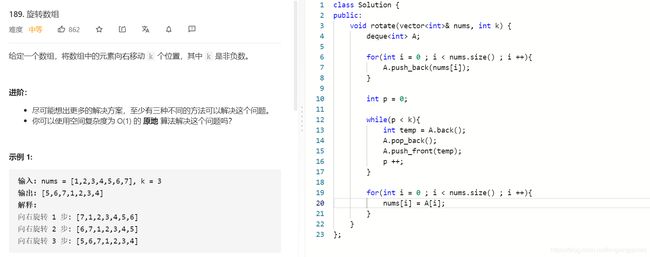
讲道理这道题WA了3次，最后还算是对了。
我一开始是把从后往前k个需要移动的元素进行取值并保存。然后再把剩下的 nums.size() - k 个元素往后挪k个单位，最后再把刚刚保存下来的数放到数组的开头。
感觉没啥不对啊（doge）
很好，测试数据重拳出击，第一组就WA了。
那数据长啥样呢？ “ [1], 2 ”。
是啥，这样怎么从前往后取2个元素呢？显然，一开始的我并不死心，我加了一条语句。

if(nums.size() != 1){
     
	... // 就是刚刚陈述的步骤
}

感觉又行了呢
紧接着，WA了一组数据是 “[-1, -2, 100, 99], 5”。这样一来才令本菜鸡“痛改前非”。
加一个判断nums.size() < k 时的比较，还是另寻他法？
猛然间想着当k极大，前面数组比较少时用我的方法分析简直要自闭 。
试想如果数据为“[1, 2，3, 4，5, 6，7]， 100”,我岂不是得先算出整循环了几次（等效于无效作用），用那个余数（实际起作用部分）来算。
不喜欢！
于是先想到了队列，但队列是先进先出的对于此题操作有局限性（需要尾部弹出元素头部压入此元素），别慌，还有双端队列 deque！
队列详解会在下下次，即链表之后复习到，这里仅说一下思想。
首先把数组里的元素全部压入队列A中。
然后每一次操作都是把现在在队列尾端的那个数弹出后放置到队列的最前端。
最后再把队列最后的顺序重新返还给数组nums即可。
so easy，也挺高效的。

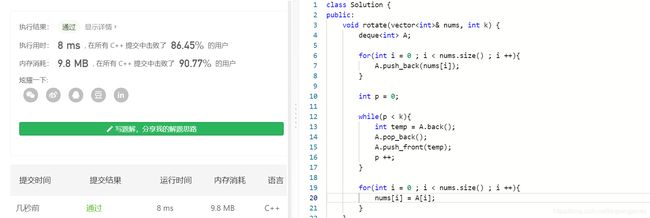
当然啦，数学灵性好的银可能一眼就看出了规律，详情：
利用数学规律解题（方法二）
变红！！
仔细研究了一下，困难题还是涉及到的技巧性和一些算法导论的知识比较多。想着讲完链表后（也就是复习完一轮指针后）再来补上。