人工智能导论笔记-第二章-知识表示

一阶逻辑谓词知识表示：

    命题：

        定义：一个非真即假的陈述句

        一个命题可在一种条件下为真，在另一种条件下为假(例：1+1=10)

        命题逻辑：研究命题及命题之间关系的符合逻辑系统(P：北京是中国的首都)

        命题逻辑表示法：无法把它所描述的事物的结构及逻辑特征反映出来，也不能把不同事物间的共同特征表述出来(P：老李是小李的父亲)

    谓词：

        谓词的一般形式：P(x1,x2,......,xn)

        个体x1,x2,......,xn：某个独立存在的事物或某个抽象的概念

        谓词名P：刻画个体的性质、状态或个体间关系

        个体是常量：一个或一组指定的个体

            例：

                老张是一个教师：TEACHER(Zhang)

                5>3：GREATER(5)

        个体是变元：没有指定的一个或一组个体，只有把个体赋值后才能判断真假

            例：

                x<5：LESS(x,5)

        个体是函数：一个个体到另一个个体的映射

            例：小李的父亲是教师：TEACHER(FATHER(Li))

        个体是谓词

    谓词公式：

        连接词：

            否定：非

            析取：或，∨

            合取：与，∧

            蕴含：如果..那么，->

            等价：当且仅当，<->

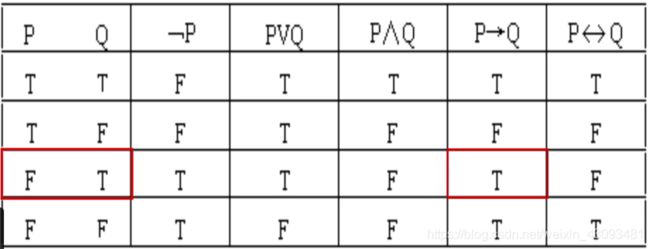
        谓词逻辑真值表：

            

        连接词的优先级：量词、非、合取、析取、蕴含、等价

        量词：

            全称量词( ∀x)：对个体域中所有个体x

                例：所有机器人都是灰色的：(Vx)[ROBOT(x)]->COLOR(x,GRAY)]

            存在量词( ∃x)：在个体域中存在个体x

                例：1号房间有个物体：（ ∃x）INROOM(x,R1)

            全称量词和存在量词：出现的次序会影响命题的意思

                (∀x)(∃y)F(x,y)：表示对于个体域中的全部个体x都存在一个个体y，x与y是朋友

                (∃x)(∀y)F(x,y)：表示在个体域中存在个体x，与个体域中的任何个体y都是朋友

                (∃x)(∃y)F(x,y)：表示在个体域中存在个体x与个体y，x与y是朋友

                (∀x)(∀y)F(x,y)：表示对于个体域中的任何两个个体x和y，x与y都是朋友

            量词的辖域：位于量词后面的单个谓词或用括号括起来的谓词公式

            约束变元与自由变元：辖域内与量词中同名的变元称为约束变元；不同名的变元称为自由变元

                例：(∃x)(P(x,y) - > Q(x,y)) ∨ R(x,y)

                       (P(x,y) - > Q(x,y))：(∃x)的辖域，辖域内的变元x是受(∃x)约束的约束变元，R(x,y)中的x是自由变元，所有y都是自由变元

        谓词公式：

            原子谓词公式：单个谓词是谓词公式

            谓词公式：对谓词进行自由包含和组合连接词与量词所构成的公式

        谓词公式的解释：

            谓词公式在个体域上的解释：个体域中的实体对谓词演算表达式的每个常量、变量、谓词和函数符号的指派

            对于每一个解释，谓词公式都能求出一个真值

        谓词公式的性质：

            永真性：如果谓词公式P对个体域D上的任何一个解释都取得真值T，则成P在D上是永真的；如果P在每个非空个体域上均永真，则P永真

            可满足性：对于谓词公式P，如果至少存在一个解释使得P在此解释下的真值为T，则称P是可满足的，否则，则称P是不可满足的

            等价性：设P与Q是两个谓词公式，D是它们共同的个体域，若对D上的任何一个解释，P与Q都有相同的真值，则称公式P和Q在D上是等价的，若D是任意个体域，则称P和Q是等价的，记为P<=>Q

            谓词公式的永真蕴含：对于谓词公式P与Q，如果P->Q永真，则称公式P永真蕴含Q，且称Q为P的逻辑结论，称P为Q的前提，记为P=>Q

        推理规则：

            三段论：P，P->Q =>Q

            反证法：P=>Q，当且仅当P∧^Q <=>F，即Q为P的逻辑结论，当且仅当P∧^Q是不可满足的

 

    谓词公式表示知识的步骤：

        定义谓词及个体

        变元赋值

        用连接词连接各个谓词，形成谓词公式

 

    一阶谓词逻辑表示法的特点：

        优点：自然性、精确性、严密性、容易实现

        局限性：不能表示不确定的知识、组合爆炸、效率低

        

产生式表示法：

    各种情况的表示：

        确定性规则的表示：

            基本形式：IF P THEN Q 或P->Q

        不确定规则的表示：

            基本形式：IF P THEN Q (置信度) 或 P->Q (置信度)

        确定性事实的表示：

            三元组表示：(对象，属性，值) 或 (关系，对象1，对象2)

        不确定性事实的表示：

            四元组表示：(对象，属性，值，置信度) 或 (关系，对象1，对象2，置信度)

    产生式与谓词逻辑中蕴含式的区别：

        表示范围不一样：除逻辑蕴含外，产生式还包括各种操作、规则、变换、算子、函数等

        蕴含式只能表示精确的知识，而产生式不仅能表示精确的知识，还可以表示不精确的知识

    产生式的形式描述及语义--巴克斯范式：

        符号含义：

            “::=” 表示“定义为”

            “|”    表示“或者是”

              "[]"     表示“可缺省”

        表示：

            <产生式>::=<前提>-><结论>

            <前提>::=<简单条件>|<复合条件>

            <复合条件>::=<简单条件>AND<简单条件>[AND<简单条件>...|<简单条件>OR<简单条件>[OR<简单条件>...]]

            <操作>::=<操作名>[(<变元>,...)]

 

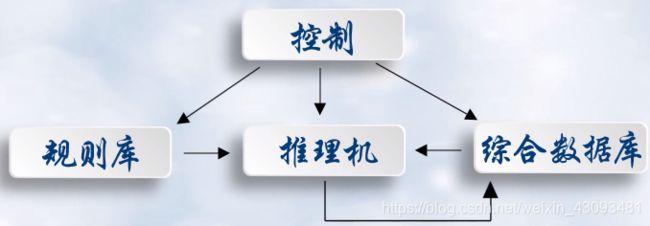
    产生式系统：

        

        规则库：用于描述相应领域内知识的产生式集合；运行时不变

        综合数据库：用于存放问题求解过程中各种当前信息的数据库；运行时不断改变

        控制系统：

            从规则库中选择与综合数据库中的已知事实进行匹配

            匹配成功的规则可能不止一条，进行冲突消解

            执行某一规则时，如果其右部是一个或多个结论，则把这些结论加入到综合数据库中；如果其右部是一个或多个操作，则执行这些操作

            对于不确定性知识，在执行每一条规则时还要按一定的算法计算结论的不确定性

            检查综合数据库中是否包含了最终结论，决定是否停止系统的运行

 

    产生式系统的特点：

        优点：自然性、模块性、有效性、清晰性

        缺点：效率不高、不能表达结构性知识

        适合产生式表示的知识：

            领域知识间关系不密切，不存在结构关系

            经验性及不确定性知识，且相关领域中对这些知识没有严格、统一的理论

            领域问题的求解过程可被表示为一系列相对独立的操作，且每个操作可被表示为一条或多条产生式规则

 

语义网表示法

    概述：是一种采用网络形式表示人类知识的方法。一个语义网络是一个带标识的有向图，其中，带标识的结点标识问题领域中的物体、概念、事件、动作或态势

    基本命题的表示：

        以个体为中心组织知识的语义联系：

            实例联系：用于表示类结点与所属实例结点之间的联系，通常标识为ISA

                例：

            泛化联系：用于表示一种类结点(如鸟)与更抽象的类结点(如动物)之间的关系，通常用AKO表示

                例：

            其他关系：

                <——subject —— 动词 —— object——>

                subject 该动词执行所属的事物，object表示该动词的对象

                例：鸽子<-subject-|拥有|-object->翅膀

            聚集联系：用于表示某一个体与其组成成分之间的联系，通常用Part-of表示

                例：

            属性联系：用于表示个体、属性及其取值之间的联系，通常用有向弧表示属性，用这些弧指向的结点表示各自的值

                例：

        连接词的表示方法：

            

            通过修改其中内容，可表示：与、或、非、蕴含

        变元和量词的表示：

            存在量词：直接用ISA弧表示

            全称量词：用分块方法表示

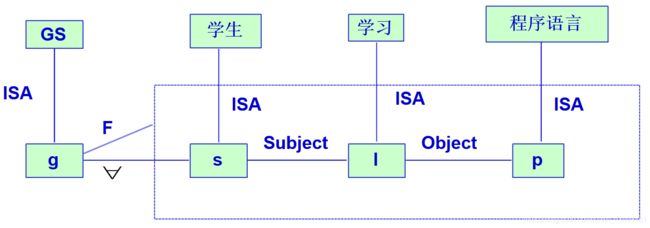
                例：每个学生都学习了一门程序设计语言

                

                    GS：概念结点，表示具有全称量化的一般事件

                    g：实例结点，代表GS中的一个具体例子

                    s：全称变量，表示任一(全部)学生

                    I：存在变量，表示某一次学习

                    P：存在变量，表示某一门程序设计语言

                    弧ISA：表示g是GS中的一个实例

                    弧F：说明它所代表的子空间及其具体形式

                    弧∀：说明它所代表的全称量词

    

 

框架表示法

    框架：一种描述所论对象属性的数据结构

        一个框架由若干个槽构成，每个槽又可根据实际情况划分为若干个侧面

        一个槽用于描述所论对象的某一方面的属性

        一个侧面用于描述相应属性的一个方面

        槽和侧面所具有的属性值分别被称为槽值和侧面值

    表示：

        

 

    特点：

        结构性、继承性、自然性