平衡小车从原理到实践
平衡小车从原理到实践
作者:公众号:小白学移动机器人
关于内容:参考很多网上大佬的博客加上自己的理解而成,适合平衡车初学者和想要了解原理的小伙伴。
1、平衡小车控制原理
先记住一句话,直立环和速度环的结合是保持小车长期稳定平衡的前提。相信大家读到最后一定可以明白这句话的含义。
举个例子
大家都玩过的用手控制木棍直立不倒的游戏。这是一个通过眼睛观察木棒的倾角和倾斜趋势(角速度),通过手指的移动去抵消木棒倾斜的角度和倾斜的趋势使木棒能直立不倒的一个过程。典型的负反馈机制。
平衡小车也是如此,小车运动方向与倾斜方向一致,通过测量小车的倾角和倾角速度,进而通过控制小车车轮的加速度来消除小车的倾角和倾角速度,这样理论上不考虑电机极限的情况下,小车就可以平衡。
直立环的引出
理想情况下,控制电机的加速度和小车倾角成正比,可以让小车保持平衡,就是小车向倾斜的方向运动,倾斜角度越大,小车运动越快。
a = k p ∗ θ a=kp*θ a=kp∗θ
但实际上,小车刚体绕轴旋转时具有惯性,当小车到达倾角为零时,a输出零,因为惯性的存在,小车还是会向另一个方向倒去。如此反复,小车将一直振荡无法静止。
如何消除小车绕轴转动的惯性,也就是消除小车的转动惯量,使小车尽可能的静止呢?
首先分析转动惯量,公式如下:
I = ∑ i m i r i 2 I=\sum_{i}m_i{r_i}^2 I=i∑miri2
其中m是质量,r是质点到转轴的垂直距离,m和r都无法为零,所以转动惯量客观存在。
既然不能使转动惯量为零,换个角度,是不是可以抵消转动惯量呢?
这里分析一下单摆模型吧。
由于重力的作用,单摆受到和单摆角度成正比与运动方向相反的回复力;类比电机的加速度
由于空气的作用,单摆又受到和单摆运动速度成正比与运动反向相反的阻尼力,使单摆最终平衡下来。
有没有启发,为了让小车能近似静止,还需要一个阻尼力,这个阻尼力和小车的倾角速度成正比。
所以,小车的平衡控制算法改写为:
a = k p ∗ θ + k d ∗ θ ⋅ a=kp*θ+kd*θ^· a=kp∗θ+kd∗θ⋅
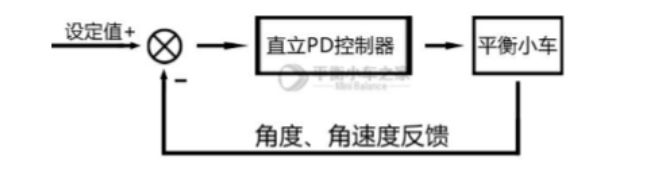
一个是角度偏差,另一个是角度偏差的变化率,也就是角速度。为了简化控制,a的输出直接作为直流减速电机的PWM替代。这里引入PID,关于PID的理论就不讲了,网上大佬巨多。上面的公式就是一个位置式离散PD控制器。负反馈机制。
关于直立PD控制器的参数整定,也就公式中角度和角速度的参数整定,这里根据公式原理也可以得到一些调试技巧。
比例控制:回复力
微分控制:阻尼力抵消转动惯量
微分系数与转动惯量有关,根据转动惯量和力矩的公式:
I = ∑ i m i r i 2 I=\sum_{i}m_i{r_i}^2 I=i∑miri2
M = ∑ i F i L i M=\sum_iF_iL_i M=i∑FiLi
小车质量M固定的情况下,重心越高(r、L越大),需要的回复力F越小,所以比例系数kp变小;转动惯量I变大,所以微分系数kd变大。
小车重心(r、L)固定的情况下,质量M增大,需要回复力增大,所以比例系数kp增大;转动惯量I变大,所以微分系数kd变大。
速度环的引出
往往,我们只使用直立环,小车只能短暂的平衡几秒,然后就朝着一个方向倒去了。
具体原因要从具体的平衡控制结构来分析。我们使用的传感器是单一的MPU6050,通过DMP库获取数据,输出的是角度以及角速度信号,而我们控制的是电机,不考虑电机的感受(也就是电机的速度幅值),只要求平衡车的角度能够保持绝对平衡。
只有直立环的平衡小车会倒下的原因:
那么假如小车现在平衡状态,控制闭环出现了微小的干扰,平衡车就会有一个方向的加速度,而此时小车角度平衡,小车平移速度没有限制,这样就可能超过PWM的幅值,导致电机无法加速了,也就没有了有效的回复力,所以小车就倒了。
所以速度环出现了,在小车平衡的同时,尽量让小车保持静止,就是小车速度为零。也就是对小车平移速度进行限制。
平衡小车速度环的原理:
根据经验知道,小车的运行速度和小车的倾角是相关的,比如小车前倾,是不是直立环要使小车向前加速,让小车保持平衡,此时小车不就有速度了嘛。如果对着速度进行闭环控制,那么这个环不就是速度环了嘛。如果将速度环的目标设置为0,小车不就可以长期稳定平衡了嘛。
大家之前了解的电机速度PID基本上都是负反馈,但是在以直立为主的平衡车系统中,负反馈的速度控制将会导致小车加速到下。这里我们通过让小车保持一定的角度,用小车平衡的过程,表示速度闭环的控制。我们可以通过串级PID的方式,如下图所示:
根据上面的原理图,我们把速度和直立两个控制器串联起来,速度环的输出作为直立环的输入,直立环的输出就是系统的输出,这样就可以保持平衡。
公式如下:
a 1 = k p 1 ∗ e ( k ) + k i 1 ∗ ∑ e ( k ) a_1=kp_1*e(k)+ki_1*\sum{e(k)} a1=kp1∗e(k)+ki1∗∑e(k)
a = k p ∗ ( θ − a 1 ) + k d ∗ θ ⋅ a=kp*(θ-a_1)+kd*θ^· a=kp∗(θ−a1)+kd∗θ⋅
这样把速度控制系统输出看做是一个角度,原本要保持角度为零就变成保持一个小的角度a1,也就是上面说过的平衡小车速度环的原理。
所以我们就有了一个这样的算法,两个式子合并。
a = k p ∗ θ + k d ∗ θ ⋅ − k p [ k p 1 ∗ e ( k ) + k i 1 ∗ ∑ e ( k ) ] a=kp*θ+kd*θ^·-kp[kp_1*e(k)+ki_1*\sum{e(k)}] a=kp∗θ+kd∗θ⋅−kp[kp1∗e(k)+ki1∗∑e(k)]
进行转化演变:
将上面的算法,转化成为:一个单独的负反馈的直立环 + 一个单独的正反馈的速度环,也就是大家常说的平衡车的速度环是正反馈的由来。
2、制作一个平衡小车
如果大家看完上面的内容已经跃跃欲试了,下面的图帮你整理了制作一个平衡小车需要准备什么硬件?需要完成具体的任务?软件实现步骤?
关于初级玩具平衡小车的主控部分的电路模块有以下参考,图片来源淘宝。
如果对硬件不是很感冒的同学,完全可以购买配件组装,或者买个成品车,重在学习控制算法嘛。
3、平衡小车-PD直立环
假如现在你已经拥有一辆平衡小车了,在完成电机的PWM控制、编码器测速、MPU6050数据读取之后,我们就开始了平衡小车PD直立环的设计。如果没完成可以看我之前的文章。
之前的文章链接
电机的PWM控制:
电机编码器测速:
MPU6050数据读取:
单独PD直立环最终效果:使小车能够稳定一小段时间。原因上面讲过,电机速度存在极限。
PD直立环的代码:
/**************************************************************************
函数功能:直立环PD控制
入口参数:角度、角速度
返回 值:直立控制PWM
**************************************************************************/
int balance(float Angle,float Gyro)//roll(横滚角)(回复力)、角速度(阻尼力)
{
float Bias;
float Balance_Kp=700,Balance_Kd=2.0;//600 kp(0 - 720) kd( 0 - 2 )
// float Balance_Kp=0,Balance_Kd=0; //===调试用
int balance;
Bias=Angle-ZHONGZHI; //===求出平衡的角度中值 和机械相关
balance=Balance_Kp*Bias+Gyro*Balance_Kd; //===计算平衡控制的电机PWM PD控制 kp是P系数 kd是D系数
return balance;
}
PD直立环参数:
Kp增加回复力的响应速度
Kp过小,响应太慢,不能达到直立。
Kp过大,会出现大幅度低频振荡。
Kd消除Kp过大带来的低频振荡。
Kd过大,会出现高频抖动。
入口参数:
int balance(float Angle,float Gyro)
如果小车是绕MPU6050的x轴旋转,Angle是roll值(横滚角), Gyro是对应的角速度
如果小车是绕MPU6050的y轴旋转,Angle是pitch值(横滚角),Gyro是对应的角速度
机械中值:
需要调整,每辆车因为机械原因,可能都不一样
机械中值也就是代码中参数ZHONGZHI,这个值根据自己MPU6050的安装位置而定。
如果小车是绕MPU6050的x轴旋转,ZHONGZHI是前倾和后仰临界点的roll值(横滚角)
如果小车是绕MPU6050的y轴旋转,ZHONGZHI是前倾和后仰临界点的pitch值(俯仰角)
直立环的Kp范围确定:
如果你的电机PWM=7200为满幅,即占空比100%。
如果kp=720,角度偏差10度,电机就到达满转了。我们不会容忍小车偏差10度以上,所以kp的范围(0 - 720),但是具体情况具体分析。
直立环的kp极性确定:
这个和自己的PWM设定方向、角度方向有关,但是我们可以不考虑这些。
我们直接看现象,如果设定kp=-500,小车加速倒下,那么kp的极性为负,当kp=500的时候,可以尽可能维持平衡。
直立环的kp大小确定:
首先,将直立环kd和速度环、转向环的参数设置为0。
然后,试凑法+二分法,从小到大调到小车出现大幅度低频振动,确定kp。不用纠结参数调试,有一个感觉好的就用,找到最好的很不容易,浪费时间。
直立环的kd极性确定:
这个和自己的PWM设定方向、角速度方向有关,但是我们可以不考虑这些。
我们直接看现象,如果设定kp=0,设置kd=-2,小车加速倒下,那么kd的极性为负,当kd=2的时候,可以尽可能维持平衡。
直立环的kd大小确定:
在之前直立kp的基础上,试凑法+二分法,从小到大调试kd大小,一直到小车出现高频的剧烈抖动。
根据工程经验,将直立环的kp和kd同时乘以0.6,就是我们最终要的直立环的参数。
4、平衡小车-PI速度环
PD直立环+PI速度环的效果:使小车长期的平衡下来。
终极效果:几乎静止不动,但是没必要花时间调试,重在学习理论和实践过程。
根据上面的控制理论,我们将小车的控制系统划分为负反馈的PD直立环+正反馈的PI速度环。
平衡小车,顾名思义平衡为主,其他为辅,为了让直立环处于主导地位,对速度环进行适当的低通滤波处理,也就是上面理论部分的公式,对速度环的kp处理。
PI速度环的代码:
/**************************************************************************
函数功能:速度环PI控制 修改前进后退速度
入口参数:左轮编码器、右轮编码器
返回 值:速度控制PWM
**************************************************************************/
int velocity(int encoder_left,int encoder_right)
{
static float Velocity=0,Encoder_Least=0,Encoder=0,Movement=0;
static float Encoder_Integral=0;
float Velocity_Kp=-180,Velocity_Ki=Velocity_Kp/200.0;//-185 -0.925
// float Velocity_Kp=0, Velocity_Ki=Velocity_Kp/200.0; //===调试用
//=============速度PI控制器=======================//
Encoder_Least =(encoder_left + encoder_right)-0; //===获取最新速度偏差==测量速度(左右编码器之和)-目标速度(此处为零)
Encoder *= 0.8; //===一阶低通滤波器
Encoder += Encoder_Least*0.2; //===一阶低通滤波器
Encoder_Integral +=Encoder; //===积分出位移 积分时间:5ms
Encoder_Integral=Encoder_Integral-Movement; //===接收遥控器数据,控制前进后退
if(Encoder_Integral>10000) Encoder_Integral=10000; //===积分限幅
if(Encoder_Integral<-10000) Encoder_Integral=-10000; //===积分限幅
Velocity = Encoder*Velocity_Kp+Encoder_Integral*Velocity_Ki; //===速度控制
return Velocity;
}
入口参数:
int velocity(int encoder_left,int encoder_right)
首先,encoder_left、encoder_right代表的是左右电机速度量的意义。
实际上,encoder_left、encoder_right为单位时间内(比如5ms),左右电机编码器分别的变化量,通过定时器编码器模式采集,可正可负。
Encoder_Least =(encoder_left + encoder_right)-0;
上面一句代码是算法中求速度偏差的,有些同学不理解为什么是encoder_left + encoder_right表示当前小车速度。关于小车速度有这样一个公式
s p e e d = ( l e f t S p e e d + r i g h t S p e e d ) / 2 speed=(leftSpeed+rightSpeed)/2 speed=(leftSpeed+rightSpeed)/2
这里只是没有除以2而已,仔细想想,有必要除以2吗?当然是没有必要,我们调试的最终参数是参与量化的。
速度环的Kp范围确定:
通过实验测得,小车满速时,单位时间内(5ms)小车的左右编码器变化之和可达100,(不同的电机可能不一样),假定速度偏差达到50%电机满转。
100/2=50,7200/50=144,也就是kp最大144,但是这里假设速度偏差达到50%电机满转的情况,所以具体情况具体分析。
速度环的Kp极性确定:
正反馈的效果,是把情况变得更剧烈。
这里先关闭直立环和转向环,设置kp=-80,用手转动一侧电机,如果两个电机开始向相同的方向加速,即为正反馈过程,若不是kp为正值。
速度环的kp大小确定:
首先,打开之前调好的直立环。
试凑法+二分法,从小到大调整kp,(公式中提到ki=kp/200),直到使得小车的响应迅速又稳定,此时,平衡小车的第一部分就调试结束了,小车可以长期稳定的直立了。
5、总结
到这里,极简版的直立平衡小车的理论和实践部分就结束了,个人感觉,这篇文章不像其他的文章只介绍如何实现一个平衡小车。这里从始至终都在向大家传达直立环、速度环的原理、内在机制,这样就可以更好的了解一个系统。
关于为什么将平衡小车代码缩减到最少,这里只留下了直立环和速度环,主要是便于理解和学习。
关于极简版工程代码,在公众号,发送:平衡小车极简版,即可获得。
关于遥控、转向环,下面会陆续发布,尽请期待。
如果你感觉,我的文章比较适合你,关注我,给你不一样的惊喜。
![]()
![]()