【论文学习】ICLR2021，鲁棒早期学习法：抑制记忆噪声标签ROBUST EARLY-LEARNING: HINDERING THE MEMORIZATION OF NOISY LABELS

论文来自ICLR2021，作者是悉尼大学的Xiaobo Xia博士。论文基于早停和彩票假说，提出了一种处理标签噪声问题的新方法。我就论文要点学习整理，给出我的代码实现，对论文中部分试验复现，并补充进行一些新试验。
论文链接
作者承诺代码开源，但目前暂未开源。

---

一、理论要点

  这篇文章基于两点主要理论：一是深度网络会先记忆标签清晰的训练数据，然后记忆标签有噪声的训练数据。因此，用早停法学习可抑制噪声标签。二是彩票假说指出深度网络中只有部分参数对模型起作用，本文因此认为只有部分参数对拟合干净标签有用，称之为关键参数，而其他参数则倾向于拟合噪声标签，称之为非关键参数。在每次迭代中，对不同的参数执行不同的更新规则以逐渐使非关键参数归零，以此抑制噪声标签发挥作用。

二、公式推导

文中总共有以下6个公式：
min $L(\mathcal{W};S)$ = min$\frac{1}{n}\sum _{i=1}^{n}L(\mathcal{W};(x_i,y_i))+\lambda {\Vert \begin{array}{c}\mathcal{W}\end{array}\Vert }_1$        (1)

$\mathcal{W}(k+1)\leftarrow \mathcal{W}(k)-\eta (\frac{\partial L(\mathcal{W}(k);S^{\ast })}{\partial \mathcal{W}(k)}+\lambda sgn(\mathcal{W}(k)))$      (2)

$g_i=|\nabla L(W_i;S)\times W_i|,i\in [m]$                 (3)

$m_c=(1-\tau )m$                         (4)

${\mathcal{W}}_c(k+1)\leftarrow {\mathcal{W}}_c(k)-\eta ((1-\tau )\frac{\partial L({\mathcal{W}}_c(k);\widetilde{S^{\ast }})}{\partial {\mathcal{W}}_c(k)}+\lambda sgn({\mathcal{W}}_c(k)))$ (5)

${\mathcal{W}}_n(k+1)\leftarrow {\mathcal{W}}_n(k)-\eta \lambda sgn({\mathcal{W}}_n(k))$             (6)

考虑给损失函数加入一个l1正则项，如式（1）；
根据式（1）的损失函数，使用SGD方式更新权重，如式（2）；
对于任一个参数$W_i\in {\mathcal{W}}^m$，根据式（3）计算一个参考量$g_i$，根据$g_i$对$\mathcal{W}$排序。根据式（4）计算得到关键参数的个数为$m_c$个，然后$\mathcal{W}$排序考前的$m_c$个参数就是关键参数${\mathcal{W}}_c$，其余参数为非关键参数${\mathcal{W}}_n$;
对于关键参数按照（5）式更新，注意梯度乘上了一个衰减系数（$1-\tau$），作者说这是为了防止训练过程中过度自信下降。（对此不是很理解）
对于非关键参数按照（6）式更新，此时把梯度置零，只保留了正则化项，这会导致这些非关键参数逐渐缩小直到接近于0而失去作用。

其中公式（3）比较难理解，为什么用这个指标来判断哪些是关键参数呢？原文的解释如下：
构造一个函数$G(t)=L(t\mathcal{W};S)$，则
$G^{\prime }(t)=\nabla L(t\mathcal{W};S{)}^T\mathcal{W}$，
令$t=1$，有：
$G^{\prime }(1)=\nabla L(\mathcal{W};S{)}^T\mathcal{W}=<\nabla L(\mathcal{W};S),\mathcal{W}>$（<>表示内积）
满足最优化条件时，$\nabla L(\mathcal{W};S)=0$，因此$G^{\prime }(1)=0$，
由$G^{\prime }(1)=0$可得到（3）式
说实话，这个部分我没有看懂，有理解的小伙伴可以讲一讲。

三、效果对比

  作者指出由于本文的主要目的是提出一个新的概念，并且本文没有使用多种综合措施，所以效果赶不上该领域在2020年的两个SOTA方法：DivideMix和SELF，除了这两个之外，本文方法比其他模型的效果都好。作者进行了大量对比试验，其中在MNIST、F-MNIST、CIFAR-10、CIFAR-100这四个数据集上的试验如表1。

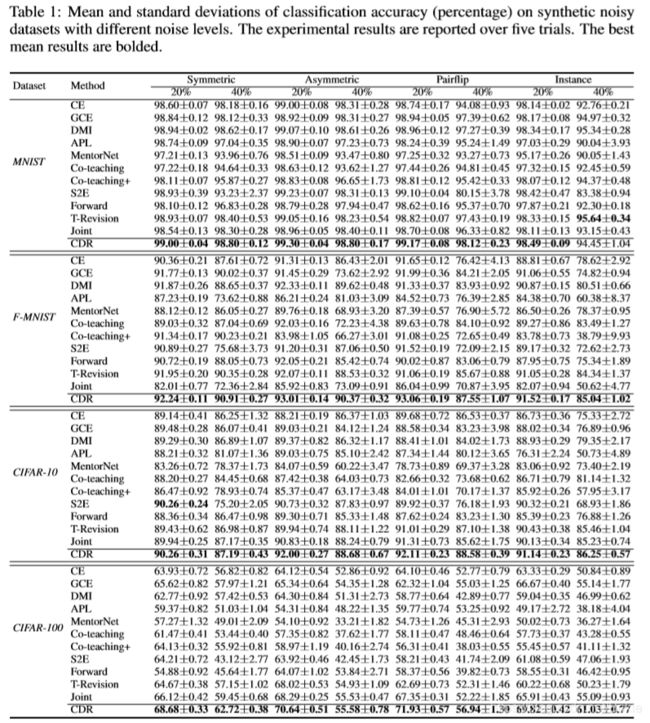
  作者随后又在Food-101和WebVision这两个数据集上进行了试验，结论类似。
  作者又进行了消融试验，试验发现模型效果对参数$\tau$不敏感。

四、我的代码及部分试验复现

1，核心代码

  由于没有开源，我按照自己理解进行代码实现。根据文中公式，该算法只涉及到参数更新过程，因此只需要在pytorch中重写SGD即可实现本算法中说的关键/非关键参数分别更新；然后在训练的时候加入早停即可。
  重写的newSGD代码如下，主要是增加了tau和decay1两个参数。tau就是文中$\tau$噪声率，注意式（6）和式（5）的区别，对于非关键参数，就是把梯度项置零，只有正则化项了，所以代码可以非常简洁的写出来。在SGD中，weight_decay就是正则化项，但是torch1.6给出的SGD用的是l2正则，而论文中给出的公式用的是l1正则，所以我又新加了一个weight_decay1用来实现l1正则。

import torch
from torch.optim.optimizer import Optimizer, required

class newSGD(Optimizer):

    def __init__(self, params, lr=required, momentum=0, dampening=0, weight_decay1=0, tau=0,
                 weight_decay=0, nesterov=False):
        if lr is not required and lr < 0.0:
            raise ValueError("Invalid learning rate: {}".format(lr))
        if momentum < 0.0:
            raise ValueError("Invalid momentum value: {}".format(momentum))
        if weight_decay < 0.0:
            raise ValueError("Invalid weight_decay value: {}".format(weight_decay))

        defaults = dict(lr=lr, momentum=momentum, dampening=dampening,
                        weight_decay=weight_decay, weight_decay1=weight_decay1,
                        tau = tau, nesterov=nesterov)
        if nesterov and (momentum <= 0 or dampening != 0):
            raise ValueError("Nesterov momentum requires a momentum and zero dampening")
        super(newSGD, self).__init__(params, defaults)

    def __setstate__(self, state):
        super(newSGD, self).__setstate__(state)
        for group in self.param_groups:
            group.setdefault('nesterov', False)

    @torch.no_grad()
    def step(self, closure=None):

        loss = None
        if closure is not None:
            with torch.enable_grad():
                loss = closure()

        for group in self.param_groups:
            weight_decay = group['weight_decay']
            momentum = group['momentum']
            dampening = group['dampening']
            nesterov = group['nesterov']
            tau = group['tau']
            weight_decay1 = group['weight_decay1']

            for p in group['params']:
                if p.grad is None:
                    continue
                d_p = p.grad
                
                if tau != 0:
                    g = (d_p * p).abs()
                    m = p.numel()
                    mn = int(m*tau)  
                    if mn>0:
                        kth,_ = g.flatten().kthvalue(mn)
                        d_p = torch.where(g < kth, torch.zeros_like(d_p), d_p)
                    d_p.mul_(1 - tau)
                if weight_decay != 0:
                    d_p = d_p.add(p, alpha=weight_decay)
                elif weight_decay1 != 0:
                    d_p = d_p.add(torch.sign(p), alpha=weight_decay1)
                if momentum != 0:
                    param_state = self.state[p]
                    if 'momentum_buffer' not in param_state:
                        buf = param_state['momentum_buffer'] = torch.clone(d_p).detach()
                    else:
                        buf = param_state['momentum_buffer']
                        buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
                    if nesterov:
                        d_p = d_p.add(buf, alpha=momentum)
                    else:
                        d_p = buf

                p.add_(d_p, alpha=-group['lr'])

        return loss

然后在训练时把原来的SGD替换即可

from newSGD import newSGD
optimizer = newSGD(net.parameters(), lr=0.01,
                   momentum=0.9, tau=0.2, weight_decay1=1e-3)

2，我的试验

  为了加快速度，试验主要在MNIST数据集和LeNet上进行，个别补充进行了CIFAR10上的ResNet18试验。试验参数配置：epoch = 100， BatchSize = 128， lr=0.01 ，momentum = 0.9， weight_decay = 0.001。由于L1正则不便于观察规律（原因见2.4.2节介绍），下面试验使用L2正则。噪声数据只使用同步噪声标签，即每个类别按照噪声率抽取样本随机变换为任意其他类别的标签。注意噪声只存在于训练集，测试集不含噪声，是干净的。

2.1，不同噪声率下观察“早停”的作用

  神经网络在训练早期只学习干净标签，在训练的后期才逐渐学习噪声标签，因此可以用早停法抑制噪声标签。我们先观察这个现象，试验中不使用本文提到的新算法，只使用LeNet和交叉熵损失：

  从图中可以看出几个特点：
（1）随着噪声率的增加，训练集训练精度明显降低，但测试集仍能达到较高的精度，例如即使噪声含量80%时，此时训练集精度不足35%，但测试集精度最高仍可达到85%以上。这说明神经网络本身就对噪声有一定的鲁棒性。
（2）含噪声时，网络早期先学习干净数据，所以测试集仍可以达到很高精度，但后期开始记忆噪声数据，导致测试集精度下降。所以早停肯定可以起到抑制噪声标签的作用。
（3）对比噪声含量80%和90%的训练精度曲线（图中浅蓝和深蓝虚线），我们发现一个有意思的地方，90%噪声的训练精度后期比80%的还高。我的解释是：由于数据集就10个类别，90%噪声时几乎等于完全随机，网络从一开始就意识到这没有任何规律可以找，干脆就快速发展记忆数据能力了。这很有意思，值得继续思考。

2.2，不同$\tau$参数下观察“彩票假说”现象

  彩票假说指出神经网络只有少部分参数真正发挥作用。上面newSGD算法中给出的$\tau$会使得网络中每个参数张量中都有占比例为$\tau$的参数在经过充分训练后趋于0，因此使用这个代码就可以观察到彩票假说现象。我们使用不含噪声的数据来观察这个现象：

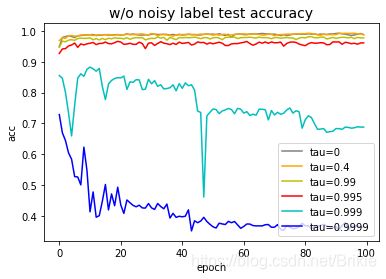
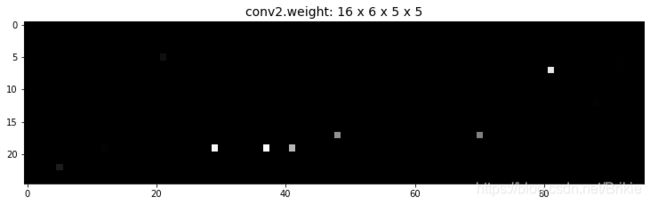
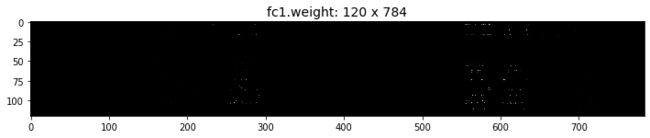
从图中可以看出，神经网络具有惊人的参数压缩潜力，$\tau =0.995$时，相当于只有0.5%的参数起作用，测试精度仍可达到95%以上。$\tau =0.999$时，训练结束后，我们把其中conv2层的权重绝对值reshape到25×96以及fc1层的权重绝对值进行可视化，画出来如下图。可见其中确实只有极少的参数存在了，但即使这么稀疏的参数，仍然可以达到70%以上的精度。$\tau =0.9999$时，网络的效果才有明显的下降，但仍有接近40%的精度。

2.3，不同噪声率和不同$\tau$参数下观察本文算法去噪效果

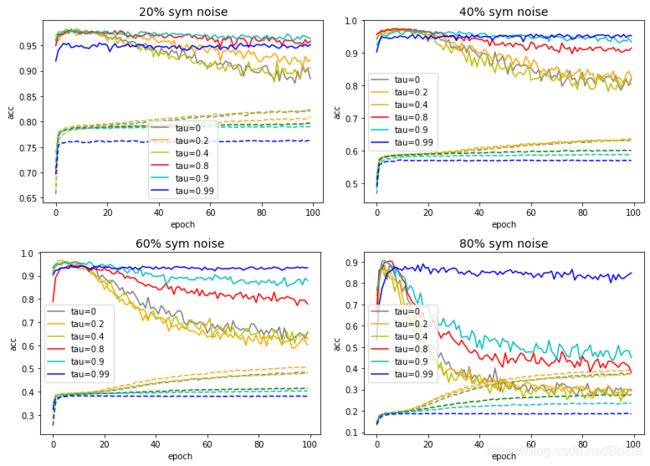
又在CIFAR10上用ResNet18做了部分试验，效果和上图类似：

  从图中可以看出：
  $\tau =0$就是论文Table1中的CE，使用本算法之后，$\tau$较大时起到的作用只是随着训练的继续，测试精度下降变少，但考虑到早停时，最佳精度发生在初期，使用本方法后和CE并无明显优势。这可能是MNIST数据集过于简单，加的噪声模式也比较简单，所以看不出论文算法的优势。这个和论文中的Table1也是一致的。

2.4，算法局部修改试验

  对算法中的衰减系数（$1-\tau$），l1正则，划分关键参数的判据$g_i$等的作用和必要性仍不太理解，因此我们从试验对比中观察它们的效果。

2.4.1 （$1-\tau$）

对于式（5）中的（$1-\tau$）项，在原本的SGD公式中是没有的，作者说这里增加此项能够抑制过度自信下降的作用，下图以20%噪声率为例，对比了使用（$1-\tau$）和不使用（$1-\tau$）的效果。

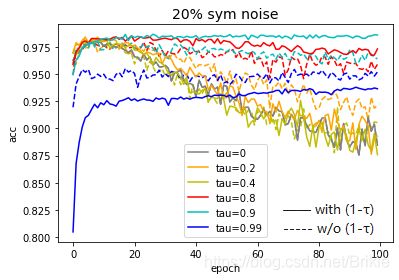
从图中可以看出，当$\tau$=0.8或0.9时，（$1-\tau$）项能够起到一定的正则效果，会避免训练的后期记忆噪声数据，但效果并不明显。

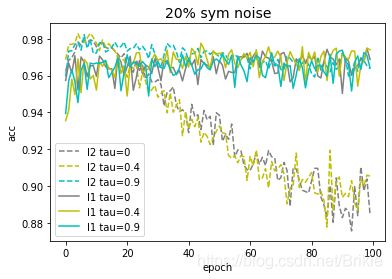
2.4.2 L1正则

下图给出L1正则和L2正则在20%噪声率时的测试集精度曲线，可以看出L1正则的正则化效果更重，即使$\tau$较小时也可以防止模型后期记忆噪声数据。但是L1正则在模型初期的精度表现不如L2正则，也就是说如果使用早停的话其效果不如L2。由于L1正则过强的正则化效果，不便于观察2.1，2.2节中的现象，所以前序试验都使用L2正则进行。

2.4.3 $g_i$

  $g_i$是划分关键和非关键参数的依据，作者在公式（3）中给出的计算方法是参数的梯度和参数的点积的绝对值。作者的推导过程我没有看懂（数学太菜了！），但我可以用试验检验以下这个表达式的充分必要性，也就是

• 使用式（3）能否把参数压缩到少量关键参数；
• 使用式（3）确定的关键参数是否真的关键，即是否能以少量关键参数仍达到和全量参数接近的精度；

  文中公式（3）我在代码中写成 g = (d_p * p).abs()，我又尝试了其他几种划分关键和非关键参数的方法，
  方法B：g = d_p.abs() + p.abs()
  方法C：提前随机选定每个参数张量中占比$\tau$的位置制成mask，然后每轮参数更新时，这些位置对应的参数的梯度置0。

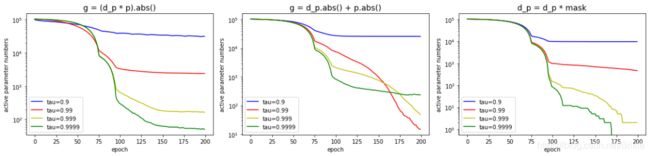
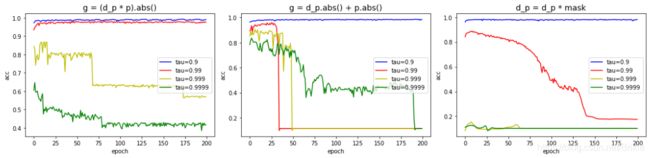
  我们定义绝对值大于0.001的参数为有效参数，上图的第一行三个图表示的是随着训练轮数，网络中的总有效参数量的变化情况，第二行三个图表示随着训练轮数，测试集精度的变化。
  从上面图中对比我们可以看出，对于本文方法（最左图），在不同的$\tau$下都能使有效参数量逐渐收缩到占比总参数量约为$\tau$的位置处，并且精度仍能够有着不错的保持。而对于另外两种方法，它们不能够保持有效参数不再压缩，而是会出现参数量不断的下降，精度也掉的一塌糊涂，说明这两种方法不能有效区分关键参数和非关键参数，也就不能够在训练后期把关键参数稳定住。实际上我还尝试了很多其他的参数划分方法，都没有文中方法有效。
  所以说文中式（3）给出的关键参数划分判据是非常有效的，对公式的推导过程后续再慢慢吃透。
  （补充说明，第一行图中可以明显观察到有效参数量每次都是在75epoch和95epoch处有明显转折，这个原因是网络使用的默认的标准参数初始化方式，参数的分布概率是固定的，而同样的weight_decay下参数的收缩速率也是固定的，所以会有同批的参数被同时收缩到0.001以下。）

五、读后感

  本文提出的方法实际上主要是从彩票假说和神经网络早期学习干净标签这两点出发，本文方法的噪声标签抑制能力实际上达不到SOTA。但彩票假说中只是指出了神经网络中真正关键的参数很少，却也没有指出有效的提取关键参数的方法，而本文提出的划分关键参数的方法非常有意思，有可能提供一种新的模型压缩的思路。这篇论文的写作也非常好，值得学习。

---

<补充 2021-02-09>更具tau修正梯度的核心部分代码修改如下，能够进一步提高精度，加快运算速度。

                m = p.numel()
                if tau != 0 and m>1000:
                    g = (d_p * p).abs()
                    if m>10000:
                        gf = g.flatten()[:10000]
                        mn = int(10000*(1-100/math.sqrt(m)*(1-tau)))
                        if mn > 9990:
                            mn = 9990
                        kth,_ = gf.kthvalue(mn)
                    else:
                        mn = int(p.numel()*tau)
                        kth,_ = g.flatten().kthvalue(mn)
                    d_p = torch.where(g < kth, torch.zeros_like(d_p), d_p)