《动手学深度学习》第四天之softmax回归

首先学习第三章第五节–图像分类数据集
主要解释一下对于函数的定义
（一）定义 get_fashion_mnist_labels(labels) 函数来将数值标签转成相应的文本标签：
将用的到的衣服类别定义在一个数组里面，通过将数组下表和数组内容对应进行转换。
（二）定义 show_fashion_mnist(images, labels) 函数在一行里画出多张图像和对应标签的函数：
①首先调用函数 d2l.use_svg_display() 用矢量图显示，
②然后调用函数 d2l.plt.subplots()
函数原型是

def subplots(nrows=1, ncols=1, sharex=False, sharey=False, squeeze=True,
             subplot_kw=None, gridspec_kw=None, **fig_kw):
    fig = figure(**fig_kw)
    axs = fig.subplots(nrows=nrows, ncols=ncols, sharex=sharex, sharey=sharey,
                       squeeze=squeeze, subplot_kw=subplot_kw,
                       gridspec_kw=gridspec_kw)
    return fig, axs  

那么在此应用时，便是把子图的行数设为1，列数设为图片的个数，并且通过将参数**fig_kw设为figsize = (12,12)使得图片设为长宽均为12的尺寸。
③zip相当于压缩，zip(*)相当于解压。
例如，对于
x=[“a”,“1”]
y=[“b”,“2”]
z = list(zip(x,y))
print (list(zip(x,y)))
print (list(zip(*z)))
结果为：
[(‘a’, ‘b’), (‘1’, ‘2’)]

[(‘a’, ‘1’), (‘b’, ‘2’)]
④通过for循环，将所有的图像的名字和图片相应的显示出来，同时将图片的大小变为（28,28）。
（三）读取小批量
①mxnet.gluon.data.vision.transforms.ToTensor():
将图像数组转换为张量数组。将[0，255]范围内的形状(长×宽×宽)的图像数组转换为[0，1范围内的浮动32张量形状(长×宽×宽)数组。
将图像数据从uint8格式变换成32位浮点数格式，并除以255使得所有像素的数值均在0到1之间。ToTensor实例还将图像通道从最后一维移到最前一维来方便之后介绍的卷积神经网络计算。
②sys.platform该变量返回当前系统的平台标识
当系统是win时，不支持多进程来加速数据读取，所以num_workers=0
③mxnet.gluon.data.DataLoader(dataset, batch_size=None, shuffle=False, sampler=None, last_batch=None, batch_sampler=None, batchify_fn=None, num_workers=0, pin_memory=False, pin_device_id=0, prefetch=None, thread_pool=False)

transform_first（fn）
返回一个新数据集，每个样本的第一个元素由transformer函数fn转换
所以在这个实例中，就是将第一个元素用To Tensor转换了。
训练数据要打乱顺序，测试数据不需要打乱顺序。

接着学习第三章第六节–softmax回归
（一）实现softmax运算：
定义softmax运算，得到的矩阵每行元素和为1且非负。因此，该矩阵每行都是合法的概率分布。softmax运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。
（二）定义模型：
首先通过X.reshape((-1, num_inputs)，将X变成列数为 num_inputs的向量，然后通过nd.dot()实现W和X的向量相乘，然后与b相加，再通过softmax回归运算，实现变成概率。
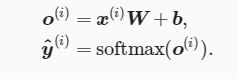（三）定义损失函数：

> mxnet.ndarray.pick(data=None, index=None, axis=_Null, keepdims=_Null,

mode=_Null, out=None, name=None, **kwargs)

根据沿给定轴的输入索引从输入数组中选取元素。给定形状(d0，d1)的输入数组和形状(i0)的索引，结果将是形状(i0)的输出数组，其中:输出[i] =输入[i，索引[i]]

定义cross_entropy(y_hat, y)为交叉熵函数

（四）计算分类准确率：
定义准确率accuracy()函数：分类准确率即正确预测数量与总预测数量之比。
定义evaluate_accuracy(data_iter, net)可以评价模型net在数据集data_iter上的准确率。

（五）训练模型：
梳理一下使用小批量随机梯度下降来优化模型的损失函数

def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None)

在一个周期之内，
①首先初始化参数train_l_sum, train_acc_sum, n
②利用softmax回归模型net()预测输出y_hat,并且计算损失函数loss()，然后将元素求和sum()
③利用backward()对标量l求梯度,然后利用sgd()更新参数
④利用 train_l_sum对损失l，train_acc_sum对正确预测数量，n对总数量来迭代求和，test_acc直接是利用evaluate_accuracy(data_iter, net)求评价模型net在数据集data_iter上的准确率。
⑤周期完成，求均值。

最后学习第三章第七节–softmax回归的简洁实现
按照线性回归的简洁实现中的介绍：
①先定义一个模型变量net，它是一个Sequential实例。在Gluon中，Sequential实例可以看作是一个串联各个层的容器。在构造模型时，我们在该容器中依次添加层。当给定输入数据时，容器中的每一层将依次计算并将输出作为下一层的输入。
②在Gluon中，全连接层是一个Dense实例。我们定义该层输出个数为10。
③在使用net前，我们需要初始化模型参数，如线性回归模型中的权重和偏差。我们从MXNet导入init模块。该模块提供了模型参数初始化的各种方法。这里的init是initializer的缩写形式。我们通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为0.01的正态分布。偏差参数默认会初始化为零。
④利用SoftmaxCrossEntropyLoss()计算包括softmax运算和交叉熵损失。由于默认 sparse_label is True，所以计算
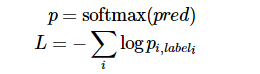⑤同样，我们也无须实现小批量随机梯度下降。在导入Gluon后，我们创建一个Trainer实例，并指定学习率为0.1的小批量随机梯度下降（sgd）为优化算法。该优化算法将用来迭代net实例所有通过add函数嵌套的层所包含的全部参数。这些参数可以通过collect_params函数获取。
最后训练模型。