Python 各种回归（含sklearn）

机器学习
https://www.jb51.net/article/164603.htm
多元回归
https://zhuanlan.zhihu.com/p/61084966?utm_source=wechat_session
正态性检验
https://blog.csdn.net/QimaoRyan/article/details/72861387

# 定义模型预测准确率得分
n_folds = 5
def score(model):
    kf = KFold(n_folds, shuffle=True, random_state=20)
    score=cross_val_score(model,x, y, scoring="accuracy", cv = kf)
    return(score.mean())

一、多元线性回归

调用statsmodels模块中的子模块ols函数。有关该函数的语法及参
数含义可见下方：
ols(formula, data, subset=None, drop_cols=None)
formula：以字符串的形式指定线性回归模型的公式，如’y～x1+x2+x3’（对于非数值的离散变量，建模时必须将其设置为哑变量的效果，实现方式很简单，将该变量套在C()中，表示将其当作分（Category）变量处理即可。即含定性自变量的回归模型）
C()无法选择对照变量（包含在常数中的变量） ，随机选
data：指定建模的数据集。
subset：通过bool类型的数组对象，获取data的子集用于建模。
drop_cols：指定需要从data中删除的变量。

实训任务1：产品利润预测

数据集包含5个变量，分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润，请完成以下任务：
（1）将数据集划分为训练集和测试集，其中测试集占比20%，完成多元线性回归建模；
（2）完成F检验和t检验；
（3）完正态性检验、多重共线性检验、线性相关性检验、异常值检验、独立性检验、方差齐性检验；
（4）使用最终确定的模型进行预测，并画出图形，比较预测值和实际值。

###方法罗列，不是完整顺序
# 工作年限与收入之间的散点图
# 导入第三方模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 导入数据集
income = pd.read_csv(r'C:\Users\Administrator\Desktop\Salary_Data.csv')
# 绘制散点图
sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income, ci = None)
# 显示图形
plt.show()

# 简单线性回归模型的参数求解
# 样本量
n = income.shape[0]
# 计算自变量、因变量、自变量平方、自变量与因变量乘积的和
sum_x = income.YearsExperience.sum()
sum_y = income.Salary.sum()
sum_x2 = income.YearsExperience.pow(2).sum()
xy = income.YearsExperience * income.Salary
sum_xy = xy.sum()
# 根据公式计算回归模型的参数
b = (sum_xy-sum_x*sum_y/n)/(sum_x2-sum_x**2/n)
a = income.Salary.mean()-b*income.YearsExperience.mean()
# 打印出计算结果
print('回归参数a的值：',a)
print('回归参数b的值：',b)

# 导入第三方模块
import statsmodels.api as sm
# 利用收入数据集，构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
# 返回模型的参数值
fit.params



####====== 多元线性回归模型的构建和预测==========
# 导入模块
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'C:\Users\Administrator\Desktop\Predict to Profit.xlsx')
# 将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size = 0.2, random_state=1234)
# 根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + C(State)', data = train).fit()
print('模型的偏回归系数分别为：\n', model.params)
# 删除test数据集中的Profit变量，用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异：\n',pd.DataFrame({
     'Prediction':pred,'Real':test.Profit}))

# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(Profit.State)
# 将哑变量与原始数据集水平合并
Profit_New = pd.concat([Profit,dummies], axis = 1)
# 删除State变量和California变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）
Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)

# 拆分数据集Profit_New
train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)

# 导入第三方模块
import numpy as np
## 计算法：
# 计算建模数据中，因变量的均值
ybar = train.Profit.mean()
# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
# 计算回归离差平方和
RSS = np.sum((model2.fittedvalues-ybar) ** 2)
# 计算误差平方和
ESS = np.sum(model2.resid ** 2)
# 计算F统计量的值
F = (RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)
## 直接得
# 返回模型中的F值
model2.fvalue

### 正态性检验
## 直方图法
# 导入第三方模块
import scipy.stats as stats
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制直方图
sns.distplot(a = Profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {
     'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {
     'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {
     'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

## 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(Profit_New.Profit)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')
# 显示图形
plt.show()

## shapiro检验（数据<5000）
# 导入模块
import scipy.stats as stats
stats.shapiro(Profit_New.Profit)

## K-S检验
# 生成正态分布和均匀分布随机数（随机数据）
rnorm = np.random.normal(loc = 5, scale=2, size = 10000)  #正态分布
runif = np.random.uniform(low = 1, high = 100, size = 10000)  #均匀分布
# 正态性检验
KS_Test1 = stats.kstest(rvs = rnorm, args = (rnorm.mean(), rnorm.std()), cdf = 'norm')
KS_Test2 = stats.kstest(rvs = runif, args = (runif.mean(), runif.std()), cdf = 'norm')
  #rvs：待检验的数据 cdf：检验方法，norm即正态性检验
print(KS_Test1)
print(KS_Test2)

### 多重共线性检验
# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量X(包含RD_Spend、Marketing_Spend和常数列1)
X = sm.add_constant(Profit_New.ix[:,['RD_Spend','Marketing_Spend']])

# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 返回VIF值
vif

### 线性相关性检验
# 计算数据集Profit_New中每个自变量与因变量利润之间的相关系数
Profit_New.drop('Profit', axis = 1).corrwith(Profit_New.Profit)

# 散点图矩阵
# 导入模块
import matplotlib.pyplot as plt
import seaborn
# 绘制散点图矩阵
seaborn.pairplot(Profit_New.ix[:,['RD_Spend','Administration','Marketing_Spend','Profit']])
# 显示图形
plt.show()

### 模型修正（去掉不显著的）
model3 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = train).fit()
# 模型回归系数的估计值
model3.params

### 异常值检验
outliers = model3.get_influence()
# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值（不常用）
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]

# 合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
                     pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
# 重设train数据的行索引
train.index = range(train.shape[0])
# 将上面的统计量与train数据集合并
profit_outliers = pd.concat([train,contat1], axis = 1)
profit_outliers.head()

# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu)>2),1,0))/profit_outliers.shape[0]
outliers_ratio
# 挑选出非异常的观测点
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu)<=2,]

# 应用无异常值的数据集重新建模
model4 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = none_outliers).fit()
model4.params

### 独立性检验
# Durbin-Watson统计量
# 模型概览
model4.summary()

### 方差齐性检验
## 图形法
# 设置第一张子图的位置
ax1 = plt.subplot2grid(shape = (2,1), loc = (0,0))
# 绘制散点图
ax1.scatter(none_outliers.RD_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax1.hlines(y = 0 ,xmin = none_outliers.RD_Spend.min(),xmax = none_outliers.RD_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')

# 设置第二张子图的位置
ax2 = plt.subplot2grid(shape = (2,1), loc = (1,0))
# 绘制散点图
ax2.scatter(none_outliers.Marketing_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax2.hlines(y = 0 ,xmin = none_outliers.Marketing_Spend.min(),xmax = none_outliers.Marketing_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')

# 调整子图之间的水平间距和高度间距
plt.subplots_adjust(hspace=0.6, wspace=0.3)
# 显示图形
plt.show()

## BP检验法（方差齐性）
sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)

### 模型预测
# model4对测试集的预测
pred4 = model4.predict(exog = test.ix[:,['RD_Spend','Marketing_Spend']])
# 绘制预测值与实际值的散点图
plt.scatter(x = test.Profit, y = pred4)
# 添加斜率为1，截距项为0的参考线
plt.plot([test.Profit.min(),test.Profit.max()],[test.Profit.min(),test.Profit.max()],
        color = 'red', linestyle = '--')
# 添加轴标签
plt.xlabel('实际值')
plt.ylabel('预测值')
# 显示图形
plt.show()

实训任务2：上市公司来年盈利状况的预测

本案例随机抽取深市和沪市2002年和2003年各500个样本，对上市公司的净资产收益率（return on equity, ROE）进行预测。
我们要求使用2002年的样本来建立模型，2003年的数据用来检验模型的预测精度。

目标：盈利预测
因变量：下一年的净资产收益率（ROE）
自变量：当年的财务信息
样本容量：2002年500；2003年500

ROEt: 当年净资产收益率
ATO: 资产周转率（asset turnover ratio）
LEV: 债务资本比率（debt to asset ratio）反映公司基本债务状况
PB: 市倍率（price to book ratio）反映公司预期未来成长率
ARR: 应收账款/主营业务收入（account receivable over total income）反映公司的收入质量
PM: 主营业务利润/主营业务收入（profit margin）反映公司利润状况
GROWTH: 主营业务增长率（sales growth rate）反映公司已实现的当年增长率
INV: 存货/资产总计（inventory to asset ratio）反映公司的存货状况
ASSET: （对数）资产总计（log-transformed asset）反映公司的规模

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# 导入数据集
data = pd.read_csv(r'C:\Users\hp\Desktop\roe.csv')

# 将数据集拆分为训练集和测试集
train=data.iloc[0:500]
test=data.iloc[500:]

# 根据train数据集建模
model = sm.formula.ols('ROE~ROEt+ATO+PM+LEV+GROWTH+PB+ARR+INV+ASSET', data = train).fit()
print('模型的偏回归系数分别为：\n', model.params)
model.summary()
'''
ROEt、LEV、GROWTH系数显著
'''

### 线性相关性检验
## 计算每个自变量与因变量利润之间的Marketin相关系数
data.drop('ROE', axis = 1).corrwith(data.ROE)
'''
自变量中ROEt、LEV与ROE相关系数较高，分别为0.572和0.297
'''

## 散点图矩阵
sns.pairplot(data.ix[:,['ROEt','ATO','PM','LEV','GROWTH','PB','ARR','INV','ASSET','ROE']])
# 显示图形
plt.show()
'''
ROEt和ROE之间的散点图几乎为一条向上倾斜的直线，说明这两种变量之间确实存在很强的线性相关,其余关系不明显
'''

### 模型修正
model2 = sm.formula.ols('ROE ~ ROEt + LEV', data = train).fit()
model2.params

### 异常值检验
outliers = model2.get_influence()
# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]
# 合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
                     pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
# 重设train数据的行索引
train.index = range(train.shape[0])
# 将上面的统计量与train数据集合并
data_outliers = pd.concat([train,contat1], axis = 1)
data_outliers.head()
# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(data_outliers.resid_stu)>2),1,0))/data_outliers.shape[0]
outliers_ratio
'''
异常比例为1.4%，比较小，故考虑将其删除。
'''

# 挑选出非异常的观测点
none_outliers = data_outliers.ix[np.abs(data_outliers.resid_stu)<=2,]

### 应用无异常值的数据集重新建模
model3 = sm.formula.ols('ROE ~ ROEt + LEV', data = none_outliers).fit()
model3.params
'''
新的模型公式为：ROE = 0.3838 + 0.5445 ROEt - 0.0305 LEV
当年净资产收益率和债务资本比率对下一年的净资产收益率有影响，其中当年净资产收益率影响较大。
'''

### 显著性检验
# 返回模型中的F值
model3.fvalue
'''
184.38006651692137
'''
# 导入模块
from scipy.stats import f
# 统计变量个数和观测个数
p = model3.df_model
n = none_outliers.shape[0]
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)
'''
3.0141222778120325
计算出的F统计值大于理论F值，拒绝原假设，即认为多元线性回归是显著的，也就是回归模型的偏回归系数不全为0。
'''
# 模型的概览信息
model3.summary()
'''
t检验中P值都小于0.05，说明变量都通过系数的显著性检验。
'''

### 正态性检验
## 直方图法
import scipy.stats as stats
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制直方图
sns.distplot(a = none_outliers.ROE, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {
     'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {
     'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {
     'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()
'''
核密度曲线和正态分布密度曲线的趋势比较吻合，直观上可以认为变量服从正态分布
'''

## 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(none_outliers.ROE)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')
# 显示图形
plt.show()
'''
不管是PP图还是QQ图，绘制的散点均落在直线的附近，没有较大的偏离，变量近似服从正态分布
'''

# shapiro检验
import scipy.stats as stats
stats.shapiro(none_outliers.ROE)
'''
shapiro检验的p值为0.629，不拒绝原假设，服从正态分布
'''

### 多重共线性检验
# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量X(包含ROEt、LEV和常数)
X = sm.add_constant(none_outliers.ix[:,['ROEt','LEV']])
# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 返回VIF值
vif
'''
两个自变量对应的方差膨胀因子均小于10，说明构建模型的数据并不存在多重共线性。
'''

### 残差的独立性检验
# Durbin-Watson统计量
# 模型概览
model3.summary()
'''
DW统计量的值为1.959，比较接近于2，故可以认为模型的残差项之间是满足独立性这个假设前提的。
'''

### 方差齐性检验
# BP检验
sm.stats.diagnostic.het_breushpagan(model3.resid, exog_het = model3.model.exog)
'''
LM统计量和F统计量的p值均为0.98，不拒绝原假设，说明残差方差为常数，残差项满足方差齐性的假设
'''

### 模型预测
# model3对测试集的预测
pred2 = model3.predict(exog = test.ix[:,['ROEt','LEV']])
# 绘制预测值与实际值的散点图
plt.scatter(x = test.ROE, y = pred2)
# 添加斜率为1，截距项为0的参考线
plt.plot([test.ROE.min(),test.ROE.max()],[test.ROE.min(),test.ROE.max()],
        color = 'red', linestyle = '--')
# 添加轴标签
plt.xlabel('real')
plt.ylabel('pred')
# 显示图形
plt.show()

实训任务3：北京房价影响因素探究及预测

注：案例残差不符合正态性分布，只看过程
问题：1.先将分类变量做方差分析，把显著变量加入模型用机器学习更好
2.分类变量不用做多重共线性
3.不能删分类变量里单个类别

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm

# 导入数据集
train = pd.read_csv(r'C:\Users\hp\Desktop\real.csv',encoding='gbk')
test = pd.read_csv(r'C:\Users\hp\Desktop\new.csv',encoding='gbk')

# 根据train数据集建模
model = sm.formula.ols('price~rong+lv+area+ratio+C(dis)+C(ring)+C(wuye)+C(fitment)+C(contype)', data = train).fit()
print('模型的偏回归系数分别为：\n', model.params)
# 预测
pred = model.predict(exog = test)

### 生成哑变量
dummies1 = pd.get_dummies(train.dis)
dummies2 = pd.get_dummies(train.ring)
dummies3 = pd.get_dummies(train.wuye)
dummies4 = pd.get_dummies(train.fitment)
dummies5 = pd.get_dummies(train.contype)
# 将哑变量与原始数据集水平合并
train2 = pd.concat([train,dummies1,dummies2,dummies3,dummies4,dummies5], axis = 1)
test2 = pd.concat([test,dummies1,dummies2,dummies3,dummies4,dummies5], axis = 1)
# 删除变量
train2.drop(labels = ['dis','ring','wuye','fitment','contype','东城','三至四环','公寓','毛坯','塔楼'], axis = 1, inplace = True)
test2.drop(labels = ['dis','ring','wuye','fitment','contype','东城','三至四环','公寓','毛坯','塔楼'], axis = 1, inplace = True)

### 建模
X=train2.ix[:,1:]
y=train2.price
model2 = sm.OLS(y,X).fit()
print('模型的偏回归系数分别为：\n', model2.params)
model2.summary()
'''
lv、ratio、宣武、崇文、朝阳、海淀、二环以内、二至三环、五环以外、四至五环、精装修的系数显著
'''

### 线性相关性检验
# 计算每个自变量与因变量之间的Marketin相关系数
train2.drop('price', axis = 1).corrwith(train2.price)
'''
自变量中ratio、二至三环、四至五环、五环以外、普通住宅、精装修相关系数较高，分别为0.31、0.29、0.30、0.35、-0.53、0.50
'''

### 模型修正
model3 = sm.formula.ols('price~ratio+二至三环+四至五环+五环以外+精装修', data = train2).fit()
print('模型的偏回归系数分别为：\n', model3.params)

### 异常值检验
outliers = model3.get_influence()
# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]
# 合并各种异常值检验的统计量值
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
                     pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
# 重设train数据的行索引
train2.index = range(train2.shape[0])
# 将上面的统计量与train数据集合并
data_outliers = pd.concat([train2,contat1], axis = 1)
data_outliers.head()
# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(data_outliers.resid_stu)>2),1,0))/data_outliers.shape[0]
outliers_ratio
'''
异常比例为4.5%，比较小，故考虑将其删除。
'''

# 挑选出非异常的观测点
none_outliers = data_outliers.ix[np.abs(data_outliers.resid_stu)<=2,]
train3 = none_outliers.ix[:,0:21]

### 应用无异常值的数据集重新建模
model4 = sm.formula.ols('price~ratio+二至三环+四至五环+五环以外+精装修', data = train3).fit()
print('模型的偏回归系数分别为：\n', model4.params)
'''
影响价格的主要因素有小区停车位住户比例、所在环线、装修状况。和三至四环相比，二至三环的价格821.3，四至五环低1704.3，五环以外低3403.4。和毛坯相比，精装修价格高2597.8.
'''

### 显著性检验
# 返回模型中的F值
model4.fvalue
'''
54.664299539241384
'''
# 导入模块
from scipy.stats import f
# 统计变量个数和观测个数
p = model4.df_model
n = train3.shape[0]
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)
'''
2.262937383111096
计算出的F统计值大于理论F值，拒绝原假设，即认为多元线性回归是显著的，也就是回归模型的偏回归系数不全为0。
'''
# 模型的概览信息
model4.summary()
'''
t检验中ROEt和LEV的P值都小于0.05，说明变量都通过系数的显著性检验。
'''

### 正态性检验
## 直方图法
import scipy.stats as stats
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制直方图
sns.distplot(a = train3.price, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {
     'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {
     'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {
     'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()
'''
核密度曲线和正态分布密度曲线的趋势相差较大，直观上可以认为变量不服从正态分布
'''

## 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(train3.price)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
plt.title('Q-Q图')
# 显示图形
plt.show()
'''
不管是PP图还是QQ图，绘制的散点未落在直线的附近，有较大的偏离，变量不服从正态分布
'''

# shapiro检验
import scipy.stats as stats
stats.shapiro(train3.price)
'''
shapiro检验的p值小于0.05，拒绝原假设，不服从正态分布
'''

### 多重共线性检验
# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量X(包含ROEt、LEV和常数)
X = sm.add_constant(train3.ix[:,['ratio','二至三环','四至五环','五环以外','精装修']])
# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 返回VIF值
vif
'''
自变量对应的方差膨胀因子均小于10，说明构建模型的数据并不存在多重共线性。
'''

### 残差的独立性检验
# Durbin-Watson统计量
# 模型概览
model4.summary()
'''
DW统计量的值为1.697，比较接近2，故可以认为模型的残差项之间是满足独立性这个假设前提的。
'''

### 方差齐性检验
# BP检验
sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)
'''
LM统计量和F统计量的p值均为0.002，拒绝原假设，说明残差方差不是常数，残差项不满足方差齐性的假设
'''

# 模型预测
# model4对测试集的预测
pred2 = model4.predict(exog = test2.ix[:,['ratio','二至三环','四至五环','五环以外','精装修']])
'''
6264.21626752804
5866.47732152316
6131.636618859747
8641.082289281629
'''

二、Logistic回归（0-1）

案例：

手机设备搜集的用户运动数据为例，判断用户所处的运动状态，即步行还是跑步。该数据集一共包含88 588条记录，6个与运动相关的自变量，其中三个与运动的加速度有关，另三个与运动方向有关。接下来将利用该数据集构建Logistic回归模型，并预测新样本所属的运动状态。

###Logistic回归sklearn库
# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import linear_model
from sklearn import model_selection
# 读取数据
sports = pd.read_csv(r'Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.ix[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)
# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数
print(sklearn_logistic.intercept_, sklearn_logistic.coef_)
sklearn_logistic.score(X_train, y_train)
# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)
# 预测结果统计
pd.Series(sklearn_predict).value_counts()
# 导入第三方模块
from sklearn import metrics

# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
cm
Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict)
Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict)
Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print('模型准确率为%.2f%%:' %(Accuracy*100))
print('正例覆盖率为%.2f%%' %(Sensitivity*100))
print('负例覆盖率为%.2f%%' %(Specificity*100))

# 混淆矩阵的可视化
# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
# 绘制热力图
sns.heatmap(cm, annot = True, fmt = '.2e',cmap = 'GnBu')
# 图形显示
plt.show()

### ROC曲线
# y得分为模型预测正例的概率
y_score = sklearn_logistic.predict_proba(X_test)[:,1]
# 计算不同阈值下，fpr和tpr的组合值，其中fpr表示1-Specificity，tpr表示Sensitivity
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

###--------------------- logistic回归stastmodels库 ---------------------- #
# 导入第三方模块
import statsmodels.api as sm
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)
# 为训练集和测试集的X矩阵添加常数列1
X_train2 = sm.add_constant(X_train)
X_test2 = sm.add_constant(X_test)
# 拟合Logistic模型
sm_logistic = sm.formula.Logit(y_train, X_train2).fit()
# 返回模型的参数
sm_logistic.params
# -----------------------第二步 预测构建混淆矩阵 ----------------------- #
# 模型在测试集上的预测
sm_y_probability = sm_logistic.predict(X_test2)###注意这个预测值和上一种方法的不同
# 根据概率值，将观测进行分类，以0.5作为阈值
sm_pred_y = np.where(sm_y_probability >= 0.5, 1, 0)
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sm_pred_y, labels = [0,1])
cm
# -----------------------第三步 绘制ROC曲线 --------------------- #
# 计算真正率和假正率 
fpr,tpr,threshold = metrics.roc_curve(y_test, sm_y_probability)
# 计算auc的值  
roc_auc = metrics.auc(fpr,tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

0-1因变量回归的练习：上市公司是否被ST

数据共包含1430个完整的观测。其中，684个观测来自1999年，即解释性变量来自1999年，我们用这部分数据建立模型。剩下的746个观测来自2000年，我们用这部分数据检验模型的预测效果。
因变量是什么？
若解释变量来自1999年，那么因变量ST就是2002是否被宣布ST；
若解释变量来自2000，那么因变量ST就是2003年是否被宣布ST。

ARA:应收账款与总资产的比例，衡量盈利质量
ASSET：对数变换后的资产规模，用于反映公司规模
ATO:资产周转率，用于度量资产利用效率
GROWTH:销售收入增长率，用于反映公司的成长潜力
LEV:负债资产比率，用于反映债务状况
ROA：资产收益率，用于度量盈利能力
SHARE:最大股东的持股比例，用于反映股权结构

###Logistic回归sklearn库
# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import linear_model
from sklearn import model_selection

# 读取数据
data = pd.read_csv(r'C:\Users\hp\Desktop\ST.csv')

# 选取训练集测试集
train = data.loc[data['year'] == 1999] 
test = data.loc[data['year'] == 2000] 

X_train=train.drop(labels =['year','ST'], axis = 1, inplace = False)
y_train=train.ST
X_test=test.drop(labels =['year','ST'], axis = 1, inplace = False)
y_test=test.ST

# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数
print(sklearn_logistic.intercept_, sklearn_logistic.coef_)
'''
[-0.37145315] [[ 1.53047657 -0.11348713 -0.50267722 -0.89698116  1.30174923 -0.24722824
  -0.0129398 ]]
ARA和LEV的系数较大
'''
sklearn_logistic.score(X_train, y_train)
'''
 0.9473684210526315
 '''
 
# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)
# 预测结果统计
pd.Series(sklearn_predict).value_counts()
'''
746个0
'''

# 导入第三方模块
from sklearn import metrics
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
cm
'''
[699,   0]
[ 47,   0]
'''
Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict)
Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict)
Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print('模型准确率为%.2f%%:' %(Accuracy*100))
print('正例覆盖率为%.2f%%' %(Sensitivity*100))
print('负例覆盖率为%.2f%%' %(Specificity*100))
'''
模型准确率为93.70%:
正例覆盖率为0.00%
负例覆盖率为100.00%
'''

# 混淆矩阵的可视化
# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
# 绘制热力图
sns.heatmap(cm, annot = True, fmt = '.2e',cmap = 'GnBu')
# 图形显示
plt.show()

### ROC曲线
# y得分为模型预测正例的概率
y_score = sklearn_logistic.predict_proba(X_test)[:,1]
# 计算不同阈值下，fpr和tpr的组合值，其中fpr表示1-Specificity，tpr表示Sensitivity
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)
'''
0.7462636593309592
'''

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

三、泊松回归

案例：

该案例来源于我国北方某城市处于垄断地位的一家超市，数据包含了该超市一部分会员的详细消费记录。我们以某年某月为基准月份（第0月），因此，可以将前一个月记为第-1月，以此类推。我们的因变量是一个会员在基准月份光顾该超市的次数，因此是一个典型的技术计数数据。超市经理所感兴趣的问题是能否从这些会员前三个月的消费记录中找出什么规律，以便判断超市的众多会员中哪些人在这个月还会光顾超市以及大约会光顾多少次。为此，我们整理了每一个会员前三个月的每月光顾次数以及每月的消费金额。数据包含3995个有效样本。

# possion回归（结果是转化好的纳么哒（均值）的值）
import pandas as pd
from statsmodels.formula.api import poisson
crm = pd.read_csv(r'crm.csv')
model=poisson(formula="freq0~freq1+freq2+freq3+exp1+exp2+exp3",data=crm)
results = model.fit()
print(results.summary())
crm1 = pd.read_csv(r'crm1.csv')
print(results.predict(crm1))

注意：零膨胀和过散布问题

四、岭回归+lasso回归

https://blog.csdn.net/weixin_42521211/article/details/105806200

实训：中国民航客运量的回归

为了研究我国民航客运量的变化趋势及其成因，我们以民航客运量为因变量，所有变量如下：
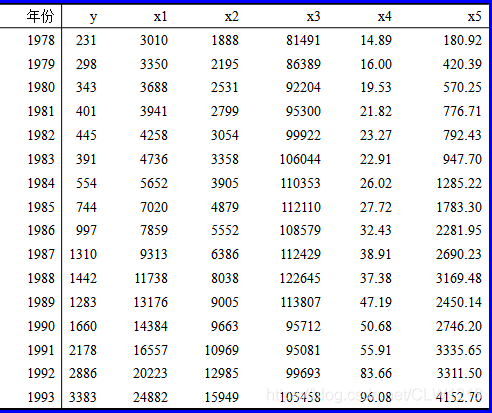
y—民航客运量(万人)；x1—国民收入(亿元)；x2—消费额(亿元)；x3—铁路客运量(万人)；x4—民航航线里程(万公里)；x5—来华旅游入境人数(万人)。
根据《1994年统计摘要》获得1978-1993年统计数据
要求：
1、使用岭回归和LASSO回归寻找最优的λ值；
2、根据系数随λ值变化的可视化曲线，提出存在多重共线性的变量，再次建模，写出最终模型。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import Ridge
import warnings
warnings.filterwarnings("ignore")   # 忽略警告信息输出

# 读取数据
data = pd.read_csv(r'C:\Users\hp\Desktop\data.csv',encoding='gbk')

# 选择自变量、因变量
X,y = data.ix[:,2:],data.ix[:,1]

# 将数据集拆分为训练集、测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size=0.2,random_state=123)

#======================岭回归==========================
##====== 可视化方法=======
# 构造不同的 lambda值
lambds = np.logspace(-5,2,200)
# 构造空列表，用于存储模型的偏回归系数
ridge_coffs = []
# 求解不同lambda对应的系数值
for lambd in lambds:
    ridge = Ridge(alpha=lambd,normalize=True)
    ridge.fit(X_train,y_train)
    ridge_coffs.append(ridge.coef_)

# 绘制lambda的对数与回归系数的关系
# 设置绘图风格
plt.style.use('seaborn')
# 为了画图中文可以正常显示
plt.rcParams['font.sans-serif'] = ['SimHei'] #指定默认字体
plt.rcParams['axes.unicode_minus'] = False  #解决保存图像时负号'-'显示为方块的问题

plt.plot(lambds,ridge_coffs)
# 对x轴做对数处理
plt.xscale('log')
# 设置x轴和y轴标签
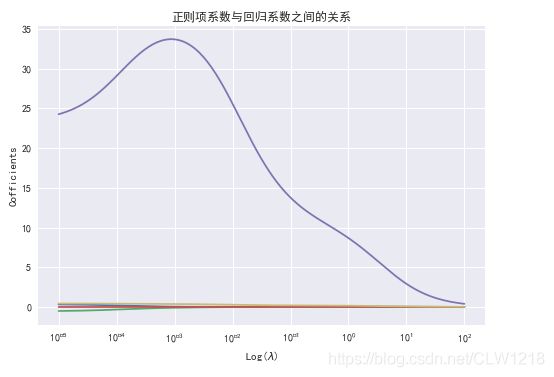
plt.xlabel('Log($\lambda$)')
plt.ylabel('Cofficients')
plt.title('正则项系数与回归系数之间的关系')
# 显示图形
plt.show()
'''
由图，x1存在多重共线性，删除变量
'''

# 删除多重共线性变量
X_train.drop('x1',axis=1,inplace=True)
X_test.drop('x1',axis=1,inplace=True)

# 再进行一次可视化
lambds = np.logspace(-2,2,200)
ridge_coffs = []
for lambd in lambds:
    ridge = Ridge(alpha=lambd,normalize=True)
    ridge.fit(X_train,y_train)
    ridge_coffs.append(ridge.coef_)
plt.style.use('seaborn')
plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.rcParams['axes.unicode_minus'] = False  
plt.plot(lambds,ridge_coffs)
plt.xscale('log')
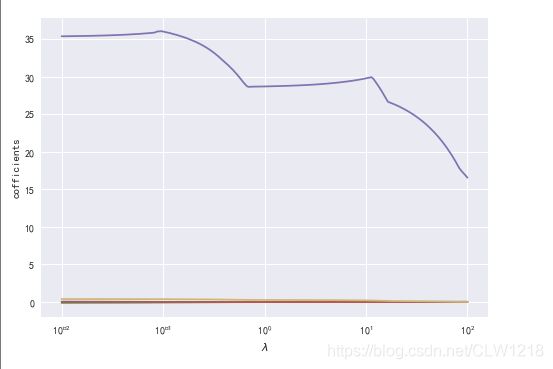
plt.xlabel('Log($\lambda$)')
plt.ylabel('Cofficients')
plt.title('正则项系数与回归系数之间的关系')
plt.show()
'''
消除了多重共线性，lambd在***时系数趋于平缓
'''

# 交叉验证法确定λ值
from sklearn.linear_model import RidgeCV
ridge_cv = RidgeCV(alphas=lambds,normalize=True,scoring='neg_mean_squared_error',cv=10)
# 模型拟合
ridge_cv.fit(X_train,y_train)
# 返回最佳的lambda值
ridge_best_lambda = ridge_cv.alpha_
print('最佳的lambda值为：',ridge_best_lambda)
'''
最佳的lambda值为：***
'''

# 基于最佳的lambda值建模
ridge = Ridge(alpha=ridge_best_lambda,normalize=True)
ridge.fit(X_train,y_train)
# 返回岭回归模型系数
ridge_coef = pd.Series(data=[ridge.intercept_]+ridge.coef_.tolist(),index =['Intercept']+list(X_train.columns))
print('岭回归模型系数:\n',ridge_coef)
'''
岭回归模型系数:
 Intercept    630.867929
x1             0.057979
x2             0.075966
x3            -0.009156
x5             0.216515
'''

# 模型预测
from sklearn.metrics import mean_squared_error # 均方误差MSE，评估模型效果
y_pred = ridge.predict(X_test)
# 预测效果验证  :均方根误差RMSE
rmse = np.sqrt(mean_squared_error(y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)
'''
测试集均方根误差RMSE： 46.77979596227859
'''

#======================lasso回归==========================
data = pd.read_csv(r'C:\Users\hp\Desktop\data.csv',encoding='gbk')
# 选择自变量、因变量
X,y = data.ix[:,2:],data.ix[:,1]
# 将数据集拆分为训练集、测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size=0.2,random_state=123)

# 导入模块中的函数
from sklearn.linear_model import Lasso

lambds = np.logspace(-2,2,200)
# 空列表，用于存储模型的偏回归系数
lasso_coffs = []
for lambd in lambds:
    lasso = Lasso(alpha=lambd,normalize=True)
    lasso.fit(X_train,y_train)
    lasso_coffs.append(lasso.coef_)
# 绘制lambda与回归系数的折线图
plt.plot(lambds,lasso_coffs)
# 对x轴取对数
plt.xscale('log')
plt.xlabel('$\lambda$')
plt.ylabel('cofficients')
plt.show()

# 交叉验证
from sklearn.linear_model import LassoCV
lasso_cv = LassoCV(alphas=lambds,normalize=True,cv=10)
lasso_cv.fit(X_train,y_train)
# 输出最佳的lambda值
lasso_best_alpha = lasso_cv.alpha_
print("最佳lambda值：",lasso_best_alpha)
'''
最佳lambda值： 0.0174263338600965
'''

# 基于最佳的lambda值建模
lasso = Lasso(alpha=lasso_best_alpha,normalize=True)
lasso.fit(X_train,y_train)
# 返回LASSO回归模型系数
lasso_coef = pd.Series(data=[lasso.intercept_]+lasso.coef_.tolist(),index =['Intercept']+list(X_train.columns))
print('lasso回归模型系数:\n',lasso_coef)
'''
lasso回归模型系数:
 Intercept    869.509333
x1             0.039523
x2            -0.130325
x3            -0.013593
x4            35.452554
x5             0.392240
'''

# 模型预测
from sklearn.metrics import mean_squared_error 
y_pred = lasso.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)
'''
测试集均方根误差RMSE： 133.57521496736558
'''

岭回归

去重

lasso

五、主成分回归

案例分析：

###===================主成分求解示例=====================
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
newX = pca.fit_transform(X)
print(X)
print(newX)
print(pca.explained_variance_ratio_)
pca = PCA(n_components=1)
newX = pca.fit_transform(X)
print(pca.explained_variance_ratio_)

##主成分回归示例
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
#  读取数据
data = pd.read_csv('data.csv' , encoding =  'UTF-8') 
data
X = data.iloc[:, 0:4]
Y = data.iloc[:, 5]
# 对数据进行标准化
X = (X - X.mean())/np.std(X)
Y = (Y - Y.mean())/np.std(Y)
# 对数据进行分割
X_train, X_test, Y_train, Y_test = train_test_split(X,Y,train_size=0.7, random_state=1)
# 创建pca模型
pca = PCA(n_components='mle')
# 对模型进行训练
pca.fit(X_train)
# 返回降维后据
X_train = pca.transform(X_train)
X_train # 经过降维之后的主成分矩阵----> 用来进行主成分回归的数
Y_train= (Y_train - Y_train.mean())/np.std(Y)
Y_train
# 使用返回后的数据用线性回归模型进行建模
import statsmodels.api as sm
ols = sm.OLS(Y_train, X_train).fit()
ols.summary()
pca.explained_variance_ratio_
pca.get_params()
pca.get_precision()  ##不太明白为什么是四行四列。代表什么
# 使用LinearRegression进行拟合，其实这两种拟合的都差不多
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,Y_train)   # 模型训练
lr.score(X_train, Y_train) # 获取模型的得分
X_test = (X_test - X_test.mean())/np.std(X_test)
X_test = pca.transform(X_test)
X_test
y_pred = lr.predict(X_test)
Y_test
y_pred
plt.scatter(y_pred, Y_test)
plt.xlabel('The predicted Y of LinearRegression')
plt.ylabel('The real Y')
olsr = sm.OLS(y_pred, Y_test).fit()
olsr.summary()

###==================偏最小二乘法===================
from sklearn.cross_decomposition import PLSRegression
X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [2.,5.,4.]]
Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
pls2 = PLSRegression(n_components=2)
pls2.fit(X, Y)
Y_pred = pls2.predict(X)
pls2.fit_transform(X,Y)
pls2.get_params()
pls2.score(X,Y)
pls2.coef_
pls2.x_weights_
from sklearn.cross_decomposition import PLSRegression
import numpy as np
import pandas as pd
from statsmodels import api as sms
data = pd.read_csv('data8.2.csv' , encoding =  'UTF-8') 
data
X = data.iloc[:, 1:14]
Y = data.iloc[:, 0]
pls2 = PLSRegression(n_components=3)
pls2.fit(X, Y)
pls2.fit_transform(X,Y)
pls2.get_params()
pls2.score(X,Y)
pls2.coef_
pls2.x_weights_
pls2.y_weights_
pls2.x_loadings_
pls2.x_scores_
pls2.n_iter_

实训

糖尿病数据集。该数据集包含442条观测、10个自变量和1个因变量。这些自变量分别为患者的年龄、性别、体质指数、平均血压及六个血清测量值；因变量为糖尿病指数，其值越小，说明糖尿病的治疗效果越好。根据文献可知，对于胰岛素治疗糖尿病的效果表明，性别和年龄对治疗效果无显著影响。
请以4：1的比例划分训练集和测试集，然后分别使用主成分回归和偏最小二乘回归对本题进行做出分析，找出模型得分最高的主成分个数及系数，再使用测试集计算此时的RMSE，对比两种算法。

import pandas as pd
import numpy as np

data = pd.read_excel(r'C:\Users\hp\Desktop\diabetes.xlsx')

data.drop(['AGE','SEX'],axis=1,inplace=True)
X,Y = data.ix[:,:-1],data.ix[:,-1]

# 对数据进行标准化
X = (X - X.mean())/np.std(X)
Y = (Y - Y.mean())/np.std(Y)

# 将数据集拆分为训练集、测试集
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.2,random_state=123)
               
###==================主成分回归====================
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
# 创建pca模型
pca = PCA(n_components=8)  # 8时模型得分最高
# 对模型进行训练
pca.fit(X_train)
# 返回降维后数据
X_train = pca.transform(X_train)
X_train 
Y_train= (Y_train - Y_train.mean())/np.std(Y)
Y_train

# 线性回归模型
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,Y_train)   
lr.score(X_train, Y_train) # 获取模型的得分
'''
0.48598326062077973
'''
lr.coef_
X_test = (X_test - X_test.mean())/np.std(X_test)
X_test = pca.transform(X_test)

# 模型预测
from sklearn.metrics import mean_squared_error # 均方误差MSE，评估模型效果
y_pred = lr.predict(X_test)
rmse = np.sqrt(mean_squared_error(Y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)
'''
测试集均方根误差RMSE： 0.6954947256191752
'''

###====================偏最小二乘法======================
from sklearn.cross_decomposition import PLSRegression
from statsmodels import api as sms

pls2 = PLSRegression(n_components=8)
pls2.fit(X_train,Y_train)
pls2.fit_transform(X_train,Y_train)
pls2.get_params()
pls2.score(X_train,Y_train)  
'''
 0.4859832606207598
 '''
pls2.coef_

# 模型预测
from sklearn.metrics import mean_squared_error # 均方误差MSE，评估模型效果
y_pred = pls2.predict(X_test)
rmse = np.sqrt(mean_squared_error(Y_test,y_pred))
print("测试集均方根误差RMSE：",rmse)
'''
测试集均方根误差RMSE：0.6954947287521299
'''
'''
主成分回归模型更好
'''

六、多项式回归

# 二次多项式回归
# 实例化一个二次多项式特征实例
quadratic_featurizer=PolynomialFeatures(degree=2)
# 用二次多项式对样本X值做变换
X_train_quadratic = quadratic_featurizer.fit_transform(X)
# 创建一个线性回归实例
regressor_model=linear_model.LinearRegression()
# 以多项式变换后的x值为输入，带入线性回归模型做训练
regressor_model.fit(X_train_quadratic,y)
regressor_model.coef_  ##显示系数
# 设计x轴一系列点作为画图的x点集
xx=np.linspace(30,400,100)
# 把训练好X值的多项式特征实例应用到一系列点上,形成矩阵
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
yy_predict = regressor_model.predict(xx_quadratic)
# 用训练好的模型作图
plt.plot(xx, yy_predict, 'r-')
X_test_quadratic = quadratic_featurizer.transform(X_test)
print('二次回归     r-squared', regressor_model.score(X_test_quadratic, y_test))
# plt.show()  # 展示图像

# 三次回归
cubic_featurizer = PolynomialFeatures(degree=3)
X_train_cubic = cubic_featurizer.fit_transform(X)
regressor_cubic = LinearRegression()
regressor_cubic.fit(X_train_cubic, y)
regressor_cubic.coef_   ##显示系数
xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_cubic.predict(xx_cubic))
X_test_cubic = cubic_featurizer.transform(X_test)
print('三次回归     r-squared', regressor_cubic.score(X_test_cubic, y_test))
plt.show()  # 展示图像

七、非线性回归

案例

##非线性最小二乘拟合
from scipy import optimize
import numpy as np
xdata = np.linspace(-10, 10, num=20)
def f2(x, a, b):         # 拟合函数式
    return a*x**2 + b*np.sin(x)
ydata = f2(xdata,2,1) + np.random.randn(xdata.size)    # y
guess = [2, 2]  # 猜测的初始值
params,params_covariance= optimize.curve_fit(f2, xdata, ydata,guess)
print(params)
print(params_covariance) # 协方差矩阵

xdata = np.linspace(0,2*np.pi,1000)
def func(x,A,k,theta):
    return A*np.sin(2*np.pi*k*x+theta)
ydata = func(xdata,10,0.34,np.pi/6) + np.random.randn(xdata.size)
guess=[3,3,3]
params,params_covariance= optimize.curve_fit(func, xdata, ydata,guess)
print(params)
print(params_covariance)

'''
使用最小二乘法拟合正弦函数
'''
import numpy as np
from scipy.optimize import leastsq
import  matplotlib.pyplot as plt 

#定义拟合函数图形
def func(x,p):
    A,k,theta = p
    return A*np.sin(2*np.pi*k*x+theta)
#定义误差函数
def error(p,x,y):
    return y-func(x,p)
#生成训练数据
#随机给出参数的初始值
p0 = [10,0.34,np.pi/6]
A,k,theta = p0
x = np.linspace(0,2*np.pi,1000)
#随机指定参数
y0 = func(x,[A,k,theta])
#randn(m)从标准正态分布中返回m个值，在本例作为噪声
y1 = y0 + 2*np.random.randn(len(x))
#进行参数估计
Para = leastsq(error,p0,args=(x,y1))
A,k,theta = Para[0]
print('A=',A,'k=',k,'theta=',theta)

'''
图形可视化
'''
plt.figure(figsize=(20,8))
ax1 = plt.subplot(2,1,1)
ax2 = plt.subplot(2,1,2)
#在ax1区域绘图
plt.sca(ax1)
#绘制散点图
plt.scatter(x,y1,color='red',label='Sample Point',linewidth = 3)
plt.xlabel('x')
plt.xlabel('y')
y = func(x,p0)
plt.plot(x,y0,color='black',label='sine',linewidth=2)
#在ax2区域绘图
plt.sca(ax2)
e = y-y1
plt.plot(x,e,color='orange',label='error',linewidth=1)
#显示图例和图形
plt.legend()
plt.show()

作业

data = pd.read_csv(r'C:\Users\hp\Desktop\data9.5.csv')
x = data.iloc[:,1]
y = data.iloc[:,2]
plt.scatter(x,y,marker='*',color='blue')

def f2(x, k, a, b, c):    # 函数式刑形式
    return k-a*b**(x**c)
    
guess = [15,1,0.5,1]  # 猜测
params,params_covariance= optimize.curve_fit(f2, x, y,guess, maxfev=500000, bounds=(0, [100., 100., 1,100]))  # maxfev：最大拟合次数  bounds：取值范围，大于0，小于……
print(params)
'''
[14.90578281  9.23677568  0.99778541  1.63687107]
'''
print(params_covariance) 

自变量有多个时的写法

# 乘性
from sklearn.linear_model import LinearRegression
data = pd.read_csv(r'C:\Users\hp\Desktop\data9.6.csv')

lX = data.iloc[:,5:]
ly = data.iloc[:,4]

model = LinearRegression()
model.fit(lX,ly)
model.coef_
'''
[0.90239268, 0.36054285]
'''
model.intercept_
'''
-2.085893188284622
'''
np.exp(0.90239268) #  2.4654952004600927
np.exp(0.36054285) # 1.4341077086623983

# 加性
k = data.iloc[:,2]
l = data.iloc[:,3]
y = data.iloc[:,1]

def f2(x, A, a, b):
    k,l=x   # 自变量有两个
    return A*(k**a)*(l**b)
    
x=[k,l]
guess = [1,0.5,0.5]  
params,params_covariance= optimize.curve_fit(f2, x, y,guess, maxfev=500000, bounds=(0, [100., 1., 1.]))
print(params)
'''
[0.02047588 0.92237277 0.50483645]
'''
print(params_covariance) 

八、随机森林回归

案例：波斯顿房价

from sklearn.datasets import load_boston
from sklearn.cross_validation import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
boston = load_boston()

print(boston.DESCR)
x = boston.data
y = boston.target

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=33)

RF = RandomForestRegressor(n_estimators=100,random_state=0)
RF.fit(x_train, y_train)

RF.feature_importances_
RF.score(x_train, y_train)
RF.score(x_test, y_test)

yhat_RF=RF.predict(x_test)
r2_score(y_test, yhat_RF) 
cross_val_score(RF, boston.data, boston.target, cv=10
   ,scoring = "neg_mean_squared_error")
mean_squared_error(y_test, yhat_RF)

from sklearn.ensemble import AdaBoostRegressor
AB=AdaBoostRegressor()
# 拟合构造 CART 回归树
AB.fit(x_train, y_train)
AB.score(x_train, y_train)
AB.score(x_test, y_test)
# 预测测试集中的房价
yhat_AB=AB.predict(x_test)
r2_score(y_test, yhat_AB) 
mean_squared_error(y_test, yhat_AB)

from sklearn.tree import DecisionTreeRegressor
DT=DecisionTreeRegressor()
# 拟合构造 CART 回归树
DT.fit(x_train, y_train)
DT.score(x_train, y_train)
DT.score(x_test, y_test)
# 预测测试集中的房价
yhat_DT=DT.predict(x_test)
r2_score(y_test, yhat_DT) 
mean_squared_error(y_test, yhat_DT)

from sklearn.ensemble import ExtraTreesRegressor, GradientBoostingRegressor
# 极端随机森林回归
ETR = ExtraTreesRegressor()
ETR.fit(x_train, y_train)
ETR.score(x_train, y_train)
ETR.score(x_test, y_test)
# 预测 保存预测结果
yhat_ETR = ETR.predict(x_test)
r2_score(y_test, yhat_ETR)
mean_squared_error(y_test, yhat_ETR)
# 梯度提升回归
GBR = GradientBoostingRegressor()
# 训练
GBR.fit(x_train, y_train)
GBR.score(x_train, y_train)
GBR.score(x_test, y_test)
# 预测 保存预测结果
yhat_GBR = GBR.predict(x_test)
r2_score(y_test, yhat_GBR)
mean_squared_error(y_test, yhat_GBR)


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

#以波士顿数据集为例，导入完整的数据集并探索
dataset = load_boston()
dataset.data.shape

#总共506*13=6578个数据
X_full, y_full = dataset.data, dataset.target
n_samples = X_full.shape[0]
n_features = X_full.shape[1]

#np.random.RandomState(0)伪随机数生成器,随机种子为0
rng = np.random.RandomState(0)    
missing_rate = 0.5
n_missing_samples = int(np.floor(n_samples * n_features * missing_rate))

#np.floor向下取整，返回.0格式的浮点数
missing_features = rng.randint(0,n_features,n_missing_samples)
missing_samples = rng.randint(0,n_samples,n_missing_samples)    

#创建含缺失值的数据集X_missing和y_missing
X_missing = X_full.copy()
y_missing = y_full.copy()

#创建缺失值-按缺失值位置赋值np.nan
X_missing[missing_samples,missing_features] = np.nan
'''转换成DataFrame是为了后续方便各种操作，
numpy对矩阵的运算速度快到拯救人生，
但是在索引等功能上却不如pandas来得好用'''
X_missing = pd.DataFrame(X_missing) 

#使用均值进行填补
from sklearn.impute import SimpleImputer

#SimpleImputer()缺失值填补函数
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
X_missing_mean = imp_mean.fit_transform(X_missing)

#使用0进行填补
imp_0 = SimpleImputer(missing_values=np.nan, strategy="constant",fill_value=0)
X_missing_0 = imp_0.fit_transform(X_missing)

#用随机森林预测填补缺失值
X_missing_reg = X_missing.copy()

#特征缺失值累计，按索引升序排序
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values

#循环，按缺失值累计升序，依次填补不同特征的缺失值
for i in sortindex:
    #构建我们的新特征矩阵和新标签
    #含缺失值的总数据集
    df = X_missing_reg 
    #要填充特征作为新标签列
    fillc = df.iloc[:,i] 
    #新的特征矩阵=其余特征列+原来的标签列Y
    df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
    #在新特征矩阵中，对含有缺失值的列，进行0的填补
    df_0 =SimpleImputer(missing_values=np.nan,strategy='constant',
         fill_value=0).fit_transform(df)
    #找出我们的训练集和测试集
    Ytrain = fillc[fillc.notnull()]
    Ytest = fillc[fillc.isnull()]
    Xtrain = df_0[Ytrain.index,:]
    Xtest = df_0[Ytest.index,:]
    #用随机森林回归预测缺失值
    rfc = RandomForestRegressor(n_estimators=100)
    rfc = rfc.fit(Xtrain, Ytrain)
    Ypredict = rfc.predict(Xtest)
    #填入预测值
    X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict

#对填补好的数据依次用随机森林回归建模，取得MSE结果
X = [X_full,X_missing_mean,X_missing_0,X_missing_reg]
mse = []
std = []
for x in X:
    estimator = RandomForestRegressor(random_state=0, n_estimators=100)
    scores = cross_val_score(estimator,x,y_full,scoring='neg_mean_squared_error',
                                cv=5).mean()
    mse.append(scores * -1)

#画条形图
x_labels = ['Full data',
            'Mean Imputation',
            'Zero Imputation',
            'Regressor Imputation']
colors = ['r', 'g', 'b', 'orange']
plt.figure(figsize=(12, 6))
ax = plt.subplot(111)
for i in np.arange(len(mse)):
    ax.barh(i, mse[i],color=colors[i], alpha=0.6, align='center')
ax.set_title('Imputation Techniques with Boston Data')
ax.set_xlim(left=np.min(mse) * 0.9,
            right=np.max(mse) * 1.1)
ax.set_yticks(np.arange(len(mse)))
ax.set_xlabel('MSE')
ax.set_yticklabels(x_labels)
plt.show()