蚁群算法python_机器学习(算法篇)蚁群算法
蚂蚁总能找到食物到窝的最优路径 ;
我们模拟一下过程:
(1) 正常情况下,食物到巢穴,小蚂蚁走直线
![]()
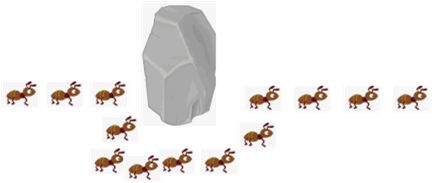
(2) 这时候我们把路打断,放块大石头
(3)路突然中断,小蚂蚁会随机选择一条路行走,向左,向右都会有蚂蚁行走
(4)随着时间的推移, 路程短的线路,行走的蚂蚁越来越多,就会放弃另外一条路
小蚂蚁们是怎么做到的呢 ?
蚁群算法的基本原理:
蚂蚁在路径上释放信息素。
碰到还没走过的路口,就随机挑选一条路走
没找到食物之前,之前自己走过的路,不在走(禁忌路线)
信息素浓度和距离成反比。后来的蚂蚁再次碰到该路口时,就选择信息素浓度较高路径
信息素浓度随着时间因素会散发,
最优路径上的信息素浓度越来越大
最终蚁群找到最优寻食路径
蚁群算法 一些应用场景:
多架无人机战略巡航,路径规划问题
比如出差16个城市,如何规划最优行程,并返回出发点(TSP问题)
上万平米的仓库,如何规划拣货路径,一次行走拣货最多
车辆导航线路规划等等
蚂蚁之间通过信息素 传递信息。
蚂蚁在行走过程中会释放一种称为“信息素”的物质,用来标识自己的行走路径。在寻找食物的过程中,根据信息素的浓度选择行走的方向,并最终到达食物所在的地方。
信息素会随着时间的推移而逐渐挥发。
在一开始的时候,由于地面上没有信息素,因此蚂蚁们的行走路径是随机的。蚂蚁们在行走的过程中会不断释放信息素,标识自己的行走路径。
随着时间的推移,有若干只蚂蚁找到了食物,此时便存在若干条从洞穴到食物的路径。由于蚂蚁的行为轨迹是随机分布的,因此在单位时间内,短路径上的蚂蚁数量比长路径上的蚂蚁数量要多,从而蚂蚁留下的信息素浓度也就越高。
这为后面的蚂蚁们提供了强有力的方向指引,越来越多的蚂蚁聚集到最短的路径上去。
我们在模拟下过程:
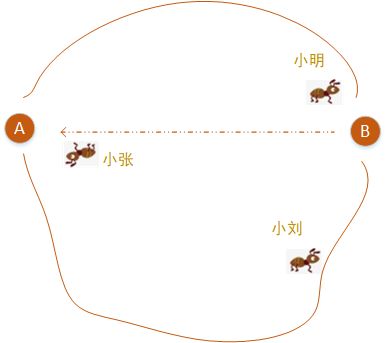
假设到达目的地有三条路,每条路随机选择, 我们假设每条路有一只蚂蚁,假设从A点到B点, 有三条路径可选。(见下图)
假设三条线路关系:
L(小明-线路1) = 2 * L(小张线路2长度)
L(小刘-线路3 ) = 3 * L(小张线路2长度)
2、假设所有蚂蚁的行走速度相同。
假设蚂蚁小张沿着A点到B点, 需要4个单位时间;
3、时间 t =4
小张蚂蚁到达B(终点), 小明蚂蚁2走到一半路程,小刘蚂蚁3走了三分之一的路程
4、时间 t=8
小张蚂蚁又返回A(起点), 小明蚂蚁到达B,小张蚂蚁3走了三分之二的路程
5、 时间t=48:
蚂蚁小张往返于AB之间6次,蚂蚁小明往返于AB间3次,蚂蚁小刘3往返于AB间2次。在不考虑信息素挥发的条件下:三条路径上信息素浓度之比:
D(小张线路2):D(小明线路2):D(小刘线路3)= 6:3:2
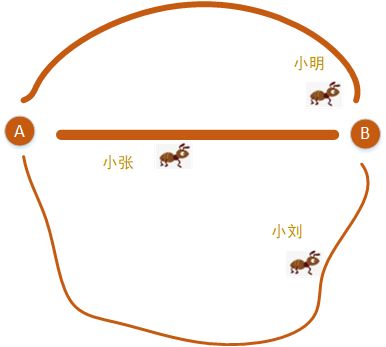
如下图:线越粗,信息素越浓
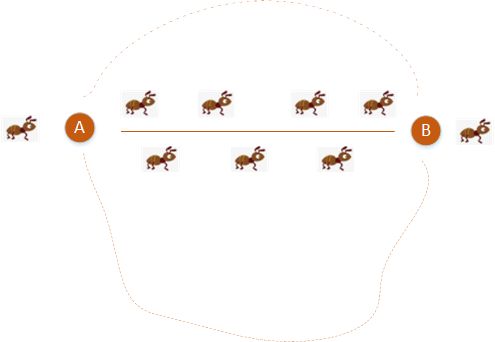
若继续寻找,则按照正反馈机制,最终所有蚂蚁都会选择最短的路径AB,而放弃其他两条路径。
对于单个蚂蚁来说,它并没有要寻找最短路径,只是根据概率选择;对于整个蚁群系统来说,它们却达到了寻找到最优路径的客观上的效果
原理介绍
蚁群算法(Ant Colony Algorithm)最初于1992年由意大利学者M.Dorigo等人提出,它是一种模拟自然界中真实蚁群觅食行为的仿生优化算法。研究发现:每只蚂蚁觅食时在走过的路线上会留下一种称为信息素的物质,蚂蚁之间靠感知这种物质的浓度进行信息传递。蚂蚁在选择路径时总是倾向于朝信息索浓度高的方向移动,而距离短的路径上走过的蚂蚁多,留下的信息素也多,后续蚂蚁选择它的概率也会越大;其他路径上的信息素会随着时间的推移不断挥发,这样就形成了一种正反馈机制,最后整个蚁群聚集到最短路径上。
人工蚁群算法模拟了这一过程。每只蚂蚁在解空间独立地搜索可行解,解越好留下的信息素越多,随着算法推进,较优解路径上的信息素增多,选择它的蚂蚁也随之增多,最终收敛到最优或近似最优的解上。
番外篇1:蚂蚁小知识:
蚂蚁是摔不死的:
体积越小,其表面与重力的比值就越大,这样阻力与重力越趋于平衡。蚂蚁在这种作用力下,就会毫发无伤地降落到地面,不会摔死
番外篇2 :
Dijkstra算法和蚁群算法的区别:
Dijkstra(最短路径)算法和蚁群算法是有着本质不同的,属于两个范畴,前者是确定性算法,输入一个图,必定能产生一个可行结果,得到最短路径。而后者是属于启发式算法,有随机因素。不一定能产生好的结果,但一般情况下由于存在启发式因素和智能因素,能够产生比较好的结果,但不能保证产生全局最优解。
Dijkstra最短路径,所有路径代价都已经提前知道,全局最优解。求出两点之间最优路径。在已知世界找最优解
如下图:图中每个节点的权重(代价)都是已知
蚁群算法 不会穷举,不会遍历所有路径(提前也不知道),探索未知世界,对不确定的未来找最优解。
TSP问题(Travel Salesperson Problem)
TSP问题(旅行商问题)是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次 然后回到出发城市,并要求所走的路程最短。
旅行商问题或者称为中国邮递员问题,是一种NP-hard问题,此类问题用一般的算法是很难得到最优解的,所以一般需要借助一些启发式算法求解,例如遗传算法(GA),蚁群算法(ACO),微粒群算法(PSO)等等。
一个TSP问题可以表达为:求解遍历图G=(V,E,C),所有的节点一次并且回到起始节点,使得连接这些节点的路径成本最低。
线性代数,矩阵没有忘记可以看下,
n个城市,城市到各城市的距离就是n*n的矩阵
式中:V表示蚂蚁K可以选择下一个栅格的集合;
Alpha为信息素浓度启发因子,Alpha越大,表明蚂蚁K越趋向于选择多数蚂蚁走过的路径;
Beta表示期望启发因子,反映了能见度信息对蚂蚁选择下一步位置所起作用的大小,Beta值越大,表明蚂蚁K越趋向于选择距离目标点近的栅格,越倾向于往能见度程。
表示t时刻路径(i,j)上的信息素浓度;
表示t时刻路径(i,j)上的启发信息,其定义为:
蚁群算法的核心部分在于模拟了蚁群的转移概率选择行为,通过使用信息素和启发式函数值进行转移概率计算。
蚁群算法中主要有下面几个参数需要设定
m:整个蚂蚁群体中蚂蚁数量;
n:城市的数量;
dij:城市i与城市j的距离
βij(t):t时刻城市i和城市j连接路径上的信息素;
pkij(t):t时刻蚂蚁k从城市i转移到城市j的概率
蚂蚁数量:
设M表示城市数量,m表示蚂蚁数量。m的数量很重要,因为m过大时,会导致搜索过的路径上信息素变化趋于平均,这样就不好找出好的路径了;m过小时,易使未被搜索到的路径信息素减小到0,这样可能会出现早熟,没找到全局最优解。一般上,在时间等资源条件紧迫的情况下,蚂蚁数设定为城市数的1.5倍较稳妥。
信息素因子:
信息素因子反映了蚂蚁在移动过程中所积累的信息量在指导蚁群搜索中的相对重要程度,其值过大,蚂蚁选择以前走过的路径概率大,搜索随机性减弱;值过小,等同于贪婪算法,使搜索过早陷入局部最优。实验发现,信息素因子选择[1,4]区间,性能较好。
启发函数因子:
启发函数因子反映了启发式信息在指导蚁群搜索过程中的相对重要程度,其大小反映的是蚁群寻优过程中先验性和确定性因素的作用强度。过大时,虽然收敛速度会加快,但容易陷入局部最优;过小时,容易陷入随机搜索,找不到最优解。实验研究发现,当启发函数因子为[3,4.5]时,综合求解性能较好。
信息素挥发因子:
信息素挥发因子表示信息素的消失水平,它的大小直接关系到蚁群算法的全局搜索能力和收敛速度。实验发现,当属于[0.2,0.5]时,综合性能较好。
信息素常数:
这个参数为信息素强度,表示蚂蚁循环一周时释放在路径上的信息素总量,其作用是为了充分利用有向图上的全局信息反馈量,使算法在正反馈机制作用下以合理的演化速度搜索到全局最优解。值越大,蚂蚁在已遍历路径上的信息素积累越快,有助于快速收敛。实验发现,当值属于[10,1000]时,综合性能较好。
最大迭代次数:
最大迭代次数值过小,可能导致算法还没收敛就已结束;过大则会导致资源浪费。一般最大迭代次数可以取100到500次。一般来讲,建议先取200,然后根据执行程序查看算法收敛的轨迹来修改取值。
TSP算法公式备份:
看往期:
机器学习:
机器学习(算法)-随机森林
机器学习(算法篇)-决策树
python篇:
python-基础篇(相忘于江湖)
python-基础篇(子非鱼)
python-基本篇(邯郸学步)
2020-8-5 深圳 暴雨