李宏毅机器学习——课后作业1
李宏毅机器学习视频地址:
【李宏毅 深度学习19(完整版)国语】
第一次作业参考地址:
线性回归预测PM2.5----台大李宏毅机器学习作业1(HW1)
文章目录
-
- 作业要求:
- 作业分析:
- 模型分析:
- 代码分析:
-
- 数据预处理:
- 模型建立:
- 完整代码:
- 运行结果:
作业要求:
给定训练集train.csv,要求根据前9个小时的空气监测情况预测第10个小时的PM2.5含量。
训练集介绍:
- CSV文件,包含台湾丰原地区240天的气象观测资料(取每个月前20天的数据做训练集,12月X20天=240天,每月后10天数据用于测试,对学生不可见);
- 每天的监测时间点为0时,1时…到23时,共24个时间节点;
- 每天的检测指标包括CO、NO、PM2.5、PM10等气体浓度,是否降雨、刮风等气象信息,共计18项;
- 数据集地址:https://pan.baidu.com/s/1o2Yx42dZBJZFZqCa5y3WzQ,提取码:qgtm。
作业分析:
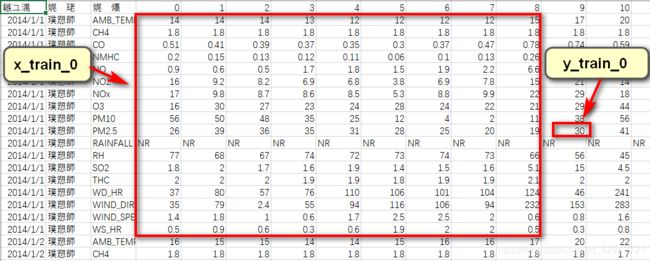
先看tarin.csv,列是监测数据,行是检测项目,共分为18个检测项目,24时的监测数据。
其中比较特殊的数据是RAINFALL,含义是:是否下雨,所以需要将其变成布尔值。
对于该数据,我们需要准备一个二维数组(18,9)来包含每一天的信息。

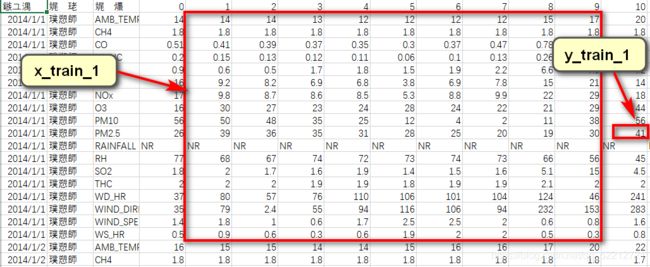
而由于train.csv中给了24时的数据,我们只需要9时数据来预测10时的PM2.5,因此,我们可以用滑动窗口的方法来扩展数据:
这样一来,一天中包含了15个(18,9)的数据帧,共计240天*15=3600个数据帧及其label。
模型分析:
请见:
线性回归预测PM2.5----台大李宏毅机器学习作业1(HW1)
代码分析:
数据预处理:
# 数据预处理
def dataProcess(df):
#建立两个列表,跟数组类似,但当中存放的是索引
x_list, y_list = [], []
# df替换指定元素,将空数据填充为0
df = df.replace(['NR'], [0.0])
# astype() 转换array中元素数据类型
array = np.array(df).astype(float)
# 将数据集拆分为多个数据帧
#从0开始,到4320行,步长为18
for i in range(0, 4320, 18):
#从0列开始,到第15列结束
for j in range(15):
#获取一个二维列表,18行9列
mat = array[i:i+18, j:j+9]
# 取得PM2.5的数值作为标签
label = array[i+9, j+9]
x_list.append(mat)
y_list.append(label)
x = np.array(x_list)
y = np.array(y_list)
return x, y, array
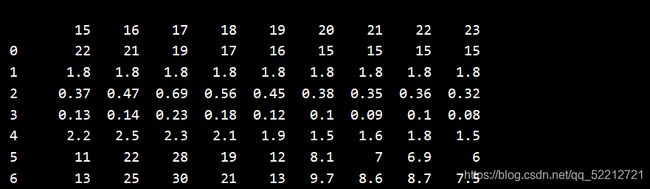
df:是pd.read_csv()函数读取train.csv获得的DataFrame格式的类表格结构。
其格式如下:
模型建立:
# 更新参数,训练模型
def train(x_train, y_train, epoch):
bias = 0 # 偏置值初始化
weights = np.ones(9) # 权重初始化
learning_rate = 1 # 初始学习率
reg_rate = 0.001 # 正则项系数
bg2_sum = 0 # 用于存放偏置值的梯度平方和
wg2_sum = np.zeros(9) # 用于存放权重的梯度平方和
for i in range(epoch):
b_g = 0
w_g = np.zeros(9)
# 在所有数据上计算Loss_label的梯度
for j in range(3200):
b_g += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-1)
for k in range(9):
w_g[k] += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-x_train[j, 9, k])
# 求平均
b_g /= 3200
w_g /= 3200
# 加上Loss_regularization在w上的梯度
for m in range(9):
w_g[m] += reg_rate * weights[m]
# adagrad
bg2_sum += b_g**2
wg2_sum += w_g**2
# 更新权重和偏置
bias -= learning_rate/bg2_sum**0.5 * b_g
weights -= learning_rate/wg2_sum**0.5 * w_g
# 每训练200轮,输出一次在训练集上的损失
if i%200 == 0:
loss = 0
for j in range(3200):
loss += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias)**2
print('after {} epochs, the loss on train data is:'.format(i), loss/3200)
return weights, bias
完整代码:
import pandas as pd
import numpy as np
# 数据预处理
def dataProcess(df):
#建立两个列表,跟数组类似,但当中存放的是索引
x_list, y_list = [], []
# df替换指定元素,将空数据填充为0
df = df.replace(['NR'], [0.0])
# astype() 转换array中元素数据类型
array = np.array(df).astype(float)
# 将数据集拆分为多个数据帧
#从0开始,到4320行,步长为18
for i in range(0, 4320, 18):
#从0列开始,到第15列结束
for j in range(15):
#获取一个二维列表,18行9列
mat = array[i:i+18, j:j+9]
# 取得PM2.5的数值作为标签
label = array[i+9, j+9]
x_list.append(mat)
y_list.append(label)
x = np.array(x_list)
y = np.array(y_list)
return x, y, array
# 更新参数,训练模型
def train(x_train, y_train, epoch):
bias = 0 # 偏置值初始化
weights = np.ones(9) # 权重初始化
learning_rate = 1 # 初始学习率
reg_rate = 0.001 # 正则项系数
bg2_sum = 0 # 用于存放偏置值的梯度平方和
wg2_sum = np.zeros(9) # 用于存放权重的梯度平方和
for i in range(epoch):
b_g = 0
w_g = np.zeros(9)
# 在所有数据上计算Loss_label的梯度
for j in range(3200):
b_g += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-1)
for k in range(9):
w_g[k] += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias) * (-x_train[j, 9, k])
# 求平均
b_g /= 3200
w_g /= 3200
# 加上Loss_regularization在w上的梯度
for m in range(9):
w_g[m] += reg_rate * weights[m]
# adagrad
bg2_sum += b_g**2
wg2_sum += w_g**2
# 更新权重和偏置
bias -= learning_rate/bg2_sum**0.5 * b_g
weights -= learning_rate/wg2_sum**0.5 * w_g
# 每训练200轮,输出一次在训练集上的损失
if i%200 == 0:
loss = 0
for j in range(3200):
loss += (y_train[j] - weights.dot(x_train[j, 9, :]) - bias)**2
print('after {} epochs, the loss on train data is:'.format(i), loss/3200)
return weights, bias
# 验证模型效果
def validate(x_val, y_val, weights, bias):
loss = 0
for i in range(400):
loss += (y_val[i] - weights.dot(x_val[i, 9, :]) - bias)**2
return loss / 400
def main():
# 从csv中读取有用的信息
# 由于大家获取数据集的渠道不同,所以数据集的编码格式可能不同
# 若读取失败,可在参数栏中加入encoding = 'gb18030'
df = pd.read_csv('train.csv', usecols=range(3,27),encoding ='GBK')
#print(df)
x, y, _ = dataProcess(df)
#划分训练集与验证集
x_train, y_train = x[0:3200], y[0:3200]
x_val, y_val = x[3200:3600], y[3200:3600]
epoch = 2000 # 训练轮数
# 开始训练
w, b = train(x_train, y_train, epoch)
# 在验证集上看效果
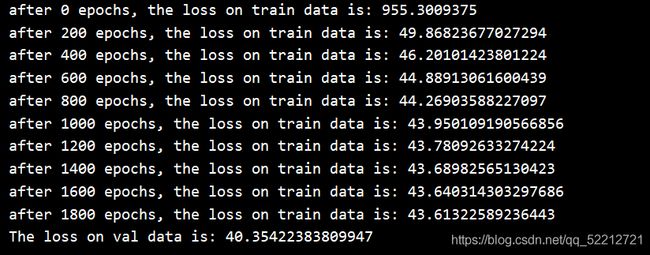
loss = validate(x_val, y_val, w, b)
print('The loss on val data is:', loss)
if __name__ == '__main__':
main()