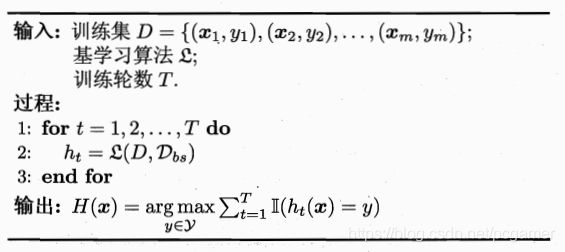机器学习读书笔记:集成学习
文章目录
- 集成学习
- AdaBoost
-
- 代码
- Bagging与随机森林
-
- Bagging
- 随机森林(Random Forest)
- 结合策略
- 增加多样性的策略
- 多样性度量
集成学习
之前已经讲过了好几个学习算法,或者说分类器、模型。都能达到一定的分类效果,俗话说的好:三个臭皮匠赛过诸葛亮。集成学习就是想将不同的学习算法集成在一起来工作,以期达到 1 + 1 ≥ 2 1+1\ge2 1+1≥2的效果。
个体学习期就是之前说过的各种各样的学习器:决策树、线性模型、支持向量机、贝叶斯分类器等。
- 如果所有的个体学习器都相同,这样的集成学习就是“同质”集成学习,个体学习器被称为“基学习器”或者“基学习算法”
- 如果所有的个体学习器不同,这样的集成学习就是“异质”集成学习,个体学习器就不被称为“基学习器”了。
从上面的图中可以看出,集成学习的重点部分就是在于各个个体徐诶器的结合策略。和足球队一样,大家要取长补短才能达到 1 + 1 ≥ 2 1+1\ge2 1+1≥2的效果。
比如下图中有三个个体学习器: h 1 , h 2 , h 3 h1, h2, h3 h1,h2,h3,如果结合策略采用最基本的“少数服从多数”的策略的话,根据不同的情况,同样的集成策略会有完全不同的效果。

另外还有一个问题就是,到底用多少个学习器会比较合适呢?《机器学习》上给出了一个数学推导。
- 假设每个基学习器(同质集成学习)的错误率是 ϵ \epsilon ϵ,也就是 P ( h i ( x ) ≠ f ( x ) ) = ϵ P(h_i(x)\neq f(x)) = \epsilon P(hi(x)=f(x))=ϵ
- 我们使用T个基学习器进行整合,通过简单的投票规则进行整合,以超过半数的结果为准。 那么集成的错误率就是:
P ( H ( x ) ≠ f ( x ) ) = ∑ k = 0 T / 2 ( T k ) ( 1 − ϵ ) k ϵ T − k ≤ e x p ( − 1 2 T ( 1 − 2 ϵ ) 2 ) P(H(x)\neq f(x))=\sum_{k=0}^{T/2}(\begin{matrix}T\\k\end{matrix})(1-\epsilon)^k\epsilon^{T-k} \\ \le exp(-\frac{1}{2}T(1-2\epsilon)^2) P(H(x)=f(x))=k=0∑T/2(Tk)(1−ϵ)kϵT−k≤exp(−21T(1−2ϵ)2)
从这个式子看出,如果T越大,错误率就会越低。
- 但是,这里的一个前提是所有的学习器都是相互独立的。而我们面对同一个问题而训练出来的学习器都是基于相同的数据,或者是通过某种划分策略选出来的训练样本,所以不可能是相互独立的。因此,直接增加基学习器的数量是无法直接达到提高准确率的。
学习器的集成方法一般分成两种:
- 串行的、强依赖的方式:AdaBoost
- 并行的、低依赖的方式:Bagging与随机森林
AdaBoost
书中的AdaBoost算法是基于同质集成学习来进行讨论的。
AdaBoost是基于以下的思路进行集成:
- 依次训练若干个(T个)基学习算法。
- 为训练集中的每个样本分配相应的权重,这些权重在每一次训练可以视作为一种分布 D D D。
- 在前一个学习器训练完之后,更新样本的权重,使得在第一次学习器中分类失败的样本权重升高,分类正确的样本的权重降低。
- 每个学习器也存在一个权重 α \alpha α,权重 α \alpha α会根据每次训练的错误率 ϵ \epsilon ϵ来进行计算。最终得到集成输出 H ( x ) = s i g n ( ∑ t = 1 T α t h t ( x ) ) H(x)=sign(\sum_{t=1}^T{\alpha_th_t(x)}) H(x)=sign(∑t=1Tαtht(x))。
书中给出了训练过程的伪代码:
这里解释下其中几行伪代码的来历:
-
第一行初始化权重,每个样本的权重均为1/m。
-
第四行是计算训练后学习器的错误率。
-
第五行是因为,如果训练错误率小于0.5,对于二分类问题比随机猜测还低,就不值得考虑了。语境中的弱学习器也是要高于0.5的正确率的。
-
第六行是根据错误率来计算当前学习器的权重的。从这个公式来看,错误率越低,相应的权重就会越大。为啥等于这个公式,我没怎么看懂就接受了这个结论,有兴趣的朋友可以去琢磨一下。
-
第7行是为下一次迭代计算样本权重。按照AdaBoost的思路,下一次的迭代在最好情况下应该可以修复掉前一轮的所有错误样本分类。这里解释一下东西:当 h t ( x ) = f ( x ) h_t(x)=f(x) ht(x)=f(x)时, h t ( x ) ∗ f ( x ) = 1 h_t(x)*f(x)=1 ht(x)∗f(x)=1,因为作为一个二分类问题, h ( x ) h(x) h(x)和 f ( x ) f(x) f(x)符号相同的话,肯定是等于1。所以,当 h t ( x ) ≠ f ( x ) h_t(x)\neq f(x) ht(x)=f(x)时, h t ( x ) f ( x ) = − 1 h_t(x)f(x)=-1 ht(x)f(x)=−1。所以根据第7行的公式,先不看 Z t Z_t Zt的话:
D t + 1 ( x ) = D t ( x ) ∗ e − α t , i f h t ( x ) = f ( x ) D t + 1 ( x ) = D t ( x ) ∗ e α t , i f h t ( x ) ≠ f ( x ) D_{t+1}(x)=D_t(x)*e^{-\alpha_t}, if h_t(x)=f(x) \\D_{t+1}(x)=D_t(x)*e^{\alpha_t}, if h_t(x)\neq f(x) Dt+1(x)=Dt(x)∗e−αt,ifht(x)=f(x)Dt+1(x)=Dt(x)∗eαt,ifht(x)=f(x)
接下来是 Z t Z_t Zt的问题,书中的解释是一个规范化因子,我不是很理解这个东西,结合《机器学习实战》里面的代码实现,我理解这个东西应该是一个归一化的东西, D t + 1 D_{t+1} Dt+1这个权重向量计算出来之后还是一个分布,也就是 ∑ i = 1 m D i = 1 \sum_{i=1}^mD_{i} = 1 ∑i=1mDi=1。所以我这里参考《机器学习实战》一书中的: Z t = ∑ D i = n m t i Z_t=\sum{D_{i=n}^m{ti}} Zt=∑Di=nmti同样,如果有兴趣得知这个推导过程的可以自行研究,我是没太看明白。
-
把所有的学习器训练完之后,输出还是采用 T T T个学习器对新样本都输出,针对每个学习器的输出来乘以权重 α i \alpha_i αi,求和后进行 s i g n sign sign函数输出。
-
标准的AdaBoost只适合二分类问题,如要处理其他问题则需要做一些改造。
代码
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
retArray = ones((shape(dataMatrix)[0],1))
if threshIneq == 'lt':
retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
else:
retArray[dataMatrix[:,dimen] > threshVal] = -1.0
return retArray
def buildStump(dataArr,classLabels,D):
dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
m,n = shape(dataMatrix)
numSteps = 10.0; bestStump = {
}; bestClasEst = mat(zeros((m,1)))
minError = inf #init error sum, to +infinity
for i in range(n):#loop over all dimensions
rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
stepSize = (rangeMax-rangeMin)/numSteps
for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
for inequal in ['lt', 'gt']: #go over less than and greater than
threshVal = (rangeMin + float(j) * stepSize)
predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
errArr = mat(ones((m,1)))
errArr[predictedVals == labelMat] = 0
weightedError = D.T*errArr #calc total error multiplied by D
#print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
if weightedError < minError:
minError = weightedError
bestClasEst = predictedVals.copy()
bestStump['dim'] = i
bestStump['thresh'] = threshVal
bestStump['ineq'] = inequal
return bestStump,minError,bestClasEst
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
weakClassArr = []
m = shape(dataArr)[0]
D = mat(ones((m,1))/m) #init D to all equal
aggClassEst = mat(zeros((m,1)))
for i in range(numIt):
bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
#print "D:",D.T
alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
bestStump['alpha'] = alpha
weakClassArr.append(bestStump) #store Stump Params in Array
#print "classEst: ",classEst.T
expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
D = multiply(D,exp(expon)) #Calc New D for next iteration
D = D/D.sum()
#calc training error of all classifiers, if this is 0 quit for loop early (use break)
aggClassEst += alpha*classEst
#print "aggClassEst: ",aggClassEst.T
aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
errorRate = aggErrors.sum()/m
print "total error: ",errorRate
if errorRate == 0.0: break
return weakClassArr,aggClassEst
def adaClassify(datToClass,classifierArr):
dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
m = shape(dataMatrix)[0]
aggClassEst = mat(zeros((m,1)))
for i in range(len(classifierArr)):
classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
classifierArr[i]['thresh'],\
classifierArr[i]['ineq'])#call stump classify
aggClassEst += classifierArr[i]['alpha']*classEst
print aggClassEst
return sign(aggClassEst)
Bagging与随机森林
Bagging
上面提到的AdaBoost是串行的进行训练,每个学习器都是使用全部的训练集样本数据。这样使得所有的学习器都没法“独立”。因此,Bagging是与AdaBoost不同的思路,是将所有的样本拆分成T份,用每份数据去训练T个学习器,从而降低学习器之间的关联关系。
将样本进行拆分的策略也不是简单的进行M/T的划分,而是采用前面介绍过的
进行划分来生成T份训练样本集。对T个学习器的决策输出也是采用基本的投票法(分类)或者简单平均法(回归)进行输出:
随机森林(Random Forest)
如果使用Bagging集成方法,而基学习器为决策树的话(
),再增加一点改造就是随机森林了。所以说随机森林是Bagging集成方法上的一个特殊变体。这点点改造就是指在决策树的基学习器训练过程中,每次创建节点选择最优属性进行划分时,引入一个随机变量 k k k。如果令 k = d k=d k=d,就是普通的决策树,而训练多个决策树后进行集成就是普通的Bagging方法。
如果令 k = 1 k=1 k=1,就是在随机选择一个。每个基学习器通过随机选择增加泛化能力。一般的策略是令 k = log 2 d k=\log_2d k=log2d。
结合策略
在对多个个体学习器进行结合输出的时候,这里就涉及到一个决策输出的策略问题,一般来说有如下几种:
-
平均法,一般用于回归问题。
- 简单平均法: H ( x ) = 1 T ∑ i = 1 T h i ( x ) H(x)=\frac{1}{T}\sum_{i=1}^T{h_i(x)} H(x)=T1∑i=1Thi(x)。
- 加权平均法: H ( x ) = 1 T ∑ i = 1 T w i h i ( x ) H(x)=\frac{1}{T}\sum_{i=1}^T{w_ih_i(x)} H(x)=T1∑i=1Twihi(x)
-
投票法,一般用于分类问题。
- 绝对多数投票法:若某类别超过半数,则预测为该类别。
- 相对多数投票法:预测类别为票数最多的那个类别。
- 加权投票法:为每个学习器给一个权值,然后再进行票数计数。
-
学习法,所有的个体学习器称为初级学习器,结合策略时也使用一个学习器,称之为次级学习器。使用初级学习器的输出样本来训练这个次级学习器,最终来做输出。
增加多样性的策略
开篇时讲到的,解决学习器之间的耦合性,让每个学习器尽量的“独立”,是提高集成学习的一个重要手段。
- 数据样本扰动:使用一些例如自助采样的不同的采样方法,对输入的样本数据进行一些挑选,来解决学习器之间的耦合性。
- 输入属性扰动:如果样本中的一些属性是冗余的,每个不同的学习器使用不同的属性集合进行训练。
- 输出表示扰动:手动修改一些标记。
- 算法参数扰动:也就是改一下算法模型的一些参数,增加一些随机变量进去。
多样性度量
那么怎么评价两个算法是否有耦合性呢?
首先列出两个算法之间的预测结果列联表:
h i , h j h_i, h_j hi,hj表示两个学习器,其中 a + b + c + d = m a+b+c+d=m a+b+c+d=m。
- 不合度量: d i s t i j = b + c m dist_{ij} = \frac{b+c}{m} distij=mb+c,也就是两个学习器不同的样本数有多少,值越大,多样性越大。
- 相关系数: ρ i j = a d − b c ( a + b ) ( a + c ) ( c + d ) ( b + d ) \rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}} ρij=(a+b)(a+c)(c+d)(b+d)ad−bc,如果值为0,则表示 h i , h j h_i,h_j hi,hj无关。
- Q-统计量: Q i j = a d − b c a d + b c Q_{ij}=\frac{ad-bc}{ad+bc} Qij=ad+bcad−bc。
- κ \kappa κ统计量: κ = p 1 − p 2 1 − p 2 \kappa=\frac{p1-p2}{1-p2} κ=1−p2p1−p2。其中 p 1 p1 p1为两个分类器取得一致的概率: p 1 = a + d m p1=\frac{a+d}{m} p1=ma+d, p 2 p2 p2为两个分类器偶然达成一致的概率,若两个分类器完全一致则 κ = 1 \kappa=1 κ=1,若只是偶然一致则 κ = 0 \kappa=0 κ=0。