【论文笔记】激光里程计网络 LO-Net:Deep Real-time Lidar Odometry2019
厦门大学,路易斯安那州立大学
本文提出了激光里程计LO-Net,其通过多任务学习对点云数据同时进行法向量估计、动态区域预测、相机位姿回归。
此外还设计了一个scan2map 的建图模块来降低累计误差、提升里程计的精度。
达到了超越DP-based方法、与几何结构方法SOTA–LOAM相似的里程计性能。
网络结构
网络输入为前后帧的点云数据,网络分为三个部分:
最后,还有一个将当前帧的点云注册到map中的建图模块,负责将预测的相对位姿根据map转换为绝对位姿然后输出。
点云数据encoding:
处于速度的考虑,作者选择将点云投影到圆柱平面上:
α = arctan ( y / x ) / Δ α β = arcsin ( z / x 2 + y 2 + z 2 ) / Δ β \begin{array}{l} \alpha=\arctan (y / x) / \Delta \alpha \\ \beta=\arcsin \left(z / \sqrt{x^{2}+y^{2}+z^{2}}\right) / \Delta \beta \end{array} α=arctan(y/x)/Δαβ=arcsin(z/x2+y2+z2)/Δβ
其中 Δ α Δ β \Delta \alpha \ \ \Delta \beta Δα Δβ分别是水平和垂直方向上连续光束发射器之间的平均角分辨率。
位于 ( α , β ) (\alpha,\beta) (α,β)处的像素包含距离信息: r = x 2 + y 2 + z 2 r=\sqrt{x^{2}+y^{2}+z^{2}} r=x2+y2+z2以及激光强度信息。
对于多个点同时对应到一个像素的情况,只保留距离激光雷达最近的点。
投影后得到的柱面图尺寸:H×W×C
几何一致性约束
论文将几何一致性约束分别加入到三个网络模块的损失函数中,提升了网络的预测精度。
1. 法向量估计
假设柱面投影函数为P,前后帧的相对位姿变换为 T t T^t Tt,那么可以根据t-1时刻的柱面投影图 X t − 1 α β X_{t-1}^{\alpha \beta} Xt−1αβ推出t时刻的柱面投影图 X t α β X_{t}^{\alpha \beta} Xtαβ:
X ^ t α β = P T t P − 1 X t − 1 α β \hat{X}_{t}^{\alpha \beta}=P T_{t} P^{-1} X_{t-1}^{\alpha \beta} X^tαβ=PTtP−1Xt−1αβ
为了衡量预测的柱面图 X t α β X_{t}^{\alpha \beta} Xtαβ与真实的点云南数据投影后的柱面图之间的差异,作者选择使用法向量相似度最为衡量依据。原因在于由于点云的稀疏性,前后帧的点云并非是一一对应的,因此直接衡量对应点之间的距离会导致很大的误差。而法向量可以反映道路的平滑表面和清晰的边缘。如果在map中只保留平滑平面上的点,那么在注册点云时其法向量应当是非常相近的。
传统的点云法向量估计可以采用PCA的方法,但是在网络传播时计算特征值非常慢,因此本文采用了一种巧妙的设计:
-
直接计算该点附近四个点分别到该点的向量的法向量,然后将求得的法向量平均,得到该点处的法向量,如图:

计算公式:
N ( X i ) = ∑ X k i , X i j ∈ P ( w i k ( X i k − X i ) × w i j ( X i j − X i ) ) \mathcal{N}\left(X^{i}\right)=\sum_{X^{i}_{k}, X^{i} j \in \mathcal{P}}\left(w_{i k}\left(X^{i_{k}}-X^{i}\right) \times w_{i j}\left(X^{i_{j}}-X^{i}\right)\right) N(Xi)=Xki,Xij∈P∑(wik(Xik−Xi)×wij(Xij−Xi))
根据法向量计算损失函数值:
L n = ∑ α β ∥ N ( X ^ t α β ) − N ( X t α β ) ∥ 1 ⋅ e ∣ ∇ r ( X ^ t α β ) ∣ \mathcal{L}_{n}=\sum_{\alpha \beta}\left\|\mathcal{N}\left(\hat{X}_{t}^{\alpha \beta}\right)-\mathcal{N}\left(X_{t}^{\alpha \beta}\right)\right\|_{1} \cdot e^{\left|\nabla r\left(\hat{X}_{t}^{\alpha \beta}\right)\right|} Ln=αβ∑∥∥∥N(X^tαβ)−N(Xtαβ)∥∥∥1⋅e∣∇r(X^tαβ)∣
第一项是同一柱面图像素格之间的法向量距离,第二项是权重,其表示深度r关于像素坐标的导数,也就是说边缘区域权重更大。
2. 里程计regression:
网络结构:先使用encoder对加入了法向量信息的点云数据进行编码,然后接4层卷积层和3层全连接层输出坐标和四元数位姿。
考虑到网络的参数量,将绝大部分卷积换成了fireConv层。
位姿损失函数借鉴了PoseNet2:
L o = L x ( S t − 1 ; S t ) exp ( − s x ) + s x + L q ( S t − 1 ; S t ) exp ( − s q ) + s q s x = 0.0 s q = − 2.5 \begin{aligned} \mathcal{L}_{o} &=\mathcal{L}_{x}\left(S_{t-1} ; S_{t}\right) \exp \left(-s_{x}\right)+s_{x} \\ &+\mathcal{L}_{q}\left(S_{t-1} ; S_{t}\right) \exp \left(-s_{q}\right)+s_{q} \end{aligned}\\ s_{x}=0.0 \quad s_{q}=-2.5 Lo=Lx(St−1;St)exp(−sx)+sx+Lq(St−1;St)exp(−sq)+sqsx=0.0sq=−2.5
其中 L x ( S t − 1 ; S t ) = ∥ x t − x ^ t ∥ l L q ( S t − 1 ; S t ) = ∥ q t − q ^ t ∥ q ^ t ∥ ∥ l \begin{aligned} \mathcal{L}_{x}\left(S_{t-1} ; S_{t}\right) &=\left\|x_{t}-\hat{x}_{t}\right\|_{l} \\ \mathcal{L}_{q}\left(S_{t-1} ; S_{t}\right) &=\left\|q_{t}-\frac{\hat{q}_{t}}{\left\|\hat{q}_{t}\right\|}\right\|_{l} \end{aligned} Lx(St−1;St)Lq(St−1;St)=∥xt−x^t∥l=∥∥∥∥qt−∥q^t∥q^t∥∥∥∥l
3.动态区域MASk预测:
这里主要是把属于动态物体的点云找出来,给一个属于[0,1]范围的较低的置信度 M ( X t α β ) M(X_t^{\alpha\beta}) M(Xtαβ),避免其影响里程计精度。mask预测网络采用了encoder-decoder的结构,encoder网络的权重与位姿回归网络encoder共享权重,decoder同样采用了FireDeconv层。
将该置信度应用到之前的法向量估计损失函数上:
L n = ∑ α β M ( X t α β ) ∥ N ( X ^ t α β ) − N ( X t α β ) ∥ 1 ⋅ e ∣ ∇ r ( X ^ t α β ) ∣ \mathcal{L}_{n}=\sum_{\alpha \beta} \mathcal{M}\left(X_{t}^{\alpha \beta}\right)\left\|\mathcal{N}\left(\hat{X}_{t}^{\alpha \beta}\right)-\mathcal{N}\left(X_{t}^{\alpha \beta}\right)\right\|_{1} \cdot e^{\left|\nabla r\left(\hat{X}_{t}^{\alpha \beta}\right)\right|} Ln=αβ∑M(Xtαβ)∥∥∥N(X^tαβ)−N(Xtαβ)∥∥∥1⋅e∣∇r(X^tαβ)∣
然而网络在训练过程中会偷懒将所有置信度置为0来达到最小损失,因此需要额外约束,作者使用了交叉熵:
L r = − ∑ α β log P ( M ( X t α β ) = 1 ) \mathcal{L}_{r}=-\sum_{\alpha \beta} \log P\left(\mathcal{M}\left(X_{t}^{\alpha \beta}\right)=1\right) Lr=−αβ∑logP(M(Xtαβ)=1)
注意置信度是没有label数据的,可以看出这里是默认了所有label为1(即静态区域)。
最后的损失函数:
L = L o + λ n L n + λ r L r \mathcal{L}=\mathcal{L}_{o}+\lambda_{n} \mathcal{L}_{n}+\lambda_{r} \mathcal{L}_{r} L=Lo+λnLn+λrLr
建图:scan2map 优化
为了减小累计误差,使用法向量和mask选择平滑区域、静态区域的点注册到map中,流程图:

图中操作符含义:
* :平滑性度量c
使用平滑卷积核K对每个点法向量进行卷积:
c = ∑ k = 1 3 ( K ∗ N k ) 2 c=\sum_{k=1}^{3}\left(K * \mathcal{N}_{k}\right)^{2} c=k=1∑3(K∗Nk)2
C最小的前 n C n_C nC个点则被认为是平滑区域的点,之后会被注册到map中去。
∏ \prod ∏:计算绝对位姿的初始估计值(之后还有refine):
M init = M t − 1 M t − 2 − 1 M t − 1 \mathbf{M}_{\text {init}}=\mathbf{M}_{t-1} \mathbf{M}_{t-2}^{-1} \mathbf{M}_{t-1} Minit=Mt−1Mt−2−1Mt−1
Ψ \Psi Ψ:利用相对位姿 T t T_t Tt的线性插值消除点云的运动失真:
然后使用绝对位姿的初始估计值将点云 S t S_t St转换到map中,为之后的点云精细配准做好准备。该步骤期望找到最优的绝对位姿变换:
M ^ o p t = arg min M ^ ∑ i ( ( M ^ ⋅ p i − m i ) ⋅ n i ) 2 \hat{\mathbf{M}}_{o p t}=\underset{\hat{\mathbf{M}}}{\arg \min } \sum_{i}\left(\left(\hat{\mathbf{M}} \cdot \boldsymbol{p}_{i}-\boldsymbol{m}_{i}\right) \cdot \boldsymbol{n}_{i}\right)^{2} M^opt=M^argmini∑((M^⋅pi−mi)⋅ni)2
注意这里只要求投影点到目标点的向量 M ^ ⋅ p i − m i \hat{\mathbf{M}} \cdot \boldsymbol{p}_{i}-\boldsymbol{m}_{i} M^⋅pi−mi沿着目标点处的法向量的投影最小即可,不要求两点完全重合。(map中的点都是平滑平面上的点,这样避免点云稀疏性带来的问题)
θ \theta θ:迭代配准。
进行固定数目的迭代后得到精细化的配准结果:
最终的绝对位姿变换:
M t = ∏ k = 1 n i t e r M ^ k M i n i t \mathbf{M}_{t}=\prod_{k=1}^{n_{i t e r}} \hat{\mathbf{M}}_{k} \mathbf{M}_{i n i t} Mt=k=1∏niterM^kMinit
Φ \Phi Φ: 通过对Mt-1和Mt之间的车辆运动进行线性插值,从当前点云St生成新的点云。
∑ , N \sum,N ∑,N: 删除旧数据,加入新数据,map只保留100个scan数据。
实验评估:
KItti上训练,Ford上测试。
里程计性能:
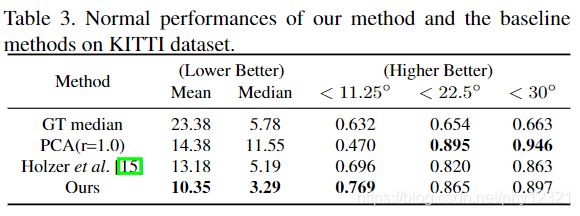
法向量预测结果评估:
使用PCA(r=0.1)计算的结果作为label
动态区域估计:
很好的区分了动态点云。
速度
veldyne激光雷达的扫描频率为10HZ,因此推理速度小于0.1s即可:

可以实时运行,时间主要花费在Mapping上。论文提到现有代码部分运行在CPU上,未来考虑全部运行在GPU上,以及可以使用多线程
待改进的问题
- 为了速度使用柱面图最为点云数据的表示形式,到那时三维视觉中直接使用点云更 practical
- 训练过程使用了真值,计划使用循环神经网络消除对真值数据的需求。