2020-01算法刷题集

2020-01算法刷题集

(0101)-(等差数列求项数)

(0103)-(最后四位数字)

(0105)-(排列)

(0107)-(特殊的标记)

(0109)-(数字处理)

(0111)-(特别数的和)

(0113)-(巨人排队)

(0115)-(漫漫上学路)

(0117)-(一二三)

(0119)-(真三国无双)

(0121)-(最小子集)

(0123)-(夫妻手牵手)

(0125)-(人民币转换)

(0127)-(不同的二叉查找树)

(0129)-(加油站)

(0131)-(会议室Ⅱ)

总结

---

• (0101)-(等差数列求项数)

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中N 个整数。
现在给出这N 个整数，小明想知道包含这N 个整数的最短的等差数列有几项？
【输入格式】
输入的第一行包含一个整数N。
第二行包含N 个整数A1,A2,...,ANA_{1}, A_{2}, ..., A_{N}A 

【输出格式】
输出一个整数表示答案。

【样例输入】
5
2 6 4 10 20

【样例输出】
10

【样例说明】
包含2、6、4、10、20 的最短的等差数列是2、4、6、8、10、12、14、16、18、20。

题目来源：第十届蓝桥杯-H题

解题过程：

没啥好讲的，因为马虎，导致错误理解题意，将最小项和次最小项作为数列的前两项。

最后发现数列的第二项可以不在输入样例中，所以需要使用控制变量，当an一定时，使得d尽可能地大，n才会小

需要使用辗转相除法求得最大公因数，另外，需要排序算法

代码(python实现)：

#author:zhj1121
#等差数列问题
def get_list():
    print("input:")
    num = eval(input(""))
    list_ele = input().split(' ')
    list1 = list(list_ele)
    intlist = []
    #list to int
    for i in list1:
        intlist.append(int(i))
    return intlist
def get_list_d(list):
    d = [''for i in range(len(list)-1)]
    for i in range(1,len(list)):
        d[i-1] = list [i]-list[i-1] 
    return d
def get_d(list):
    d = 10000
    for i in range(1,len(list)):
        a = list[i-1]
        b = list[i]
        if(a>=b):
            c = zzxcgetgys(a,b)
        else:
            c = zzxcgetgys(b,a)
        if(c

运行结果：

、

---

• (0103)-(最后四位数字)

给定数列1, 1, 1, 3, 5, 9, 17, …，从第4 项开始，每项都是前3 项的和。求
第20190324 项的最后4 位数字。

题目来源：第十届蓝桥杯-C题

解题过程：这道题就是斐波那契数列的变形，由于所求数值过大，所以不使用递归，直接迭代遍历

当然也有两个思路：

1.使用列表装载，但这道题没必要这样做，所以有第2种思路；

2.每一次迭代，只保存3个数，因为程序运行每一次运行就只是需要这三个数而已，没必要保存其它数据。

同样的道理，由于题目只要求出最后4位数字，所以可以同时将三位数求余，举个例子就可以知道是没有影响的

两种思路的代码分别如下

思路1：

#author:zhj1121
#time:0103
def fibonacci(n):
    fib = [i for i in range(n)]
    fib[0] = 1
    fib[1] = 1
    fib[2] = 1
    for i in range(3,n):
        fib[i] = (fib[i-1]+fib[i-2]+fib[i-3])%10000
    return fib[-1]
def main():
    num = fibonacci(20190324)
    print(num)
main()

思路2：

#author:zhj1121
#time:0103
def fibonacci2(n):
    a = 1
    b = 1
    c = 1
    for i in range(4,n+1):
        t = (a+b+c)%10000
        a = b
        b = c
        c = t
    return t
def main():
    t = fibonacci2(20190324)
    print(t)
main()

运行结果：

总结：通过这道题，可以明显地感受到通过修改算法可以提高程序运行速率，而且因题制宜，如果像之前的算法一样，使用递归，将会导致程序运行的时间非常地长。

• (0105)-(排列)

用1，3，5，8这几个数字，能组成的互不相同且无重复数字的三位数各是多少？ 总共有多少可能？

题目来源：第十届蓝桥杯-Python组-第1题

解题过程：这道题就是全排列问题，创建一个全排列函数生成所有的可能就可以了，需要i注意的是，这道题是4个数生成3个全排列，所有的可能和全排列可能是一样的，也是4*3*2=24种，至于结果，可以默认将最后一位不输出即可

代码如下：

#0105.py
#蓝桥杯python组第1题
per_result = []
def per(lst,s,e):
    if s == e:
        per_result.append(list(lst))
    else:
        for i in range(s,e):
            lst[i],lst[s] = lst[s],lst[i]#试探
            per(lst,s+1,e)#递归
            lst[i],lst[s] = lst[s],lst[i]
def main():
    lst = [1,3,5,8]
    per(lst,0,4)
    for i in per_result:
        for j in range(3):#只输出3个元素
            print(i[j],end="")
        print("")
    print(len(per_result))
main()

运行结果：

总结：由于放假回家，所以忙活了几天，这几天持续补更。

• (0107)-(特殊的标记)

编程实现：

打印出1-1000之间包含3的数字：

如果3是连在一起的(如33)则在数字前加上&；

如果这个数字是质数，则在数字后加上*，例:(3,13*，23*，&33，...，&233*...)

题目来源：第十届蓝桥杯-Python组-第2题

解题思路：

可以把这道题分为2步，3个“过滤器”，

把整个程序看成3个过滤器，对象是1-1000，

经过过滤器1：含有3的数，可以使用 字符串语法实现

将整数转换为字符串，如果字符3在字符串中，则符合过滤器要求，过滤出去

if('3' in str(num)):
    ...

将过滤器1获得的对象全部存储到一个列表中

创建两个函数：

如果经过过滤器2的数：含有 33 或者  333 的数，则返回 True

如果经过过滤器3的数：即质数(除1和自身不能被任何数整除)，则返回True

根据题意条件进行输出即可

代码如下：

#第十届蓝桥杯python组第2题
#test
#过滤器1
# num = 1222
# strnum = str(num)
# print('3' in strnum)
#过滤器2
# num = 1333
# if('33' in str(num) or '333' in str(num)):
#     num_str = str('&')+str(num)
#     print('&',end="")
#     print(num)
#过滤器3 简单写
def hasnum():
    lst_num = []
    for i in range(1,1001):
        num_str = str(i)
        if('3' in num_str):
            num_int = int(num_str)
            lst_num.append(num_int)
    return lst_num
# print(type(lst_result[0]))#success
def manynum(num):
    if('33' in str(num) or '333' in str(num)):
        return True
    else:
        return False
def isPrime(num):
    if(num==1):
        return False
    else:
        for i in range(2,num):
            if(num%i==0):
                return False
        return True
#print(isPrime(233))#success
def main():
    f_result_lst = hasnum()
    for i in f_result_lst:
        if(manynum(i) and isPrime(i)==False):
            print('&{}'.format(i))
        elif(manynum(i)==False and isPrime(i)):
            print('{}*'.format(i))
        elif(manynum(i) and isPrime(i)):
            print('&{}*'.format(i))
        else:
            print(i)
main()

运行结果(由于过长，只截部分)：

总结：在解题思路已完成总结

• (0109)-(数字处理)

让用户在一次输入时输入N个数字(2<=N<=15,即每次输入的数字数量不同)，数字之间以”,“作为分割

然后组合显示：

1.用户输入的数字个数

2.用户输入的最小的数字

3.将用户输入的数字按从大到小进行排列输出，数字之间以’,‘作为分割

4.如果用户输入的数字小于等于26，则找到相对应的26个大写英文字母(1 对应 ’A‘,26对应’Z‘，并拼接在一起打印显示

如果输入的数字在1-26之外，则不显示相应的字母。（例：程序输入214，则显示输出'[bad]').

输入：

N个数字，2<=N<=15

输出：

输入的数字个数

输入的最小数字

输入的数字从大到小排列

输入的数字所对应的字母

题目来源：第十届蓝桥杯-Python组-第3题

解题思路：没啥好说，当回顾基础吧

代码如下：

#第十届蓝桥杯-Python组-第3题)
#test
# print(chr(65))
def str_int(list):
    int_lst = [] 
    for i in list:
        int_lst.append(int(i))
    return int_lst
def main():
    lst = input().split(",")
    int_lst=str_int(lst)
#    print(int_lst)
    sort_lst = sorted(int_lst)
    #1
    print(len(sort_lst))
    #2
    print(sort_lst[0])
    #3
    sort_lst.reverse()
    for i in sort_lst:
        print(i,end=",")
    print("")
    #4
    for i in int_lst:
        if(i<=26):
            print(chr(64+i),end="")
        else:
            print("[bad]")
main()

运行结果：

• (0111)-(特别数的和)

标题：特别数的和

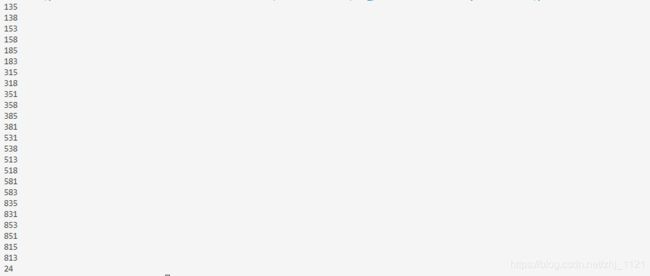
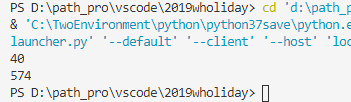
小明对数位中含有2,0,1,9的数字很感兴趣(不包括前导0)，在1到40中这样的数包括1，2，9，10至32，39，和40，共28个，他们的和是574.

请问，在1到n中，所有这样的数的和是多少？

输入格式：输入一行包含两个整数n

输出格式：输出一行，包含一个整数，表示满足条件的数的和

题目来源：第十届蓝桥杯-F题

解题思路：和 第十届蓝桥杯-Python组-第2题 类似

代码如下：

#(0111)-(第十届蓝桥杯-F题)
def add(list):
    sum = 0
    for i in list:
        sum +=i
    return sum
def main():
    sum = 0
    lst_result = []
    num = eval(input(""))
    for i in range(1,num+1):
        if('2' in str(i) or '0' in str(i) or '1' in str(i) or '9' in str(i)):
            lst_result.append(i)
    sum = add(lst_result)
    print(sum)
main()

运行结果：

• (0113)-(巨人排队)

巨人国的小学生放假了，老师要给小朋友们排队了。可是这个老师有强迫症，一定要队伍上的小朋友按照身高从高到矮排序（也就是排在前面的不能比后面的矮）。小朋友呢也很调皮，一旦老师给他排好队就不愿意动了。这个时候小朋友们一个一个的从教室里出来了，每个小朋友一出来老师就要给小朋友安排好位置。请问老师最少要给小朋友排几条路队呢？

输入：

两个数两行，第一行是人数(1<=n<=100000)，第二行的身高，身高不超过30000

输出：

最少队伍数

#0113-巨人排队
def findindex(list):
    for i in range(len(list)):
        if(list[i]==1):
            return i
    return -1
def trueorfalse(ele,list):
    tf_list = [0 for i in range(len(list))]
    for i in range(len(list)):
        if(list[i]>=ele):
            tf_list[i] = 1
    return tf_list
def main():
    num = eval(input())
    list_input = input().split(" ")
    int_list = []
    for i in list_input:
        int_list.append(int(i))
    #print(int_list)
    troops_list = []
    troops_list.append(int_list[0])
    for i in range(1,len(int_list)):
        tf_list = trueorfalse(int_list[i],troops_list)
        if(findindex(tf_list)==-1):
            troops_list.append(int_list[i])
        else:
            troops_list[findindex(tf_list)]=int_list[i]
    #print(troops_list)
    print(len(troops_list))
main()

题目来源：中南大学复试上机：1023: 巨人排队

解题思路：

—数据类型对象：

创建一个列表，为学生列表，用于存储教室中所有学生的身高，以遍历的方式模拟走出教室这一行为

创建一个列表，为矮列表，用于存储所有队伍中最矮学生的身高，即每只队伍的最后一名学生

—情景模拟(代码逻辑)：

从教室走出一个学生，这时有两种情况：

(遍历学生列表)

情况1：走出的学生比某只队伍中最矮学生的身高还矮或者相等,直接插入对应的队伍中

(情况1，将这个学生的身高替代矮列表对应的元素)

情况2：走出的学生比所有队伍中最矮学生的身高要高,这个学生自己站一只队伍

(情况2：将这个学生的身高直接插入矮列表中)

情景模拟如下：

运行结果：

补充(0116)

看了其它解法，都说需要贪心算法。但我觉得不需要贪心算法，因为贪心算法的前提就是需要对元素进行排序和贪心选择。

这个解法没用到并没有对元素进行排序，但是也正确的，例如以下描述：

因为其它解法都有一个共同点，就是尽量使相邻的学生的身高尽可能接近

所以可以将学生的身高数据时集中，时差距大

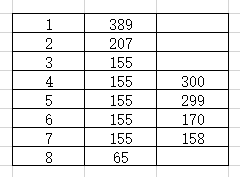
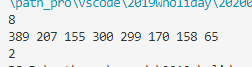
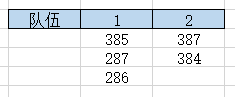
当教室的学生的顺序和身高如：385 287 387 286 384

—如果使用上述解法，也将会产生正确答案，即2支队伍

演算过程：

原因：因为整个程序演算过程已经将每支队伍的相邻学生的身高尽可能地接近，

当学生无法排在已产生的队伍时，将会独自产生一个队伍，

同时，前面队伍的最后一个学生的身高肯定比后面队伍的最后一个学生的身高要矮，

所以不必对每支队伍学生的身高进行排序操作

运行结果：

、

• (0115)-(漫漫上学路)

对于csuxushu来说，能够在CSU（California State University）上学是他一生的荣幸。CSU校园内的道路设计的十分精巧，由n+1条水平道路和n+1条竖直道路等距交错而成，充分体现了校园深厚的文化底蕴。然而不幸的是CS市每到夏季，天降大雨，使得CSU常常形成“CS海”的奇观，今年，也就是2016年同样也不例外，校园有一半的区域被淹了。
由于要进行一年一度激动人心的省赛选拔了，起迟了的csuxushu赶紧从寝室背着一包模板前往机房，好奇的csuxushu发现虽然道路被淹了，但是只有左上三角区域受到影响，也就是说他可以在副对角线以下的道路畅通行走。在这个惊人的场景下，csuxushu做了一个惊人的决定，他要算出他有多少种前往机房的最短路线。然而只有10分钟了，这时候他想到了你——全CSU最厉害的程序员来帮助他解决这个问题。
需要指出的是CSU可以看做左下顶点为csuxushu的寝室（0,0），右上顶点为机房（n,n）的方形区域。

输入：

多组数据。每组数据只有一行，为一个整数n（1 ≤n ≤30）。

输出：

每组数据输出一行，即由寝室到机房的最短路线方案数。测试数据保证结果为64位整数。

题目来源：中南大学ACM1772: 漫漫上学路

题目重读：

由于中南大学ACM题目的背景叙述过多，所以题目重读，如下：

副对角线：在代数学中，n阶行列式，从左上至右下的数归为主对角线，从左下至右上的数归为副对角线。

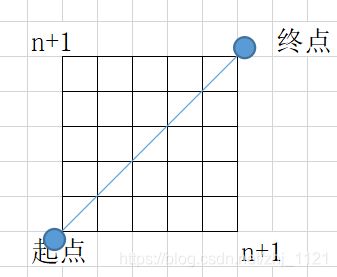
有一个人下图的左下角到右上角，有多少种路线？

解题思路：

可以知道这是卡特兰数，相关知识：卡特兰数-百度百科

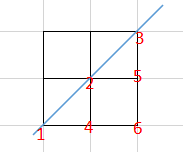
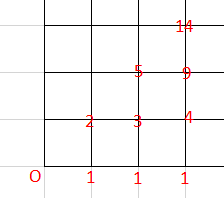
例如先假设输入1，就是2*2的格子

2*2 有2种可能：

1->4->2->5->3

1->4->6->5->3

3*3 有5种可能，在这里不进行叙述

所以这道题可以直接使用卡特兰数公式直接获得结果

程序代码：

#科特兰数
#0115
def Catalannumber(n):
    n+=1
    lst = []
    for i in range(n):
        lst.append([])
        for j in range(n):
            lst[i].append(1)
    for x in range(n):
        for y in range(n):
            if(x>y):
                lst[x][y] = 0
            elif(x==0 and y!=0):
                lst[x][y]=1
            elif(x!=0 and y==0):
                lst[x][y]=0
            elif(x==0 and y==0):
                lst[x][y]=0
            else:
                lst[x][y]=lst[x][y-1]+lst[x-1][y]
    return lst
#print(Catalannumber(4))
def main():
    num = eval(input("input:"))
    num = Catalannumber(num)[num][num]
    print("output:{}".format(num))
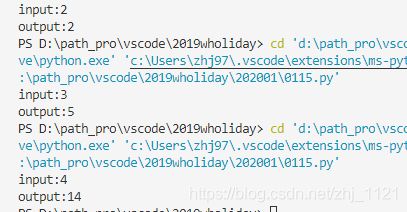
main()

运行结果：

• (0117)-(一二三)

你弟弟刚刚学会写英语的一(one)、二(two)和三(three)。他在纸上写了好些一二三，可惜有些字母写错了。已知每个单词最多有一个字母写错了（单词长度肯定不会错），你能认出他写的啥吗？

input:

第一行为单词的个数（不超过10）。以下每行为一个单词，单词长度正确，且最多有一个字母写错。所有字母都是小写的。

output:

对于每组测试数据，输出一行，即该单词的阿拉伯数字。输入保证只有一种理解方式。 

题目来源：中南大学ACM1110-一二三

(偷懒一天，最近有点忙，解道简单的题)

解题思路：直接暴力解题吧

首先进行单词长度的获取，再通过长度进行判断，如果长度是3，则是一或者二

如果长度大于3，则是三

再假设通过字符串的对比，进行判断

程序代码：

#0117
#一二三
def createone():
    one = []
    for i in range(26):
        ele1 = chr(97+i)+'ne'
        ele2 = 'o'+chr(97+i)+'e'
        ele3 = 'on'+chr(97+i)
        one.append(ele1)
        one.append(ele2)
        one.append(ele3)
    return one
def getnum(list):
    chinalist = []
    one = createone()
    for i in list:
        if(len(i)==3):
            if(i in one):
                chinalist.append('一')
            else:
                chinalist.append('二')
        else:
            chinalist.append('三')
    return chinalist
def main():
    num = eval(input())
    list = []
    for i in range(num):
        ele = input()
        list.append(ele)
    result = getnum(list)
    print(result)
main()

运行结果：

• (0119)-(真三国无双)

真三国无双是魔兽的一个游戏，该游戏是以中国三国的历史背景而制作的，该游戏是5 V 5的游戏模式，敌对双方各5个英雄，推掉了对方的大本营就算取得了胜利。

ZYH和SN都喜欢玩这个游戏，但是他们谁也不服谁，都觉得自己的操作比对方厉害，因此他们两人决定以单挑的方式来一决高下。ZYH选择了他最喜欢的英雄：关羽，SN也选择了他喜欢的英雄：典韦。

在他们开始正式比赛前，裁判介绍了一下关羽和典韦的技能。典韦有个脚踢地面而造成群晕的技能，简称为T，由于是游戏，它会有个动画效果，因此典韦使用T分为三个阶段：

点击T -> T的动画 -> T的释放

点击T的时间可以忽略，T的动画需要a(MS)；T的释放时间为b(MS)，在这段时间内，如果对方英雄在地面，就会被击晕。

而关羽使用技能D，过程是这样的：

点击D -> 选择方向 -> 转身（英雄会逆时针转身到选择的方向）-> 跳到空中-> 落下

点击D和选择方向的时间可以忽略，转身时间为c(MS)，跳到空中停留的时间为d(MS)。英雄当前方向与选择方向之间的逆时针夹角叫做旋转角度。转身时间c = 旋转角度 × 10 (MS)。在游戏中，旋转角度的范围为[0, 360)，不可能小于0或者大于等于360。

因此关羽和典韦单挑的时候，关羽喜欢用自己的技能D躲典韦的技能T，这就必须满足在典韦技能T释放的b(MS)时间内，关羽必须在空中。为了简化问题，我们认为，关羽在起跳或者落地的瞬间，典韦的技能T对他是无效的。

裁判正式介绍技能后，ZYH（关羽）就和SN（典韦）开始单挑了，他们在打架多次后，ZYH（关羽）和SN（典韦）的血量都处于死亡的边缘，此时SN（典韦）果断使用了自己的技能T，希望可以把ZYH（关羽）杀了，而ZYH（关羽）也在同时使用了技能D。

现在ZYH（关羽）求救于你，希望你能帮他计算关羽能选择的最小旋转角度，他的命就掌握在你的手上，你可不能随便应付吧。另外注意一点的就是，他们的技能现在只能释放一次。

input:

输入的第一行表示测试数据的组数N。

下面输入包括N行，每行包括三个整数，分别表示a, b, d (1 ≤ a ≤ 10000, 1 ≤ b ≤ 10000, 1 ≤ d ≤ 10000)。

output:

如果ZYH（关羽）可以成功躲掉SN（典韦）的技能T，则输出能成功躲避的最小旋转角度（小数点后保留两位有效数字）。否则输出IMPOSSIBLE；每个输出后都换一行。

题目来源：中南大学1020-真三国无双

题目重读：

有两个角色，典韦和关羽

典韦的技能T主要有两个阶段a+b,a表示技能动画，没有伤害，b表示技能，带有伤害

关羽的技能D主要有两个阶段c+d,

c表示转身的时间，可以受到伤害,而且时间与旋转的角度有关，c=角度*10；

d表示飞天，这段时间不受伤害

条件：

典韦和关羽同时使用技能，需要使关羽不受伤害

解题思路（好简单，直接考虑恒等就行）

程序代码

#0119.py
#真三国无双
def getdata():
    num = eval(input())
    list = []
    for i in range(num):
        ele = input().split(" ")
        list.append(ele)
    return list
def main():
    lst = getdata()
    for i in lst:
        if(i[1]>i[2]):
            print("IMPOSSIBLE")
        else:
            num = (int(i[0])-int(i[2])+int(i[1]))/10
            print("{:.2f}".format(num))
main()

运行结果：

• (0121)-(最小子集)

给一 非负 整数数组. 取数组中的一部分元素, 使得它们的和大于数组中其余元素的和, 求出满足条件的元素数量最小值.

题目来源：领扣761—最小子集

题目重读：

有几个关键字，非负、大于、其余、最小值

其中最小值即代表需要对数组进行降序排列，因为只有不断取出数组中的最大值，才能够满足最小这个条件；

其余则表示取数即是对原数组进行弹出操作，数组的状态是有所改变的

解题思路：

首相将数组中的数进行降序排列，再创建一个空的结果列表

不断弹出已排序好的数组的第一个元素，并存入结果列表中；

每一次弹出存入，都对数组的元素进行求和操作

当结果列表的元素和大于问题数组的元素和时，返回结果解表的长度，即是答案。

程序代码：

#lintcode-761-最小子集问题
#date:200121
#author:zhj1121
def getnums():
    str = input("").split(",")
    list_num = list(str)
    list_int = []
    for i in list_num:
        list_int.append(int(i))
    list_num = list_int
    return list_num
def getlistsum(list):
    sum = 0
    for i in list:
        sum+=i
    return sum
def getresult(list):
    list_result = []
    for i in range(len(list)):
        list_result.append(list.pop(0))
        if(getlistsum(list_result)>getlistsum(list)):
            return list_result
def main():
    list = getnums()
    list_sort = sorted(list)
    list_sort.reverse()
    list_result = getresult(list_sort)
    print(len(list_result))
main()

运行结果：

• (0123)-(夫妻手牵手)

N对夫妇坐在2N个排成一排的座位上. 现求最小的交换数量，使每对夫妇并坐一起，他们可以手牵着手。

一次交换可选择任何两个人交换座位。

人和座位由从0到2N-1的整数表示，夫妻按顺序编号，第一对是(0,1)，第二对是(2,3)，以此类推，最后一对是(2N-2,2N-1)。

初始座位由row [i]给出，表示坐在第i座位的人的编号。

示例1：

input

3，2，0，1 

output:

0

示例2：

input:

0，2，1，3

output：

1

题目来源：领扣LintCode—1043夫妻手牵手

题目重读：

这里提几个关键的词语和结论：

最大的数一定是奇数

当处理时，假定偶数是丈夫或者妻子都不会影响。

一个数只对应一个数，即一位丈夫对应一位妻子。且丈夫和妻子的位置谁在左谁在右都不会有影响

最少交换，即是不出现无效的交换，如果不规定最少，那么可以通过多次交换实现排序，最后也是满足条件的。

同时，如果每一次交换都有意义，那么就是最少交换

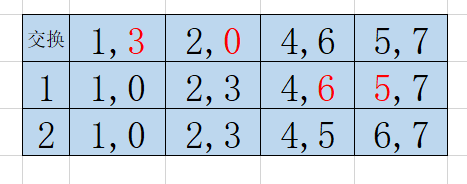
例如,4对夫妻：

可以发现，只要保证每一次交换都有意义，即每一次交换都要“成全”一对夫妻，那么就是最少交换。

解题思路：

将所有夫妇进行两两组合，不管是否是同一对夫妻。

对两两相邻的人进行判断，不仅对夫妇的编号，还对所处的位置进行处理。

例如[2,1,3,0]

这里假定偶数是丈夫，奇数是妻子，妻子的编号为丈夫的编号+1，这里默认0是偶数

拿编号为2来说，位置和编号都是偶数，该位置上是丈夫，所以需要找到对应的妻子，即3

丈夫在左边，妻子在右边

拿编号为1来说，位置和编号都是奇数，那么该位置上是妻子，所以需要找到对应的丈夫，即妻子的编号-1，即0

丈夫在左边，妻子在右边

拿编号为3来说，位置是偶数，编号是奇数，则该位置是妻子，所以需要找到对应的丈夫，即妻子的编号-1，即2

放置在这位妻子的右边 ，妻子在左边，丈夫在右边

拿编号为0来说，位置是奇数，编号是偶数，则该位置是丈夫，所以需要找到对应的妻子，即丈夫的编号+1，即1

放置在这位丈夫的左边，妻子在左边，丈夫在右边

这里需要注意位置关系，左右，因为只有这样，才能保证不会造成一对夫妇分别在这排座位的两侧。

另外，当从左到右交换完成后，完成交换的部分不能进行再次交换，保证满足最少交换的条件

程序代码：

#lintcode-1043-夫妻手牵手
#author:zhj1121
def getrole(num):
    if(num==0):
        return True
    else:
        if(num%2==0):
            return True
        else:
            return False
#找到一个数值i的位置list.index(x)
#交换列表i 和j的元素
def swap(i,j,list):
    intermediray = list[i]
    list[i] = list[j]
    list[j] = intermediray
def getdata():
    lst = input().split(",")
    str_lst = list(lst)
    int_lst = []
    for i in str_lst:
        int_lst.append(int(i))
    return int_lst
def seegroup(list):
    time = 0
    #[1,2,3,0]
    for i in range(len(list)-1):
        #[2,1,0,3]第一个元素2
        #最大的肯定不是偶数
        if(getrole(list[i]) and getrole(i)):
            if(list[i+1]!=list[i]+1):
                swap(i+1,list.index(list[i]+1),list)
                time+=1
        #[0,2,1,3]的第二个元素 2
        if(getrole(list[i]) and getrole(i)==False):
            if(list[i-1]!=list[i]+1):
                swap(i-1,list.index(list[i]+1),list)
                time+=1
        #[1,2,0,3]的第一个元素1
        if(getrole(list[i])==False and getrole(i)):
            if(list[i+1]!=list[i]-1):
                swap(i+1,list.index(list[i]-1),list)
                time+=1
        #[2,1,0,3]的第二个元素1,3
        if(getrole(list[i])==False and getrole(i)==False):
            if(list[i-1]!=list[i]-1):
                swap(i-1,list.index(list[i]-1),list)
                time+=1
    return time
def main():
    lst = getdata()
    time = seegroup(lst)
    print(time)
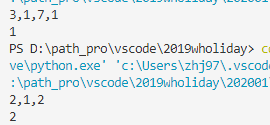
main()

运行结果：

• (0125)-(人民币转换)

描述：

将财务数字转换汉语中人民币的大写

input：

107000.53

output：

壹拾万柒仟元伍角叁分

题目来源：之前的一道算法作业题目，之前的代码量将近200多行，而且存在bug，所以重写

解题思路：（分治法）

首先对输入的金额，进行分离，分离小数点前后两部分。分开处理。

小数部分，有4种可能，见函数marklittlenum(num)

整数部分，以4个数字为一个整体，因为人民币金额就是这种模式，例如：

1234,5678,9123：

12个数字，有3部分，第一部分是9123，单位是元

第二部分是5678，单位是万

第三部分是1234，单位是亿

如果有第四部分，单位是万

当亿亿出现时，即是兆

所以处理好每一部分，4位数字，则处理好整体。

另外还有一些细节，不再赘述。

程序改进：有多处判断结构可以优化。另外，之前的多个金额出现bug，现在经过多次测试，暂时未发现存在的bug。

程序代码：

#name:人民币转换
author:zhj1121
date:200127
def textList(list):
    result = []
    str0 = "拾佰仟"
    str2 = "零壹贰叁肆伍陆柒捌玖"
    for i in list:
        if(len(i)==1):
            result.append(str2[int(i)])
        if(len(i)==2):
            result.append(str2[int(i[0])]+'拾'+str2[int(i[1])])
        if(len(i)==3):
            result.append(str2[int(i[0])]+'佰'+str2[int(i[1])]+'拾'+str2[int(i[1])])
        if(len(i)==4):
            result.append(str2[int(i[0])]+'仟'+str2[int(i[1])]+'佰'+str2[int(i[2])]+'拾'+str2[int(i[3])])
    return result
def split_num(num):
    num_str = str(num)
    len_num = len(num_str)
    data = []
    #如果长度是4的倍数
    if(len_num%4==0):
        total = int(len_num/4)
        for i in range(total):
            data.append(num_str[4*i:4*i+4])
    #如果长度不是4的倍数
    else:
        for i in range(4-len_num%4):
            num_str = '0'+num_str
        total = int(len(num_str)/4)
        for i in range(total):
            data.append(num_str[4*i:4*i+4])
    return data
def markzero(list):
    result =[]
    #处理单位左边为零的情况
    for i in list:
        #零仟零佰肆拾壹
        #list = ['零仟伍佰陆拾肆', '陆仟零佰捌拾柒', '陆仟伍佰零拾肆']
        #'零仟零佰零拾柒'
        if("零仟" in i or "零佰" in i or "零拾" in i):
            while("零仟" in i):
                i = i.replace("零仟","零")
            while("零佰" in i):
                i = i.replace("零佰","零")
            while("零拾" in i):
                i = i.replace("零拾","零")
            result.append(i)
        else:
            result.append(i)
    #处理2个零
    list = result
    result = []
    for i in list:
        while("零零" in i):
            i = i.replace("零零","零")
        while("拾零" in i):
            i = i.replace("拾零","拾")
        result.append(i)
    return result
def marklittlenum(num):
    str1 = str(num)
    list1 = list(str1)
    littlnum = []
    while("." in list1):
        littlnum.append(list1.pop(-1))
    while("." in littlnum):
        littlnum.pop(-1)
        littlnum.reverse()
    if(len(littlnum)!=0):
        int_list = []
        for i in littlnum:
            int_list.append(int(i))
        str2 = "零壹贰叁肆伍陆柒捌玖"
        if(len(int_list)>1):    
            if(int_list[0] ==0 and int_list[1] != 0):
                result_str = '零'+str2[int_list[1]]+'分'
            if(int_list[0] !=0 and int_list[1] != 0):
                result_str = str2[int_list[0]]+"角"+str2[int_list[1]]+"分"
        else:
            if(int_list[0] ==0):
                result_str = '整'
            else:
                result_str = str2[int_list[0]]+"角"
    else:
        result_str='整'
    return result_str
def main():
    num = eval(input())
    data_lst = split_num(int(num))
    lst = textList(data_lst)
    delzero = markzero(lst)
    list = ['元','万','亿','万']
    while(len(list)!=len(delzero)):
        list.pop(-1)
    list.reverse()
    result = []
    while(len(delzero)!=0):
        result.append(delzero.pop(0))
        result.append(list.pop(0))
    if(result[0][0]=="零"):
        result[0] = result[0][1:]
    if(result[-2][-1]=="零"):
        result[-2] = result[-2][:-1]
    for i in result:
        print(i,end="")
    print(marklittlenum(num))
main()

运行结果：

• (0127)-(不同的二叉查找树)

给出 n，问由 1...n 为节点组成的不同的二叉查找树有多少种？

input:

3

output:

5

解释：

题目来源：领扣LintCode163—不同的二叉查找树

解题思路：

卡特兰数的变形，所以可以像之前的走迷宫的一样，引用模板就可以了

程序代码：

def katelanshu(n):
    if(n==0):
        return 1
    else:
        n+=1
        lst = []
        for i in range(n):
            lst.append([])
            for j in range(n):
                lst[i].append(1)
        for x in range(n):
            for y in range(n):
                if(x>y):
                    lst[x][y] = 0
                elif(x==0 and y!=0):
                    lst[x][y]=1
                elif(x!=0 and y==0):
                    lst[x][y]=0
                elif(x==0 and y==0):
                    lst[x][y]=0
                else:
                    lst[x][y]=lst[x][y-1]+lst[x-1][y]
        n -=1
        return lst[n][n]
def main():
    num = eval(input())
    result = katelanshu(num)
    print(result)
main()

运行结果：

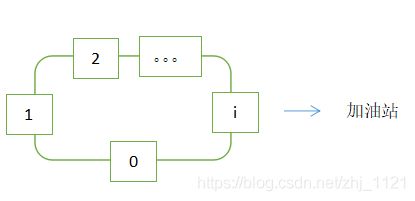
• (0129)-(加油站)

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油gas[i]，并且从第_i_个加油站前往第_i_+1个加油站需要消耗汽油cost[i]。

你有一辆油箱容量无限大的汽车，现在要从某一个加油站出发绕环路一周，一开始油箱为空。

求可环绕环路一周时出发的加油站的编号，若不存在环绕一周的方案，则返回-1。

（！注意：数据保证算法答案只有一个）

示例1：

input:

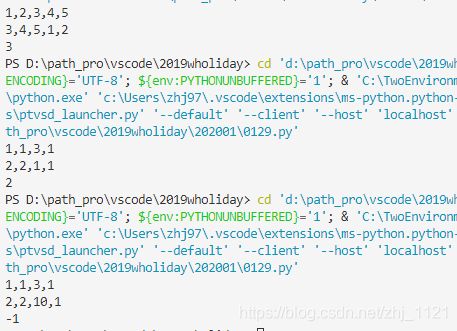
gas[i]=[1,1,3,1],cost[i]=[2,2,1,1]

output:

2

示例2：

input:

gas[i]=[1,1,3,1],cost[i]=[2,2,10,1]

output:

-1

题目来源：领扣LintCode—187加油站

解题思路：

题目有个地方需要注意，就是公路是环形公路，最后一站和第一站是相连的。即如下图：

另外，汽车是可以从任何一个站出发，但只有从其中的一个站出发，才能环路一周。

法1：

对所有的可能进行遍历，n个站，就有从n个站出发的可能。例如[0,1,2]

就有以下:[0,1,2]，[1,2,0],[2,0,1]种可能

再对每一种可能进行模拟，当出现costSum>gasSum时，则这种方案不可能

当某一种可能满足后，即弹出这种可能的出发的站点，即第0个元素

法2：

也是以上的解决方法，但拿到数据后，首先会每个加油站的油量以及到达下一个加油站的耗油量作差，当差值为负值时，即从该站出发时，连下一个加油站都无法到达，那么这种可能即被排除。

另外，将到达每个加油站的差值相加，当出现负值时，即代表无法到达下一个加油站，则进行排除。

当满足条件的可能出现时，弹出出发加油站的序号即可。

程序代码：

法1：（直接遍历查找所有的可能）

#0129.py
#加油站
def listSum(list):
    sum = 0
    for i in list:
        sum+=i
    return sum
def possResult(num):
    resultList = []
    numList = []
    count = 0 
    while(count<2):
        count+=1
        for i in range(num):
            numList.append(i)
    for x in range(num):
        lst = []
        for y in range(num):
            lst.append(numList[x+y])
        resultList.append(lst)
    return resultList
def getResult(gas,cost,possResult):
    if(listSum(cost)>listSum(gas)):
        return -1
    else:
        for i in possResult:
            gasSum = 0
            costSum = 0
            indexSum = 0
            for j in range(len(i)):
                indexSum +=gas[i[j]]
                if(gasSum>=costSum):
                    gasSum+=gas[i[j]]
                    costSum+=cost[i[j]]
                else:
                    break
            if(gasSum==indexSum):
                return i[0]
def main():
    gas  = []
    cost = []
    inputlst1 = input().split(",")
    for i in list(inputlst1):
        gas.append(int(i))
    inputlst2 = input().split(",")
    for i in list(inputlst2):
        cost.append(int(i))
    listlen = len(gas)
    possList = possResult(listlen)
    print(getResult(gas,cost,possList))
main()

法2：

#加油站
#date:200130
def takeSecond(elem):
    return elem[1]
def getdiffvalue(gas,cost):
    result = []
    for i in range(len(gas)):
        tuple = (i,gas[i]-cost[i])
        result.append(tuple)
    return result
def getPosResult(list):
    result = []
    for i in range(len(list)):
        if(list[i][1]>=0):
            result.append(list[i])
    return result
def possList(diffList,posList):
    numList = []
    lenList = len(diffList)
    count = 0 
    while(count<2):
        count+=1
        for i in range(lenList):
            numList.append(i)
    #return numList
    middList = []
    for x in range(lenList):
        lst = []
        for y in range(lenList):
            lst.append(numList[x+y])
        middList.append(lst)
    result = []
    for i in posList:
        lst = []
        for j in middList:
            if(j[0]==i[0]):
                result.append(j)
    return result
def run(possList,diffList):
    Listsum = 0
    for i in diffList:
        Listsum+=i[1]
    if(Listsum<0):
        return -1
    else:
        for i in possList:
            sum = 0
            indexsum = 0
            count = 0
            for j in i:
                indexsum += diffList[j][1]
                if(sum>=0):
                    sum += diffList[j][1]
                else:
                    break
            if(indexsum==sum):
                return i[0]
def main():
    gas  = []
    cost = []
    inputlst1 = input().split(",")
    for i in list(inputlst1):
        gas.append(int(i))
    inputlst2 = input().split(",")
    for i in list(inputlst2):
        cost.append(int(i))
    diffList = getdiffvalue(gas,cost)
    # print(diffList)
    sort_diffList= getdiffvalue(gas,cost)
    sort_diffList.sort(key=takeSecond,reverse=True)#每个加油站差值#排好序的
    #print(sort_diffList)
    posList = getPosResult(sort_diffList)#能出发的加油站
    #print(posList)
    possResult = possList(sort_diffList,posList)#几种可能
    #print(possResult)
    result = run(possResult,diffList)
    print(result)
main()

运行结果：

• (0131)-(会议室Ⅱ)

给定一系列的会议时间间隔intervals，包括起始和结束时间[[s1,e1],[s2,e2],...] (si < ei)，找到所需的最小的会议室数量。

input:

s[0]=0
e[0]=30

s[1]=5
e[1]=10

s[2]=15
e[2]=20

output:

2

解释：

需要两个会议室：会议室1:(0,30) ；会议室2:(5,10),(15,20)

题目来源：领扣LintCode—919会议室 II

解题思路：很像0113的巨人排队，以及之前的贪心算法解决活动安排问题。具体见上

区别在于：会议安排是所有的会议都记录在纸上的，所以是可以排序的。根据会议的开始时间进行升序排列

另外用一个会议室列表记录数值，该数值应该是会议的结束时间。进行比较时，应该是会议室列表的数值，即会议的结束时间和会议的开始时间

程序代码：

#0131—会议室2
def takeSecond(elem):
    return elem[0]
def findindex(list):
    for i in range(len(list)):
        if(list[i]==1):
            return i
    return -1
def trueorfalse(ele,list):
    tf_list = [0 for i in range(len(list))]
    for i in range(len(list)):
        if(list[i]<=ele):
            tf_list[i] = 1
    return tf_list
def meeting(meetList):
    roomList = []
    roomList.append(meetList[0][1])
    for i in range(1,len(meetList)):
        tf_list = trueorfalse(meetList[i][0],roomList)
        if(findindex(tf_list)==-1):
            roomList.append(meetList[i][1])
        else:
            roomList[findindex(tf_list)]=meetList[i][1]
    return roomList
def main():
    num = eval(input(""))
    meetList = []
    for i in range(num):
        input_start =eval(input("s["+str(i)+"]="))
        input_finish =eval(input("e["+str(i)+"]="))
        tuple = ()#purpose:def tuple to save the act_start and  act_finish
        tuple = (input_start,input_finish)
        meetList.append(tuple)
        del tuple
        print("")
    #meetList = [(0,30),(5,10),(15,20),(7,20),(2,3)]
    meetList.sort(key=takeSecond)#根据会议的开始时间进行排序
    roomList = meeting(meetList)
    print(len(roomList))
main()

运行结果：

• 总结

2020年的第一个月份，也是以月份为单位开始写算法刷题集的第一个月份。工作已经全部完成。之后可能会进行补充以及更新。

对于这套刷题集，怎么说呢，感觉完成得不尽如意。

首先，很多题目都是使用穷举法进行解答，列出所有可能，并对每一种可能进行排除，这样做虽然能得到正确的答案，但是却不是比较好的方式。

另外，有许多题目解决了，总结却写得不怎么好，以及一些题目的多种解法突然想到了，却没有记录下来。

不过，这一个月还是有所收获的。二月份会继续，但会设置为3天/篇，其实到中间的时候，就想要这样，但有始有终，定下的目标就得完成。从2月份开始，3天/篇，这样就可以进行总结和不会干涉其它的安排。