Graph Embedding
Graph Embedding
- DeepWalk:图网络与NLP的巧妙融合
-
- 先验知识
- Random Walk
- Skip-Gram
- DeepWalk
- LINE:不得不看的大规模信息网络嵌入
-
- 先验知识
- 一阶相似性的LINE模型
- 二阶相似性的LINE模型
- 模型优化与输出结果
因为莫名其妙的审稿意见(laji意见还拒稿了)就要开始学习Graph Embedding, 直接看论文看的一头雾水,所以来CSDN上搜集资料,从零开始学习Graph Embedding。
DeepWalk:图网络与NLP的巧妙融合
学习资料:DeepWalk:图网络与NLP的巧妙融合
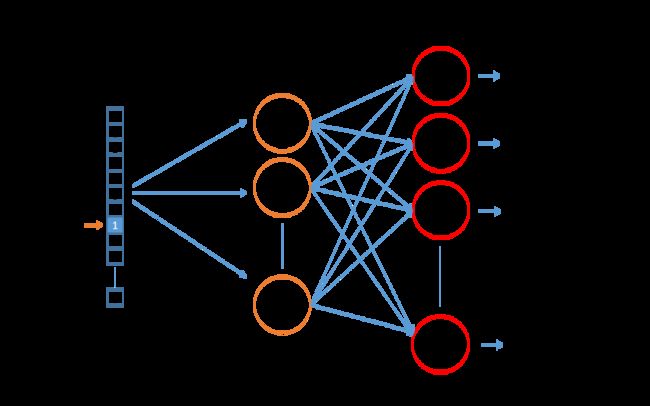
DeepWalk是首次将深度学习技术(无监督学习)引入到网络分析(network analysis)中的工作,它的输入是一个图,最终目标就是获得网络图中每个结点的向量表示 X e ∈ R ∣ V ∣ × d \mathbf{X}_{e} \in \mathbb{R}^{|V| \times d} Xe∈R∣V∣×d.
deepwalk给网络学习方向打开了一个新思路,有很多优点:
- 支持数据稀疏场景
- 支持大规模场景(并行化)
但是仍然存在许多不足:
- 游走是完全随机的,但其实是不符合真实的社交网络的;
- 未考虑有向图、带权图
先验知识
将network embedding的问题转化为word embeddin。转化的方式就是Random Walk ,通过这种方式将图结构表示为一个个序列,然后把这些序列当成一个个句子,每个序列中的结点就是句子中的单词。简单的说,DeepWalk = RandomWalk + SikpGram。

Random Walk
从输入图中的任意一个结点 v i v_{i} vi开始,随机选取与其邻接的下一个结点,直至达到给定长度 t t t, 生成的序列 W ~ v i = ( W v i 1 , ⋯ , W v i k , ⋯ , W v i t ) \tilde{\mathcal{W}}_{v_{i}}=\left(\mathcal{W}_{v_{i}}^{1}, \cdots, \mathcal{W}_{v_{i}}^{k}, \cdots, \mathcal{W}_{v_{i}}^{t}\right) W~vi=(Wvi1,⋯,Wvik,⋯,Wvit) 。对于每一个顶点 v i v_{i} vi, 都会随机游走出 γ \gamma γ 条序列。
采用随机游走有两个好处:
「利于并行化」:随机游走可以同时从不同的顶点开始采样,加快整个大图的处理速度;
「较强适应性」:可以适应网络局部的变化;
Skip-Gram
DeepWalk
deepwalk其实就是首先利用random walk来表示图结构,然后利用skip-gram模型来更新学习节点表示。算法流程如下所示:

算法有两层循环,第一层循环采样 γ \gamma γ 条路径,第二层循环遍历图中的所有结点随机采样一条路径并利用skip-gram模型进行参数更新。
其中第2步构建二叉树的目的是为了方便后续 SkipGram模型的层次softmax算法。
LINE:不得不看的大规模信息网络嵌入
学习资料:
- LINE:不得不看的大规模信息网络嵌入.
- 图嵌入-LINE-WWW-2015
论文来自2015年微软,
论文:LINE: Large-scale Information Network Embedding
链接:https://arxiv.org/abs/1503.03578
源码:https://github.com/tangjianpku/LINE
从论文标题就可以看出,文章主打大规模图网络。当时大多数的嵌入表示研究在小型图网络上表现非常不错,但是当网络规模扩展到百万、百亿级别时,就会显得不尽人意。此外,适用场景也比较有限,无法应用到有向或者带权重图中。为此,本文提出了一种新的网络向量嵌入模型LINE,以解决上述等问题。
先验知识
一阶相似性
一阶相似性定义为两个顶点 u u u 和 v v v 之间的邻近度,用该边的权重 W u v W_{u v} Wuv 表示,如果两个顶点之间没有边,那么它们的一阶相似性为0。这个概念是用于模型刻画局部信息的。
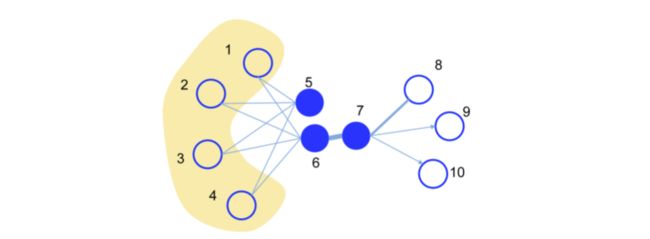
如上图,一阶相似性的大小就可以用链接线的粗细来表示。
二阶相似性
在真实场景中,大规模图中有链接的结点相对少,因此如果只用上述一阶相似性来建模是不全面的。比如上图中的5和6结点,两者没有链接,但是拥有几乎完全相同的邻居结点,我们可以认为它们的距离应该也是近的。二阶相似性定义为一对结点的邻居网络结构相似性。这个概念用于模型刻画全局信息。
KL散度 (KL-divergence)
KL散度是用于衡量两个概率分布相似性的指标,定义为:
D K L ( p ∥ q ) = ∑ i = 1 N p ( x i ) log p ( x i ) − ∑ i = 1 N p ( x i ) log q ( x i ) D_{K L}(p \| q)=\sum_{i=1}^{N} p\left(x_{i}\right) \log p\left(x_{i}\right)-\sum_{i=1}^{N} p\left(x_{i}\right) \log q\left(x_{i}\right) DKL(p∥q)=∑i=1Np(xi)logp(xi)−∑i=1Np(xi)logq(xi)
表示概率分布 p p p 和概率分布 q q q 之间的差异,越小越接近。其中 p p p 为真实分布, q q q 为近似 p p p 的分布。
一阶相似性的LINE模型
原空间:将边权归一化为概率
直观上两个结点的相似度是用链接强度表示,即边的权重,可以表示为,
p ^ 1 ( i , j ) = w i j W \hat{p}_{1}(i, j)=\frac{w_{i j}}{W} p^1(i,j)=Wwij
新空间:计算两点的共现概率
对于两个顶点 v i v_{i} vi 和 v j v_{j} vj ,它们之间的相似性可以用向量距离来表示(其中 u i u_{i} ui 和 u j u_{j} uj 分别表示对应的向量 )
p 1 ( v i , v j ) = 1 1 + exp ( − u ⃗ i T ⋅ u ⃗ j ) p_{1}\left(v_{i}, v_{j}\right)=\frac{1}{1+\exp \left(-\vec{u}_{i}^{T} \cdot \vec{u}_{j}\right)} p1(vi,vj)=1+exp(−uiT⋅uj)1
优化目标:两个空间中的概率分布保持一致
目标函数就是使得节点相似性 p 1 ( v i , v j ) p_{1}\left(v_{i}, v_{j}\right) p1(vi,vj) 和链接强度 p ^ 1 ( i , j ) \hat{p}_{1}(i, j) p^1(i,j) 尽可能地相同。论文里使用了上一节介绍的KL散度,本场景下,原空间的边概率分布 p ^ 1 ( i , j ) \hat{p}_{1}(i, j) p^1(i,j) 即真实分布 p p p ,新空间中的 p 1 ( v i , v j ) p_{1}\left(v_{i}, v_{j}\right) p1(vi,vj) 即近似分布 q q q.
O 1 = D K L ( p 1 ∥ p ^ 1 ) = ∑ ( i , j ) ∈ E p ^ 1 ( i , j ) log p ^ 1 ( i , j ) − ∑ ( i , j ) ∈ E p ^ 1 ( i , j ) log p 1 ( i , j ) O_{1}=D_{K L}\left(p_{1} \| \hat{p}_{1}\right)=\sum_{(i, j) \in E}\hat{p}_{1}(i, j) \log\hat{p}_{1}(i, j)-\sum_{(i, j) \in E} \hat{p}_{1}(i, j) \log {p}_{1}(i, j) O1=DKL(p1∥p^1)=∑(i,j)∈Ep^1(i,j)logp^1(i,j)−∑(i,j)∈Ep^1(i,j)logp1(i,j)
第一项为常数, W W W也是常数,省略所有常数后,目标函数如下:
O 1 = − ∑ ( i , j ) ∈ E w i j log p 1 ( v i , v j ) O_{1}=-\sum_{(i, j) \in E} w_{i j} \log p_{1}\left(v_{i}, v_{j}\right) O1=−∑(i,j)∈Ewijlogp1(vi,vj)
注意,一阶相似度仅适用于无向图。
二阶相似性的LINE模型
原空间:点的邻居边权归一化为概率
将从点 i i i 出发,指向的所有邻居的集合记为 N ( i ) \mathcal{N}(i) N(i) ,将相应的边集映射到一个概率空间中:记点 i i i 与它的邻居 j j j 之间的边权为 w i j w_{ij} wij,点 i i i 的出边的边权总和为 d i = ∑ j ∈ N ( i ) w i j d_{i}=\sum_{j \in \mathcal{N}(i)} w_{i j} di=∑j∈N(i)wij,出边 ( i , j ) (i, j) (i,j) 对应的边概率为:
p ^ 2 ( j ∣ i ) = w i j d i \hat p_{2}(j \mid i)=\frac{w_{i j}}{d_{i}} p^2(j∣i)=diwij
这个概率可以理解为当前节点是 i i i 的情况下,连接到它的邻居 j j j 的概率。
新空间:点的邻居内积归一化为概率
二阶相似性模型和word2vec类似,认为中间结点的上下文结点交集越大则越相似。对于每个节点 v i v_{i} vi 都有两个向量表示:一个是作为中间结点时的表示 u ⃗ i \vec{u}_{i} ui ,以及作为上下文结点时的表示 u ⃗ i ′ \vec{u}_{i}^{\prime} ui′ 。对于每一条边 ( i , j ) (i, j) (i,j) , 由结点 v ⃗ i \vec{v}_{i} vi 生成上下文 v ⃗ j \vec{v}_{j} vj 的概率为:
p 2 ( v j ∣ v i ) = exp ( u ⃗ j ′ T ⋅ u ⃗ i ) ∑ k = 1 ∣ V ∣ exp ( u ⃗ k ′ T ⋅ u ⃗ i ) p_{2}\left(v_{j} \mid v_{i}\right)=\frac{\exp \left(\vec{u}_{j}^{\prime T} \cdot \vec{u}_{i}\right)}{\sum_{k=1}^{|V|} \exp \left(\vec{u}_{k}^{\prime T} \cdot \vec{u}_{i}\right)} p2(vj∣vi)=∑k=1∣V∣exp(uk′T⋅ui)exp(uj′T⋅ui)
优化目标:两个空间中的概率分布保持一致
对于每个点,当它在原空间中的邻居概率分布和它在新空间的邻居概率分布趋于一致,便可认为原空间中的该点的二阶相似性被新空间保留下来。同一阶相似性,论文中定义了一个函数表示图上所有点的新旧空间概率分布差距和:
O 2 = ∑ i ∈ V λ i d ( p ^ 2 ( ⋅ ∣ v i ) , p 2 ( ⋅ ∣ v i ) ) O_{2}=\sum_{i \in V} \lambda_{i} d\left(\hat{p}_{2}\left(\cdot \mid v_{i}\right), p_{2}\left(\cdot \mid v_{i}\right)\right) O2=∑i∈Vλid(p^2(⋅∣vi),p2(⋅∣vi))
其中, λ i \lambda_{i} λi 表示点 i i i 在图中的重要性。论文中函数 d d d 采用了 KL 散度,推理同一阶相似性,最后得到
O 2 = − ∑ ( i , j ) ∈ E w i j log p 2 ( v j ∣ v i ) O_{2}=-\sum_{(i, j) \in E} w_{i j} \log p_{2}\left(v_{j} \mid v_{i}\right) O2=−∑(i,j)∈Ewijlogp2(vj∣vi)
注意,二阶相似度既可用于无向图,也可用于有向图、带权图。
模型优化与输出结果
二阶相似性的目标函数中, 与word2vec相同, p 2 ( v j ∣ v i ) p_{2}\left(v_{j} \mid v_{i}\right) p2(vj∣vi) 这一项的计算会涉及所有和结点 i i i 相邻结点的内积,计算量很大。为此作者采用了『负采样』的方式进行优化,其中第一项为正样本的边,第二项为采样的负样本边。
log σ ( u ⃗ j T ⋅ u ⃗ i ) + ∑ i = 1 K E v n ∼ P n ( v ) [ log σ ( − u ⃗ n ′ T ⋅ u ⃗ i ) ] \log \sigma\left(\vec{u}_{j}^{T} \cdot \vec{u}_{i}\right)+\sum_{i=1}^{K} E_{v_{n} \sim P_{n}(v)}\left[\log \sigma\left(-\vec{u}_{n}^{\prime T} \cdot \vec{u}_{i}\right)\right] logσ(ujT⋅ui)+∑i=1KEvn∼Pn(v)[logσ(−un′T⋅ui)]
然后,当模型在优化更新过程中,对结点embedding的计算如下,
∂ O 2 ∂ u ⃗ i = w i j ⋅ ∂ log p 2 ( v j ∣ v i ) ∂ u ⃗ i \frac{\partial O_{2}}{\partial \vec{u}_{i}}=w_{i j} \cdot \frac{\partial \log p_{2}\left(v_{j} \mid v_{i}\right)}{\partial \vec{u}_{i}} ∂ui∂O2=wij⋅∂ui∂logp2(vj∣vi)
很明显,当边的权重存在较大的方差时,会导致学习不稳定,无法选择一个合适的学习率。不难想到如果边的权重都相同,这个问题不就解决了。于是一个简单的做法是将权重为 w w w 的边拆分成 w w w 条binary edge,但是如果 w w w 很大则会很费存储空间。
一种更合理的思路是对边进行采样,采样概率正比于边的权重,然后把被采样到的边认为是binary edge处理。
通过优化一阶相似性和二阶相似性,可以得到顶点的两个表示向量,源向量和目标向量,在使用时,将两个向量结合起来作为顶点的最终表示。论文中说结合的方式是直接拼接。