【算法训练营学习笔记-Week05】动态规划其实“名不符实”,动态递推更容易理解...
不要对名字浮想联翩,过度扩充它的含义,我们更应该关注它的定义和它想表达的内容。
DP的关键就是求解子问题的时候,能够重复利用(reuse)已经求解的子问题结果,而不是从头计算,因此降低了计算的时间复杂度(但是提高了空间复杂度)。
Simplifying a complicated problem by breaking it down into simpler sub-problems.(in a recrusive manner)
DP两种形式
- 自顶向下(递归+记忆化)
- 自底向上(递推+状态表)
两种方法都是DP,但是为了提高DP能力,尽量将递归都转成递推。
动态规划和递归或者分治没有根本上的区别(关键看有无最优的子结构)
共性:找到重复子问题(计算机指令集)
差异性:最优子结构,中途可以淘汰次优解
做题的关键点
- 子问题,最优子结构
- 状态数组,存储中间状态(状态表, 可以是一维,或者是多维)
- 递推公式(状态转移方程或DP方程)
初学者/面试要关注于第二步,复杂题目关注第三步
复杂的递推无非两点:
- 维度增加(复杂题目,高维是常态)
- 存在取舍(最大值,最小值,有障碍等)
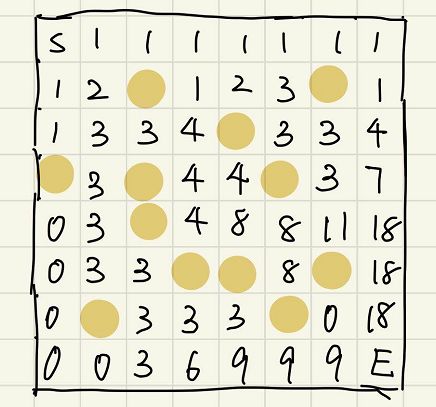
路径计数
题目
- 不同路径题目
- 不同路径 2 题目
子问题: 第i,j位置到end的走法=第i+1,j到end的走法 + 第i,j+1到终点的走法
状态定义:从当前点到end有多少走法
动态转移方程opt[i][j] =opt[i+1][j]+opt[i][j+1]
或者子问题可以定义为: 从start到i,j的走法 = 从start到i-1,j的走法 + 从start 到i,j-1的走法
状态定义: 从start开始到当前点有多少中走法,
DP方程opt[i][j] = opt[i-1][j] + opt[i][j-1]
实际写代码要注意状态表的初始化,例如斐波那契数列中的n=0,n=1情况。
class Solution {
public:
int uniquePathsWithObstacles(vector>& obstacleGrid) {
long int opt[100][100];
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
// 初始化第一行第一列
if (obstacleGrid[0][0] == 1 ){ //第一个位置就是障碍物,直接为0.
return 0;
} else{
opt[0][0] = 1;
}
for (int i = 1; i < m; i++){
opt[i][0] = obstacleGrid[i][0] == 1 ? 0 : opt[i-1][0];
}
for ( int j = 1; j < n; j++){
opt[0][j] = obstacleGrid[0][j] == 1 ? 0 :opt[0][j-1];
}
for ( int i = 1; i < m; i++){
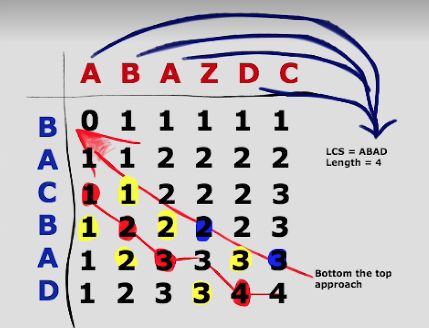
for ( int j = 1; j 最长公共子串(LCS)
题目
- 最长公共子序列题目
经验:字符串就需要扩展成二维的数组,也就是二维数组行和列分别对应两个字符串
子问题: 分为两种情况考虑
如果前一个字符串相同,LCS=两个字符串各减1后的LCS+1
如果前一个字符串不相同,LCS=S1字符串减1和S2的LCS 与 S1字符串和S2字符串-1的LCS 中的最大值
状态定义: 字符串S1前i个字符和字符串S2前j个字符的最长公共子串
状态转移方程
if S1[-1] != S2[-1]:
LCS[S1,S2] = max(LCS[S1-1,S2], LCS[S1,S2-1])
else:
LCS[S1,S2] = LCS[S1-1,S2-1] + 1
cpp代码如下
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
vector> opt(m+1, vector(n+1, 0)); // m+1 x n+1 的容器
for(int i = 1; i < m+1; i++){
for (int j = 1; j < n + 1; j++){
if (text1[i-1] == text2[j-1]){
opt[i][j] = opt[i-1][j-1] + 1;
} else{
opt[i][j] = max(opt[i-1][j], opt[i][j-1]);
}
}
}
return opt[m][n];
}
};
代码注意点:
- 数组的长/宽为字符串大小+1,所以初始化的第一行和第一列都是0
- 是比较
(text1[i-1] == text2[j-1]而不是比较(text1[i] == text2[j] - 注意数组不要越界
小结:
- 多练习,这类字符串题目是经验问题,只能多练习
- 数组大小,初始化,下标不能越界。
动态规划思维的小结
- 打破自己的思维惯性,形成机器思维(找重复性)
- 理解复杂逻辑的关键(树形结构)
- 也是职业进阶的要点要领(不需要亲力亲为,要放权,允许下属犯错)
补充内容: https://www.bilibili.com/video/av53233912, MIT算法课程
习题讲解
每次做DP题目之前,需要想到DP三个步骤:
- 寻找子问题
- 构建状态数组
- 定义DP方程
爬楼梯问题
https://leetcode-cn.com/problems/climbing-stairs/description/
过于简单: F(n) = F(n-1) + F(n-2)
思考题:
- 每次可以有1,2,3(简单)
- 每次依旧有1,2,3选择,但是相邻两步不能相同(中等)
三角形最小路径和
可能的方法,暴力递归(N层递归,每一层往左或者往右) 和 递归加记忆化
DP方法(O(mn ))
a. 重复性(子问题): problem(i,j) = min(sub(i+1,j), sub(i+1,j+1)) + a[i,j]
b. 定义状态数组 f[i,j]
c. DP方程 F[i,j] = min(F[i+1,j], F[i+1,j+1]) + a[i,j]
似乎只要定义成子问题,DP方程也就写出来了。
最大子序列和(高频)
最开始的思维方式是纯凭感觉,数学上不严谨,难以找到自相似性,具有拓展性,基本上无法使用代码实现。
a. 子问题:
定义子问题时候,根据经验,从后往前来看.
max_sum(i) = Max(max_sum(i-1) , 0) + a[i]
b. 状态数组定义
从一开始到第i个元素的累加后最大值。
c. DP方程
F[i] = Max(F[i-1], 0 +a[i])
或者,最大子序列和 = 当前元素自身最大,或者包含之前后最大
硬币兑换
解题方法
- 暴力递归
- BFS
- DP
这题,我把多种写法都写出来了, http://xuzhougeng.top/archives/leetcode-322-coin-changes
打家劫舍
参考之前斐波那契的思考题2
首先,我们定义数组 a[i] : 0..i ,第i天能偷到的最大金额 , 返回 a[n-1]
于是DP方程为 a[i] = a[i-1] + nums[i]
但是我们不确定第i-1的房子有没有被偷,缺少信息。
因此得到第一个经验,当你一维数组不够用的时候,就需要升维。比如说这里我们只用一维的话,永远不知道之前房子有没有被偷盗。
优化: 定义数组a[i][0,1] 1:不偷,0偷
- 如果不偷第i个房子,那么第i-1个房子可以偷,也可以不偷,选择其中的最大值
- 如果偷第i个房子,那么之前的房子一定不偷,当前房子肯定偷
于是新的DP方程
a[i][0] = Max(a[i-1][0], a[i-1][1])a[i][1]= a[i-1][0] + nums[i]
高级DP必经之路,增加维度。
继续优化: 新的状态定义 a[i]: 0..i 天,第i天必偷的最大值,返回max(a)
DP方程: a[i] = Max(a[i-1] + 0, a[i-2] + nums[i])
这个定义下,就类似于斐波那契数组了。
继续强调,面试的时候定义状态最重要,竞赛则是定义DP方程最难。
对于初学者,建议从第二维开始,进阶到只用一个维度。初学者要从工整的DP开始,不要一步登天。
其他
Cpp的二维数组定义
容器: m行n列的0
vector > vec( m, vector (n,0));
数组
//stack分配
int arr[m][n];
//heap分配
int **arr = new int*[m];//声明m行
for (int i = 0; i < m; i++){
arr[i] = new int[n]; //每个有n个元素
}
//删除
for (int i = 0; i < m; i++){
delete []arr[i];
}
delete [] arr;
数组求最大值和最小值(algorithm::max_element)
*max_element(dp, dp+m); //返回的是指针
在线的Cpp shell,http://cpp.sh/