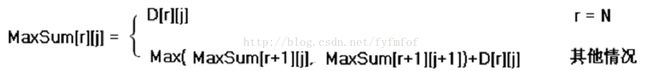【算法与实现】动态规划(基本思想)
动态规划(基本思想)
一、动归的基本思路
案例:数字三角形 POJ1163
在上面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。只需要求出这个最大和即可,不必给出具体路径。
思路:如果简单的用递归的方法来实现效率,在提交时会超时,应为不做任何处理的递归中进行了太多的重复计算,解决方法有2个,一个是记忆型递归,就是将递归中计算的值都用一个数组存起来再次计算就直接读取即可,如下:
#include
#include
using namespace std;
#define MAX 102
int num[MAX][MAX];
int MaxNum[MAX][MAX];
int n;
int maxNum(int i,int j)
{
if(MaxNum[i][j]!=-1)
returnMaxNum[i][j];
if(i==n)
return num[i][j];
MaxNum[i+1][j]=maxNum(i+1,j);
MaxNum[i+1][j+1]=maxNum(i+1,j+1);
if(MaxNum[i+1][j]>MaxNum[i+1][j+1])
return MaxNum[i+1][j]+num[i][j];
else
returnMaxNum[i+1][j+1]+num[i][j];
}
int main()
{
inti,j;
scanf("%d",&n);
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
{
scanf("%d",&num[i][j]);
MaxNum[i][j]=-1;
}
printf("%d\n",maxNum(1,1));
return 0;
} 还有一种就是用循环的方式进行递归,而且可以在空间上做到一定的优化,如下:
#include
#include
using namespace std;
#define MAX 101
int num[MAX][MAX];
int n;
int MaxNum[MAX];//使用一维数组循环递推
void maxNum()
{
inti,j;
for(j=1;j<=n;j++)
MaxNum[j]=num[n][j];
for(i=n;i>1;i--)
for(j=1;jMaxNum[j+1])
MaxNum[j]=MaxNum[j]+num[i-1][j];
else
MaxNum[j]=MaxNum[j+1]+num[i-1][j];
}
}
int main()
{
scanf("%d",&n);
inti,j;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
scanf("%d",&num[i][j]);
maxNum();
printf("%d\n",MaxNum[1]);
return 0;
} 以上面的例子可以列出来动态规划解题的一般思路,如下:
1. 将原问题分解为子问题
把原问题分解为若干个子问题,子问题和原问题形式相同或类似,只不过规模变小了。子问题都解决,原问题即解决(数字三角形例)。
子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
2. 确定状态
所有“状态”的集合,构成问题的“状态空间”。“状态空间”的大小,与用动态规划解决问题的时间复杂度直接相关。在数字三角形的例子里,一共有N×(N+1)/2个数字,所以这个问题的状态空间里一共就有N×(N+1)/2个状态。整个问题的时间复杂度是状态数目乘以计算每个状态所需时间。在数字三角形里每个“状态”只需要经过一次,且在每个状态上作计算所花的时间都是和N无关的常数。
用动态规划解题,经常碰到的情况是,K个整型变量能构成一个状态(如数字三角形中的行号和列号这两个变量构成“状态”)。如果这K个整型变量的取值范围分别是N1, N2, ……Nk,那么,我们就可以用一个K维的数组array[N1][N2]……[Nk]来存储各个状态的“值”。这个“值”未必就是一个整数或浮点数,可能是需要一个结构才能表示的,那么array就可以是一个结构数组。一个“状态”下的“值”通常会是一个或多个子问题的解。
3. 确定一些初始状态(边界状态)的值
以“数字三角形”为例,初始状态就是底边数字,值 就是底边数字值。
4. 确定状态转移方程
定义出什么是“状态”,以及在该 “状态”下的“值”后,就要找出不同的状态之间如何迁移――即如何从一个或多个“值”已知的“状态”,求出另一个“状态”的“值”(“人人为我”递推型)。状态的迁移可以用递推公式表示,此递推公式也可被称作“状态转移方
程”。
数字三角形的状态转移方程:
※能用动规解决的问题的特点:
1) 问题具有最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质。
2) 无后效性。当前的若干个状态值一旦确定,则此后过程的演变就只和这若干个状态的值有关,和之前是采取哪种手段或经过哪条路径演变到当前的这若干个状态,没有关系。
二、动归的三种基本形式
1)记忆递归型
优点:只经过有用的状态,没有浪费。递推型会查看一些没用的状态,有浪费
缺点:可能会因递归层数太深导致爆栈,函数调用带来额外时间开销。无法使用滚动数组节省空间。总体来说,比递推型慢。
案例:最长公共子序列 POJ1458
给出两个字符串,求出这样的一个最长的公共子序列的长度:子序列中的每个字符都能在两个原串中找到,而且每个字符的先后顺序和原串中的先后顺序一致。
记忆递归形式如下:
#include
#include
#include
using namespace std;
#define MAX 1000
char str1[MAX+2];
char str2[MAX+2];
int MaxLen[MAX+2][MAX+2];
int max(int x,int y)
{
if(x>y)
returnx;
else
returny;
}
int maxLen(int i,int j)
{
if(MaxLen[i][j]!=-1)
returnMaxLen[i][j];
if(i==0||j==0)
{
MaxLen[i][j]=0;
return0;
}
if(str1[i-1]==str2[j-1])
MaxLen[i][j]=maxLen(i-1,j-1)+1;
else
MaxLen[i][j]=max(maxLen(i-1,j),maxLen(i,j-1));
returnMaxLen[i][j];
}
int main()
{
inti,j,len1,len2;
while(scanf("%s%s",str1,str2)!=EOF)
{
len1=strlen(str1);
len2=strlen(str2);
for(i=0;i<=len1;++i)
for(j=0;j<=len2;++j)
MaxLen[i][j]=-1;
printf("%d\n",maxLen(len1,len2));
}
return0;
}
2)“我为人人”递推型
没有什么明显的优势,有时比较符合思考的习惯。个别特殊题目中会比“人人为我”型节省空间。
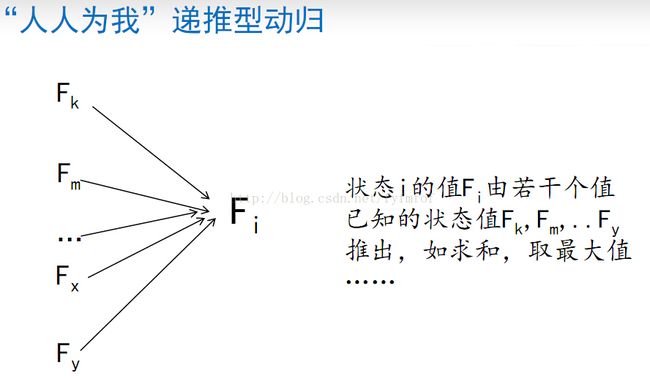
3)“人人为我”递推型
在选取最优备选状态的值Fm,Fn,…Fy时,有可能有好的算法或数据结构可以用来显著降低时间复杂度。
案例:最长上升子序列 百练2757
一个数的序列bi,当b1 < b2 < ... < bS的时候,我们称这个序列是上升的。对于给定的一个序列(a1, a2,..., aN),我们可以得到一些上升的子序列(ai1, ai2, ..., aiK),这里1 <= i1 < i2 < ... < iK <= N。比如,对于序列(1, 7, 3, 5, 9, 4, 8),有它的一些上升子序列,如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4,比如子序列(1, 3, 5, 8).你的任务,就是对于给定的序列,求出最长上升子序列的长度。
两种形式如下:
三、案例集锦&一些相关技巧
案例一:神奇的口袋 百练2755
有一个神奇的口袋,总的容积是40,用这个口袋可以变出一些物品,这些物品的总体积必须是40。John现在有n个想要得到的物品,每个物品的体积分别是a1,a2……an。John可以从这些物品中选择一些,如果选出的物体的总体积是40,那么利用这个神奇的口袋,John就可以得到这些物品。现在的问题是,John有多少种不同的选择物品的方式。
递归:
循环:
案例二:0-1背包问题 POJ3624
循环形式,代码如下:
#include
#include
using namespace std;
#define Max_N 3500
#define Max_M 13000
//Max_M太大,2维数组会超内存,记忆递归不能使用
int W[Max_N];
int D[Max_N];
int V[Max_M];
int m,n;
int max(int x,int y)
{
if(x>y)
returnx;
else
returny;
}
void maxV()
{
inti,j;
for(i=0;i=1;--j)//方向很重要
{
if(i==0)//初始化边界条件
{
if(W[i]>j)
V[j]=0;
else
V[j]=D[i];
}
elseif(j-W[i]>=0)
{//滚动循环递推
V[j]=max(V[j],V[j-W[i]]+D[i]);
}
}
}
int main()
{
inti;
scanf("%d%d",&n,&m);
for(i=0;i 案例三:滑雪 百练1088
Michael喜欢滑雪百这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上,这是最长的一条。
递归形式,代码如下:
#include
#include
#include
#include
using namespace std;
#define MAX 100
int H[MAX+2][MAX+2];
int MaxLen[MAX+2][MAX+2];
int r,c;
int max(int x,int y)
{
if(x>y)
returnx;
else
returny;
}
int maxLen(int i,int j)
{
if(MaxLen[i][j]!=-1)
returnMaxLen[i][j];
if(H[i][j]>H[i-1][j])
MaxLen[i][j]=max(MaxLen[i][j],maxLen(i-1,j)+1);
if(H[i][j]>H[i][j-1])
MaxLen[i][j]=max(MaxLen[i][j],maxLen(i,j-1)+1);
if(H[i][j]>H[i+1][j])
MaxLen[i][j]=max(MaxLen[i][j],maxLen(i+1,j)+1);
if(H[i][j]>H[i][j+1])
MaxLen[i][j]=max(MaxLen[i][j],maxLen(i,j+1)+1);
if(H[i][j]<=H[i-1][j]&&H[i][j]<=H[i][j-1]&&H[i][j]<=H[i+1][j]&&H[i][j]<=H[i][j+1])
MaxLen[i][j]=1;
returnMaxLen[i][j];
}
int main()
{
inti,j,MAX_L=-1;
scanf("%d%d",&r,&c);
for(i=0;i<=r+1;++i)
{
H[i][0]=INT_MAX;
H[i][c+1]=INT_MAX;
}
for(j=0;j<=c+1;++j)
{
H[0][j]=INT_MAX;
H[r+1][j]=INT_MAX;
}
for(i=1;i<=r;++i)
for(j=1;j<=c;++j)
{
scanf("%d",&H[i][j]);
MaxLen[i][j]=-1;
}
for(i=1;i<=r;++i)
for(j=1;j<=c;++j)
MAX_L=max(MAX_L,maxLen(i,j));
printf("%d\n",MAX_L);
return 0;
}
//如果用循环递推的话需要按照高度的顺序排列进行操作 案例四:一个美妙的栅栏 POJ1037
这里用到了计数的技巧+循环动归,代码如下:
#include
#include
#include
using namespace std;
#define MAX 20
#define DOWN 0
#define UP 1
__int64 C[MAX+2][MAX+2][2];
int seq[MAX+2];
bool used[MAX+2];
//C[i][j][DOWN]表示i根木棒中第j小打头的DOWN方案数
void init(int n)
{
inti,j,k;
memset(C,0,sizeof(C));
C[1][1][DOWN]=C[1][1][UP]=1;
for(i=2;i<=n;++i)
for(j=1;j<=i;++j)
{
for(k=1;kseq[i-1]))
skipped+=C[n-i+1][No][DOWN];
elseif(seq[i-1]>k&&(i<=2||seq[i-2]=x)
break;
}
}
used[k]=true;
seq[i]=k;
skipped=oldVal;
}
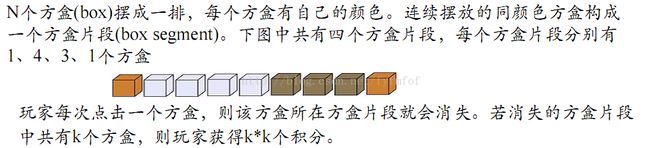
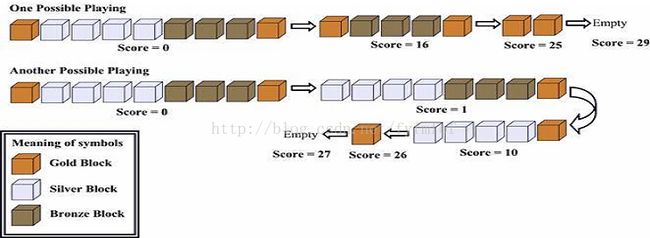
for(i=1;i 案例五:方盒游戏 POJ1390
求可以获得的最高分,代码如下:
#include
#include
#include
using namespace std;
struct box_segment
{
intcolor;
intlen;
};
struct box_segment segment[200];
int score[200][200][200];
int click_box(int start, int end, int extra_len)
{
inti, result, temp;
if( score[start][end][extra_len]>0 )
returnscore[start][end][extra_len];
result= segment[end].len+ extra_len;
result= result*result;
if(start==end)//递归边界
{
score[start][end][extra_len]=result;
returnscore[start][end][extra_len];
}
result+= click_box(start, end-1, 0);
i= end - 1;
for( i = end - 1; i >= start; i-- )
{
if(segment[i].color!=segment[end].color) continue;
//递推关系式
temp= click_box(start, i, segment[end].len+ extra_len) + click_box(i+1, end-1, 0);
if( temp<=result ) continue;
result= temp;
break;
}
score[start][end][extra_len]= result;
returnscore[start][end][extra_len];
}
int main()
{
intt, n, i, j, end, color;
scanf("%d",&t);
for(i=0;i 四、小结
动态规划的关键点在于找到最优子结构和列出状态转移方程,而且题目中很多时候会伴随着大量其他的解题技巧,所以如果要做好这一类题目就需要大量的练习作为经验,这次作为基本思想的总结就先列举这么多,之后估计还会加补充篇进行扩充。
注:以上总结部分类容来自于北京大学ACM暑期课程资料,总结只是为了方便自己查阅&和大家交流=.=
本文固定连接:http://blog.csdn.net/fyfmfof/article/details/41606781