机器学习实战13-卷积神经网络
机器学习实战13-设备和服务器上的分布式 TensorFlow就先不学习了，详情可参见：
十二、设备和服务器上的分布式 TensorFlow
卷积神经网络（CNN）是从大脑视觉皮层的研究中出现的，自 20 世纪 80 年代以来它们一直用于图像识别。在过去的几年里，由于计算能力的增加，可用训练数据的数量以及第 11 章介绍的训练深度网络的技巧，CNN 致力于在某些复杂的视觉任务中做出超出人类的表现。他们使图像搜索服务，自动驾驶汽车，视频自动分类系统等变得强大。此外，CNN 并不局限于视觉感知：它们在其他任务中也很成功，如语音识别或自然语言处理（NLP）; 然而，我们现在将专注于视觉应用。
视觉皮层的结构
视觉皮层中的许多神经元有一个小的局部感受野，这意味着它们只对位于视野中有限的一部分区域的视觉刺激起作用（见图，五个神经元的局部感受野由虚线圆圈表示）。不同神经元的感受野可能重叠，并且它们一起平铺了整个视野。此外研究表明，一些神经元只对水平线方向的图像作出反应，而另一些神经元只对不同方向的线作出反应（两个神经元可能具有相同的感受野，但对不同方向的线作出反应）。还注意到一些神经元具有较大的感受野，并且它们对较复杂的模式作出反应，这些模式是较低层模式的组合。这些观察结果让我们想到：更高级别的神经元是基于相邻低级神经元的输出（请注意，每个神经元只与来自前一层的少数神经元相连）。这个强大的结构能够检测视野中任何区域的各种复杂图案。
这些对视觉皮层的研究启发了 1980 年推出的新认知机（neocognitron），后者逐渐演变为我们现在称之为卷积神经网络。一个重要的里程碑是 Yann LeCun，LéonBottou，Yoshua Bengio 和 Patrick Haffner 于 1998 年发表的一篇论文，该论文引入了着名的 LeNet-5 架构，广泛用于识别手写支票号码。这个架构有一些你已经知道的构建块，比如完全连接层和 Sigmoid 激活函数，但是它还引入了两个新的构建块：卷积层和池化层。
卷积层
CNN 最重要的组成部分是卷积层：第一卷积层中的神经元不是连接到输入图像中的每一个像素（就像它们在前面的章节中那样，全连接），而是仅仅连接到它们的局部感受野中的像素（参见下图）。 进而，第二卷积层中的每个神经元只与位于第一层中的小矩形内的神经元连接。 这种架构允许网络专注于第一隐藏层中的低级特征，然后将其组装成下一隐藏层中的高级特征，等等。 这种层次结构在现实世界的图像中是很常见的，这也是 CNN 在图像识别方面效果很好的原因之一。
到目前为止，我们所看到的所有多层神经网络都有由一长串神经元组成的层，在输入到神经网络之前我们必须将输入图像压缩成 1D。 现在，每个图层都以 2D 表示，这使得神经元与其相应的输入进行匹配变得更加容易。
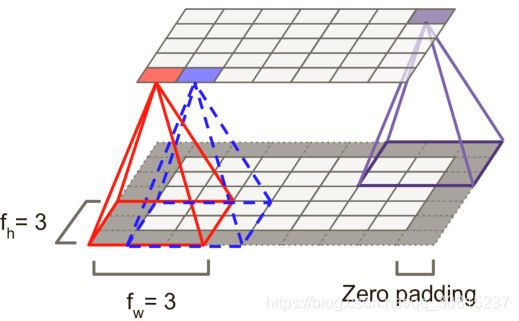
位于给定层的第i行第j列的神经元连接到位于前一层中的神经元的输出的第i行到第
行，第j列到第 
列。fh和fw是局部感受野的高度和宽度（见下图）。 为了使图层具有与前一图层相同的高度和宽度，通常在输入周围添加零，如图所示。 这被称为零填充Zero Padding。
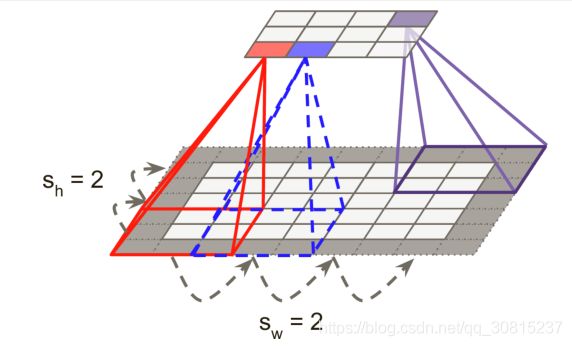
如下图所示，通过将局部感受野隔开，还可以将较大的输入层连接到更小的层。 两个连续的感受野之间的距离被称为步幅。 在图中，一个5×7的输入层（加零填充）连接到一个3×4层，使用3×3的卷积核和一个步幅为 2（步幅在两个方向是相同的，但是它并不一定总是如此）。 位于上层第i行第j列的神经元与位于前一层中的神经元的输出连接的第
至 
行，第
列， Sh和Sw是垂直和水平的步幅。
卷积核/过滤器
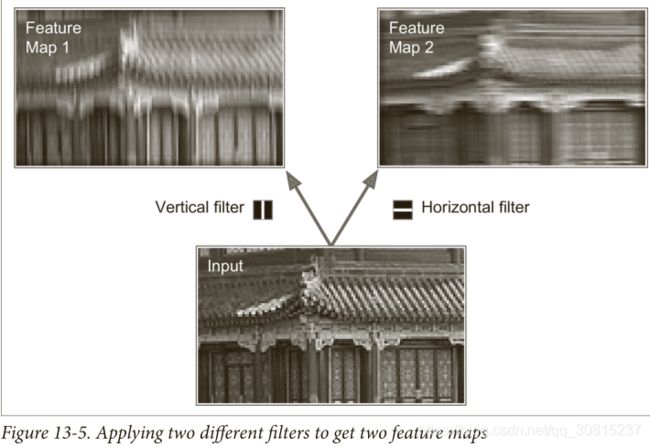
神经元的权重可以表示为局部感受野大小的小图像。 例如，图 13-5 显示了两个可能的权重集，称为过滤器（或卷积核）。第一个表示为中间有一条垂直的白线的黑色正方形（除了中间一列外，这是一个充满 0 的7×7矩阵，除了中央垂直线是 1）。 使用这些权重的神经元会忽略除了中央垂直线以外感受野的一切（因为除位于中央垂直线以外，所有的输入都将乘 0）。第二个卷积核是一个黑色的正方形，中间有一条水平的白线。 再一次，使用这些权重的神经元将忽略除了中心水平线之外的局部感受野中的一切。
现在，如果一个图层中的所有神经元都使用相同的垂直线卷积核（以及相同的偏置项），并且将网络输入到图 13-5（底部图像）中所示的输入图像，则该图层将输出左上图像。 请注意，垂直的白线得到增强，其余的变得模糊。 类似地，如果所有的神经元都使用水平线卷积核，右上角的图像就是你所得到的。 注意到水平的白线得到增强，其余的则被模糊了。因此，使用相同卷积核的一个充满神经元的图层将为您提供一个特征映射，该特征映射突出显示图像中与卷积核最相似的区域。 在训练过程中，CNN 为其任务找到最有用的卷积核，并学习将它们组合成更复杂的模式（例如，交叉是图像中垂直卷积和和水平卷积和都激活的区域）。
叠加的多个特征映射
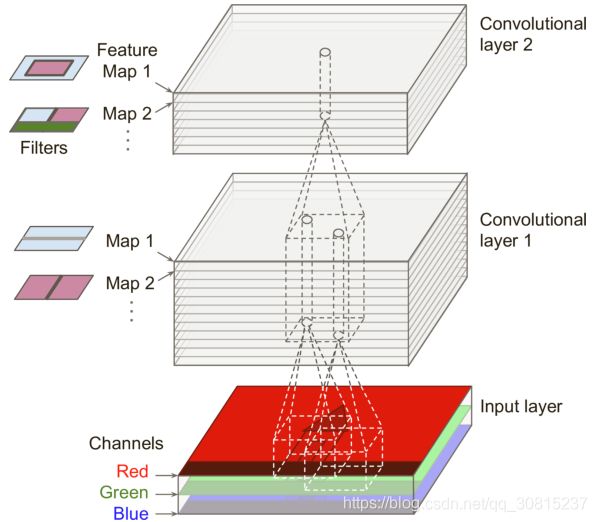
到目前为止，为了简单起见，我们将每个卷积层表示为一个薄的二维层，但是实际上它是由几个相同大小的特征映射组成的，所以使用3D图表示其会更加准确（见下图）。 在一个特征映射中，所有神经元共享相同的参数（权重和偏置，权值共享）（同一网络层的卷积核都相同，称为“权值共享”，能够有效减少网络参数），但是不同的特征映射可能具有不同的参数。 神经元的感受野与前面描述的相同，但是它延伸到所有先前的层的特征映射，即卷积层2的feature的输出是由卷积层1中所有featuremap 与一个卷积核的加权和。 简而言之，卷积层同时对其输入应用多个卷积核，使其能够检测输入中的多种特征。
事实上，特征图Feature Map中的所有神经元共享相同的参数会显着减少模型中的参数数量，但最重要的是，一旦 CNN 学会识别一个位置的模式，就可以在任何其他位置识别它。 相比之下，一旦一个常规 DNN 学会识别一个位置的模式，它只能在该特定位置识别它。
输入图像也由多个子图层组成：每个颜色通道一个。 通常有三种：红色，绿色和蓝色（RGB）。 灰度图像只有一个通道，但是一些图像可能更多。具体地，位于给定卷积层L中的特征映射k的i行，j列中的神经元连接到前一层（L-1）位于
行，
列的神经元的输出。
注意，位于同一行第i列和第j列但位于不同特征映射中的所有神经元都连接到上一层中完全相同神经元的输出。公式总结前面解释的数学公式：它展示了如何计算卷积层中给定神经元的输出。它是计算所有投入的加权总并且加上偏置。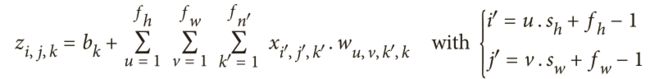 
-
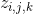是卷积层（L层）特征映射k中位于第i行第j列的神经元的输出. -
和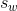 
是垂直和水平的步幅，
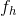和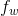 
是感受野的高度和宽度，
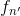是前一层（第L- 1层）的特征映射的数量。 -
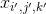是位于L-1层，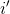
-
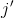
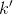
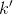
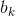是特征映射k的偏置项（在L层中）。您可以将其视为调整特征映射k的整体亮度的旋钮。 -
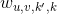是层L的特征映射k中的任何神经元与位于行u，列v（相对于神经元的感受野）的输入之间的连接权重，以及特征映射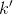
TensorFlow 实现
在 Tensorflow 中，每个输入图像的通常被表示为三维张量[height,width,channels] .。 一个小批次被表示为
四维张量 [mini-batchsize,height,width,channels]。 卷积层的权重被表示为四维张量
，分别代表高，宽，通道数(输入)，卷积核个数（输出）。 卷积层的偏差项简单地表示为一维形状的张量 
。
我们来看一个简单的例子。 下面的代码使用 Scikit-Learn 的load_sample_images()（一个中国庙宇，一朵花）加载两个样本图像。 然后创建两个7×7的卷积核（一个中间是垂直的白线，另一个是水平的白线），并将他们应用到两张图形中,使用 TensorFlow 的conv2d()函数构建的卷积图层（零填充，步幅为 2）。
import numpy as np
import tensorflow as tf
# Load sample images
from sklearn.datasets import load_sample_image
china=load_sample_image("china.jpg")
flower=load_sample_image("flower.jpg")
image = china[150:220, 130:250]
height, width, channels = image.shape #70*120*3
image_grayscale = image.mean(axis=2).astype(np.float32) #在深度维度（通道）上求平均,得 70*120
images = image_grayscale.reshape(1, height, width, 1)#是一个4维的数组，用于输入到tensorflow中的con2d函数
# Create 2 filters
fmap = np.zeros(shape=(7, 7, 1, 2), dtype=np.float32)#7行7列的卷积核，通道为1，batchsize=2
fmap[:, 3, 0, 0] = 1
fmap[3, :, 0, 1] = 1
# Create a graph with input X plus a convolutional layer applying the 2 filters
reset_graph()
X=tf.placeholder(tf.float32,shape=(None,height,width,1))
feature_map=tf.constant(fmap)
convolution=tf.nn.conv2d(X,feature_map,strides=[1,2,2,1],padding="SAME")
with tf.Session() as sess:
output=sess.run(convolution,feed_dict={X:images})
函数conv2d()参数说明：
X是输入小批次（4D 张量，如前所述）- 卷积核filters是应用的一组卷积核（也是一个 4D 张量，如前所述）。
- 步幅strides是一个四元素的一维数组，其中两个中间的值是垂直和水平的步幅（
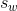
padding必须是"VALID"或"SAME"：
- 如果设置为
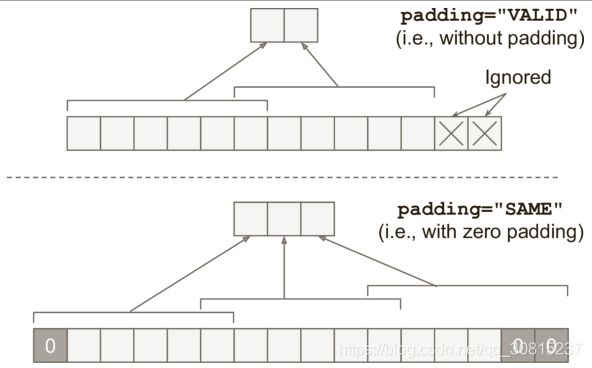
"VALID"，卷积层不使用零填充，并且可能会忽略输入图像底部和右侧的某些行和列，具体取决于步幅 - 如果设置为
"SAME"，则卷积层在必要时使用零填充。 在这种情况下，输出神经元的数量等于输入神经元的数量除以该步幅，向上舍入（在这个例子中，ceil(13/5)= 3）。 然后在输入周围尽可能均匀地添加零。
卷积图层有很多超参数：你必须选择卷积核的数量，高度和宽度，步幅和填充类型。 可以使用交叉验证来查找正确的超参数值，但这非常耗时。
一个完整实例：
import numpy as np
from sklearn.datasets import load_sample_images
# Load sample images
china = load_sample_image("china.jpg")
flower = load_sample_image("flower.jpg")
dataset = np.array([china, flower], dtype=np.float32)
batch_size, height, width, channels = dataset.shape #(2, 427, 640, 3)
# Create 2 filters
filters = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1 # vertical line
filters[3, :, :, 1] = 1 # horizontal line
# Create a graph with input X plus a convolutional layer applying the 2 filters
reset_graph()
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
convolution = tf.nn.conv2d(X, filters, strides=[1,2,2,1], padding="SAME")
with tf.Session() as sess:
output = sess.run(convolution, feed_dict={X: dataset}) #(2, 214, 320, 2)
plt.imshow(output[0, :, :, 1], cmap="gray") # plot 1st image's 2nd feature map
plt.show() 使用 tf.layers.conv2d()函数：
#tf.layers.conv2d与tf.nn.conv2d
reset_graph()
X = tf.placeholder(shape=(None, height, width, channels), dtype=tf.float32)
conv = tf.layers.conv2d(X, filters=2, kernel_size=7, strides=[2,2],
padding="SAME")
init = tf.global_variables_initializer()
with tf.Session() as sess:
init.run()
output = sess.run(conv, feed_dict={X: dataset})
plt.imshow(output[0, :, :, 1], cmap="gray") # plot 1st image's 2nd feature map
plt.show()tf.layers.conv2d和tf.nn.conv2d使用区别:
tf.layers.conv2d(inputs, filters, kernel_size, strides=(1,1),
padding='valid', data_format='channels_last',
dilation_rate=(1,1), activation=None,
use_bias=True, kernel_initializer=None,
bias_initializer=init_ops.zeros_initializer(),
kernel_regularizer=None,
bias_regularizer=None,
activity_regularizer=None, trainable=True,
name=None, reuse=None) 作用:2D卷积层的函数接口 这个层创建了一个卷积核，将输入进行卷积来输出一个 tensor。如果 use_bias 是 True（且提供了 bias_initializer），则一个偏差向量会被加到输出中。最后，如果 activation 不是 None，激活函数也会被应用到输出中。
参数说明：
inputs：Tensor 输入，4D张量filters：整数，表示输出空间的维数（即卷积核的数量）kernel_size：一个整数，或者包含了两个整数的元组/队列，表示卷积窗的高和宽。如果是一个整数，则宽高相等。strides：一个整数，或者包含了两个整数的元组/队列，表示卷积的纵向和横向的步长。如果是一个整数，则横纵步长相等。另外，strides不等于1 和dilation_rate不等于1 这两种情况不能同时存在。padding："valid"或者"same"（不区分大小写）。"valid"表示不够卷积核大小的块就丢弃，"same"表示不够卷积核大小的块就补0。
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)对于卷积来说，作用是一样的。一个参数要注意一下：
filter:是一个４维张量，其type必须和输入一样，[filter_height, filter_width, in_channels, out_channels(卷积核个数)]
filters:一个整数，输出空间的维度，也就是卷积核的数量。
from:https://blog.csdn.net/Touch_Dream/article/details/78446850
内存需求
CNN 的另一个问题是卷积层需要大量的 RAM，特别是在训练期间，因为反向传播需要在正向传递期间计算的所有中间值。例如，具有5×5卷积核的卷积层，输出 200 个150×100的特征图（即应用了200组不同卷积核，每组卷积核又包括RGB3个不同卷积核），步长为 1，使用SAME填充。 如果输入150×100RGB 图像 （三个通道），则参数的数量是(5×5×3 + 1)×200 = 15,200（+1对应于偏置项），这跟全连接层比较是相当小的。（具有150×100神经元的全连接层，每个连接到所有150×100×3输入，将具有150 ^ 2×100 ^ 2×3 = 675,000,000个参数！）然而，200 个特征图的尺寸150×100个像素神经元，这些神经元中的每一个都需要计算其5×5×3 = 75个输入的权重和：总共 2.25 亿次浮点乘法。不像全连接层那么糟糕，但仍然是计算密集型的。 而且，如果使用 32 位浮点数来表示特征映射，则卷积层的输出将占用 RAM 的200×150×100×32 = 9600万位（大约 11.4MB）。 这只是一个例子！ 如果训练批次包含 100 个实例，则该层将占用超过 1 GB 的 RAM！
在对新实例进行预测时，一旦下一层计算完毕，一层所占用的 RAM 就可以被释放，因此只需要两个连续层所需的 RAM 数量。 但是在训练期间，在正向传递期间计算的所有内容都需要被保留用于反向传递，所以所需的 RAM 量（至少）是所有层所需的 RAM 总量。如果由于内存不足错误导致训练崩溃，则可以尝试减少小批量大小。 或者，可以尝试使用步幅降低维度，或者删除几个图层。 或者使用 16 位浮点数而不是 32 位浮点数。 或者在多个设备上分发 CNN。
池化层
池化层的目标是对输入图像进行二次抽样（即收缩）以减少计算负担，内存使用量和参数数量（从而限制过度拟合的风险）。 减少输入图像的大小也使得神经网络容忍一点点的图像变换（位置不变）。
就像在卷积图层中一样，池化层中的每个神经元都连接到前一层中有限数量的神经元的输出，位于一个小的矩形感受野内。 您必须像以前一样定义其大小，跨度和填充类型。 但是，汇集的神经元没有权重; 它所做的只是使用聚合函数（如最大值或平均值）来聚合输入。下图显示最大池化，这是最常见的池化类型。 在这个例子中，我们使用一个2×2的核，步幅为 2，没有填充。 请注意，只有每个核中的最大输入值才会进入下一层。 其他输入被丢弃。
这显然是一个非常具有破坏性的层：即使只有一个2×2的核和 2 的步幅，输出在两个方向上都会减小两倍（所以它的面积将减少四倍），一下减少了 75% 的输入值。池化层通常独立于每个输入通道工作，因此输出深度与输入深度相同。但也可以选择在深度维度上进行叠加，在这种情况下，图像的空间维度（高度和宽度）保持不变，但是通道数目减少。
在 TensorFlow 中实现一个最大池层是非常容易的。 以下代码使用2×2核创建最大池化层，步幅为2，没有填充，然后将其应用于数据集中的所有图像：
import numpy as np
from sklearn.datasets import load_sample_image
import tensorflow as tf
import matplotlib.pyplot as plt
china = load_sample_image("china.jpg")
flower = load_sample_image("flower.jpg")
dataset = np.array([china, flower], dtype=np.float32)
batch_size, height, width, channels = dataset.shape
# Create 2 filters
filters = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters[:, 3, :, 0] = 1 # vertical line
filters[3, :, :, 1] = 1 # horizontal line
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
max_pool = tf.nn.max_pool(X, ksize=[1,2,2,1], strides=[1,2,2,1],padding="VALID")
with tf.Session() as sess:
output = sess.run(max_pool, feed_dict={X: dataset})
plt.imshow(output[0].astype(np.uint8)) # plot the output for the 1st image
plt.show()max_pool函数参数说明：
X是输入小批次（4D 张量，[mini-batch,size,height,width,channels]）-
ksize参数包含沿输入张量的所有四维的核形状：[min-batch, height, width, channels]。 TensorFlow 目前不支持在多个实例上合并，因此ksize的第一个元素必须等于 1。此外，它不支持在空间维度（高度和宽度）和深度维度上合并，因此ksize[1]和ksize[2]都必须等于 1，否则ksize[3]必须等于 1。 - 步幅strides是一个四元素的一维数组，其中两个中间的值是垂直和水平的步幅（
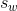
- padding:填充方式，同上所述
要创建一个平均池化层，只需使用avg_pool()函数而不是max_pool()。
CNN 架构
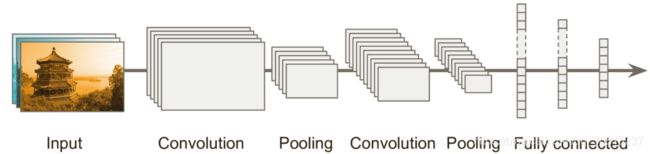
典型的 CNN 体系结构有一些卷积层（每一个通常跟着一个 ReLU 层），然后是一个池化层，然后是几个卷积层(+ReLU)，然后是另一个池化层。 随着网络的进展，图像变得越来越小，但是由于卷积层的缘故，图像通常也会越来越深（即更多的特征映射）。 在堆栈的顶部，添加由几个全连接层（+ ReLU）组成的常规前馈神经网络，并且最终层输出预测（例如，输出估计类别概率的 softmax 层）。
一个常见的错误是使用太大的卷积核。 通常可以通过将两个3×3内核堆叠在一起来获得与9×9内核相同的效果，计算量更少。
多年来，这种基础架构的变体已经被开发出来，导致了该领域的惊人进步。 这种进步的一个很好的衡量标准是比赛中的错误率，比如 ILSVRC ImageNet 的挑战。 在这个比赛中，图像分类的top-5误差率在五年内从 26% 下降到仅仅 3% 左右。 前五位错误率是系统前5位预测未包含正确答案的测试图像的数量。 图像很大（256 像素），有 1000 个类，其中一些非常微妙（尝试区分 120 个狗的品种）。 查看获奖作品的演变是了解 CNN 如何工作的好方法。
经典的 LeNet-5 架构（1998 年），然后是 ILSVRC 挑战赛的三名获胜者 AlexNet（2012），GoogLeNet（2014）和 ResNet（2015）。还有其他一些架构，特别是 VGGNet（2014 年 ILSVRC 挑战赛的亚军）和 Inception-v4（将 GooLeNet 和 ResNet 的思想融合在一起，实现了接近 3% 的 top-5 误差 ImageNet 分类率）。
卷积架构可参见：从LeNet到AlexNet
用CNN进行MNIST数字识别实例：
import tensorflow as tf
import numpy as np
height=28
width=28
channels = 1
n_inputs = height * width
conv1_fmaps = 32 #卷积核个数
conv1_ksize = 3 #卷积核宽高
conv1_stride = 1 #步幅
conv1_pad = "SAME"
conv2_fmaps = 64
conv2_ksize = 3
conv2_stride = 2
conv2_pad = "SAME"
pool3_fmaps = 64
n_fc1 = 64
n_outputs = 10
reset_graph()
with tf.name_scope("inputs"):
X=tf.placeholder(tf.float32,shape=[None,n_inputs],name="X")
X_reshaped=tf.reshape(X,shape=[-1,height,width,channels])
y=tf.placeholder(tf.int32,shape=[None],name="y")
conv1 = tf.layers.conv2d(X_reshaped, filters=conv1_fmaps, kernel_size=conv1_ksize,
strides=conv1_stride, padding=conv1_pad,
activation=tf.nn.relu, name="conv1")
conv2 = tf.layers.conv2d(conv1, filters=conv2_fmaps, kernel_size=conv2_ksize,
strides=conv2_stride, padding=conv2_pad,
activation=tf.nn.relu, name="conv2")
with tf.name_scope("pool3"):
pool3=tf.nn.max_pool(conv2,ksize=[1,2,2,1],strides=[1,2,2,1],padding="VALID")
pool3_flat=tf.reshape(pool3,shape=[-1,pool3_fmaps*7*7]) #卷积核个数*7*7，池化之后要把二维图像转化为一维列向量
with tf.name_scope("fc1"):
fc1=tf.layers.dense(pool3_flat,n_fc1,activation=tf.nn.relu,name="fc1")#全链接，每个特征图的一维列向量均与64个神经元相连
with tf.name_scope("output"):
logits=tf.layers.dense(fc1,n_outputs,name="output")
Y_proba=tf.nn.softmax(logits,name="Y_proba")
with tf.name_scope("train"):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=y)# 损失函数：计算交叉熵
loss = tf.reduce_mean(xentropy) #平均交叉熵
optimizer = tf.train.AdamOptimizer()
training_op = optimizer.minimize(loss)
with tf.name_scope("eval"):
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
with tf.name_scope("init_and_save"):
init = tf.global_variables_initializer()
saver = tf.train.Saver()
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.astype(np.float32).reshape(-1, 28*28) / 255.0
X_test = X_test.astype(np.float32).reshape(-1, 28*28) / 255.0
y_train = y_train.astype(np.int32)
y_test = y_test.astype(np.int32)
X_valid, X_train = X_train[:5000], X_train[5000:]
y_valid, y_train = y_train[:5000], y_train[5000:]
n_epochs = 10
batch_size = 100
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for X_batch, y_batch in shuffle_batch(X_train, y_train, batch_size):
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_batch = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Last batch accuracy:", acc_batch, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_mnist_model")运行不了，报错：Process finished with exit code -1073741819 (0xC0000005)
未能解决。。。。。。难受！
换了个电脑，又好使了。。。。
讲讲这个函数：
def shuffle_batch(X, y, batch_size):
rnd_idx = np.random.permutation(len(X))
n_batches = len(X) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
X_batch, y_batch = X[batch_idx], y[batch_idx]
yield X_batch, y_batch1、permutation(5);输出>>array([1, 2, 3, 0, 4])，//当x是整数，即打乱arange(x)
2、array_split(rnd_idx, n_batches)：对于长度为l 的数组，应该分成n个部分，它返回 l％n（取余数）个 大小为l // n + 1（取整）的子数组和其余大小为l // n的子数组。For an array of length l that should be split into n sections, it returns l % n sub-arrays of size l//n + 1and the rest of size l//n！？？？？
Examples：
>>> x = np.arange(8.0)
>>> np.array_split(x, 3) #n=3，8//(3+1)=2,所以有2个是长度为指定为3长度，剩下的为一个长度
[array([ 0., 1., 2.]), array([ 3., 4., 5.]), array([ 6., 7.])]
>>> x = np.arange(7.0)
>>> np.array_split(x, 3) #n=3, 7//(3+1)=1,所以有一个是长度为指定3的长度，剩下的为平均长度
[array([ 0., 1., 2.]), array([ 3., 4.]), array([ 5., 6.])]
原文：https://blog.csdn.net/hqhc9747/article/details/80294807
3、yield 的作用就是把一个函数变成一个 generator，带有 yield 的函数不再是一个普通函数，Python 解释器会将其视为一个 generator，调用 shuffle_batch(X_train, y_train, batch_size)不会执行 shuffle_batch函数，而是返回一个 iterable 对象！
在 for 循环执行时，每次循环都会执行shuffle_batch 函数内部的代码，执行到 yield X_batch, y_batch 时，shuffle_batch 函数就返回一个迭代值，下次迭代时，代码从 yield X_batch, y_batch 的下一条语句继续执行，而函数的本地变量看起来和上次中断执行前是完全一样的，于是函数继续执行，直到再次遇到 yield。
from：http://www.runoob.com/w3cnote/python-yield-used-analysis.html
tf.unstack()是一个拆分矩阵的函数，将秩为 R 的张量的给定维度出栈为秩为 (R-1) 的张量。
unstack(
value,
num=None,
axis=0,
name='unstack' )value：代表需要分解的矩阵变量（其实就是一个多维数组，一般为二维）；
axis：指明对矩阵的哪个维度进行分解。
通过沿 axis 维度将 num 张量从 value 中分离出来。如果没有指定 num（默认值），则从 value 的形状推断。
此外，tf.stack函数刚好是与tf.unstack函数相反，前者是对矩阵进行拼接，后者则对矩阵进行分解。
例如，给定一个具有形状 (A, B, C, D) 的张量。
- 如果 axis == 0，那么 output 中的第 i 个张量就是切片 value[i, :, :, :]，并且 output 中的每个张量都具有形状 (B, C, D)。
- 如果 axis == 1，那么 output 中的第 i 个张量就是切片 value[:, i, :, :]，并且 output 中的每个张量都具有形状 (A, C, D)。
tf.transpose()函数
tf.transpose(input, perm=[dimension_1, dimenaion_2,..,dimension_n]):
这个函数主要适用于交换输入张量的不同维度用的，如果输入张量是二维，就相当是转置。perm:控制转置的操作, dimension_n是整数，如果张量是三维，就是用0,1,2来表示。这个列表里的每个数对应相应的维度。以perm = [0,1,2] 3个维度的数组为例, 0--代表的是最外层的一维, 1--代表外向内数第二维, 2--代表最内层的一维,这种perm是默认的值.如果是[2,1,0]，就把输入张量的第三维度和第一维度交换。假设input是一个 2x3x4的一个tensor, 假设perm = [1,0,2], 就是将最外2层转置,得到tensor应该是 3x2x4的tensor。
from：https://blog.csdn.net/banana1006034246/article/details/75126815