如何脱离数学推导理解欧拉角与万向节死锁

如何脱离数学推导理解欧拉角与万向节死锁

先来总结【看完全篇再来看下这几行】：
1、只有基于模型的旋转才会导致死锁。
2、基于欧拉角的每一种旋转顺序只会出现一种死锁情况（即中间旋转90度）。
3、死锁的表现为，依照顺序1的旋转面进行旋转后，顺序2的旋转导致顺序3将要旋转的旋转面与顺序1的旋转面重合，因此，顺序3的旋转与顺序1的旋转在模型的表现上变为一致，脱离了人类规定的运动规则。
4、死锁这俩字的本质为自由度的丢失。
5、更本质一点，死锁的出现是因为一个旋转被分成了三个基于独立轴的旋转，所以只要你是用基于3个轴的旋转相乘来表示一个旋转，那就会死锁。
6、欧拉角无法直接作用于向量，可以直接作用于向量的只有四元数与矩阵，只有将欧拉角转换为三个矩阵才会导致死锁，转换为四元数不会导致死锁（但某些顺序是无法转四元数的）。

0、需要提前掌握的知识

欧拉角是用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角φ组成，为欧拉首先提出而得名。（百度百科）

其实就是把空间中的一个旋转，用三个绕三根轴的旋转角度来表示，的这样一种方法，欧拉角由三个角组成。

别的应该没有了，想到再加。

1、死锁的本质-旋转面重合的成因

首先要明确，旋转分两种，1，基于模型旋转，2，基于世界旋转。

基于模型旋转的时候，会出现万向节死锁现象。

这里要明确第二件事，所谓的基于模型旋转，并不是一般想象中基于三根永远互相垂直的轴（或者说永远互相垂直的旋转面），就像世界坐标轴那样。而是基于下图这样的三个可以自由旋转的轴（注：该图中是用旋转面来体现的，轴为垂直于旋转面），因此，它们存在两个旋转面重合的情况。

（gif截自https://v.youku.com/v_show/id_XNjk1MTkzMTM2.html#paction，这个比b站的机翻版好很多，建议看一下，加深对万向节原理的理解）

这种重合仅出现在中间那次旋转为90度时，这是因为，旋转顺序具有层级，子层级无法带动父层级运动（可以看视频来加深对这句话的理解）。以y（绿，偏航），x（红，俯仰），z（蓝，桶滚）的顺序来举例，层级为y最高，x中间，z其次，在运动的初始，转动绿轴（绕y轴），会使箭头做偏航的运动，且作为最高层级，它会带动另外两个轴，因此，顺序1的运动无法导致两个旋转面重合。

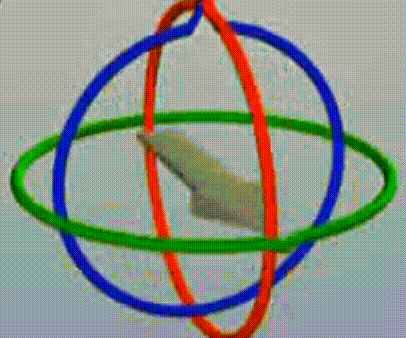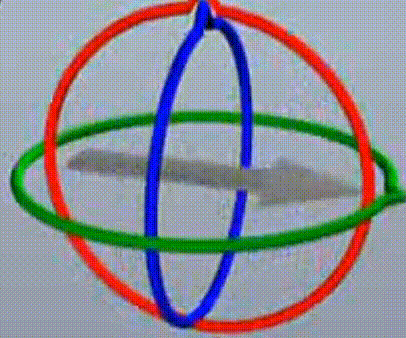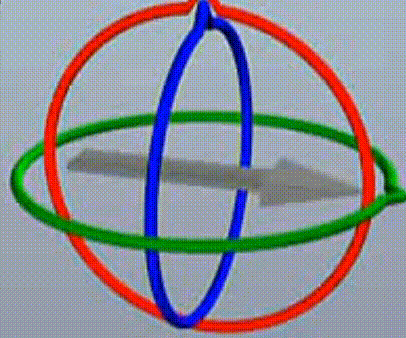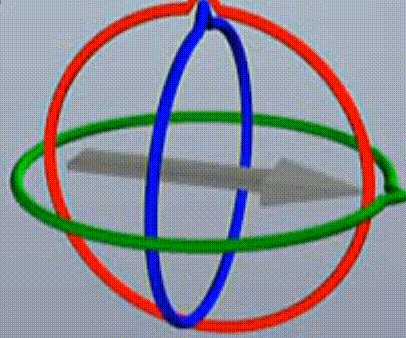
顺序2为绕x轴运动，可以看到，转动红色的圈（这里再次强调下，我这里表述不严谨，转动红圈其实是绕着红轴旋转，这里红圈是旋转面，红轴即x轴是垂直于这个红色的圆圈的），转动红圈，可以看到箭头做俯仰运动，以及它无法带动绿色的父级一起旋转，这就导致了，一组旋转顺序中，顺序2的旋转有可能导致另外两个旋转面重合，并且，显然是旋转直角的度数（不一定是90，90+360也行呀，270也行呀）。

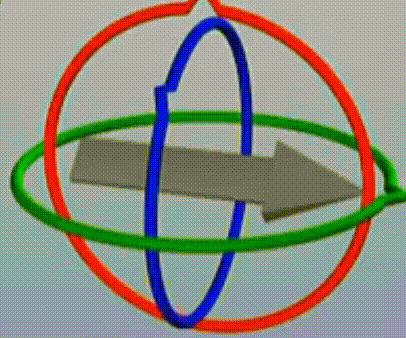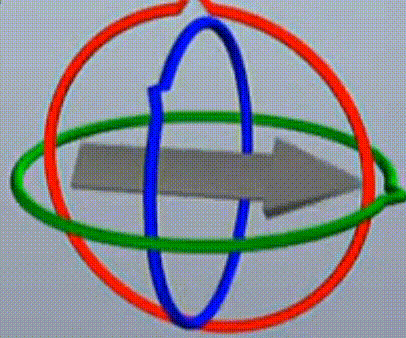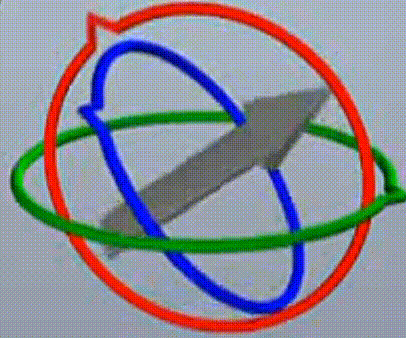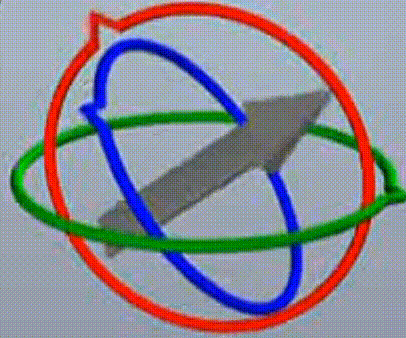
如下图，两个旋转面重合。旋转面重合是死锁的本质成因，后面会进行更深入的分析，到这里，需要理解的是两个旋转面重合的成因。

总结一下，三个旋转中，只有第二次旋转有可能导致两个旋转面重合，因为第一次旋转是最高层级，它会带动另外俩轴一起运动，让三个旋转面始终保持垂直。第二次旋转是次高层级，它无法带动第一次旋转的面，而可以带动再次一层的面，因此它可能导致两个面重合。第三次旋转是最底层的，它谁也带不动，只能在它自己的平面上旋转，所以单独旋转最次一层的圈，也不会导致两个面重合。

观察一下重合后的状态，接下来按照计划，顺序3为转动蓝轴（绕z轴）运动，这会让箭头做滚桶运动。

2、死锁出现将导致什么？-失控

总结一下，在这三次运动中，我们分别进行了偏航，俯仰，桶滚运动，看似很ok？何来丢失自由度一说？明明三种运动都照顾到了呀。这里应当这样理解，想在顺序1中完成俯仰，一定有一根确定的轴可以使用（即只需要围绕某一根轴调整角度，即可完成俯仰），这是因为每一次基于三个欧拉角的旋转，都是由垂直的三个旋转面开始的。因此，顺序1中，可任意通过一根确定的轴来完成三个运动中的任一个（俯仰，桶滚，偏航），因此，顺序1存在三个可自由调整的自由度。

接下来，在顺序2中，也可以通过一根确定的轴来指定任意一种运动，因为，在顺序1的旋转结束后，三个旋转面依旧是互相垂直的，只不过在顺序1的带动下，与初始坐标轴的角度有所区别，但依旧是互相垂直的（因为顺序1会带动另外两个轴一起动）。

因此，如顺序1一样，在三个旋转面互相垂直的情况下，顺序2也有三个自由度可挑选，你依然可以基于一根确定的轴来进行任一类型的运动，因此，顺序2也存在三个可自由调整的自由度。

（补充：基于哪根轴做哪种运动，通常是人工定义的，这里不必拘泥，理解即可，但是要统一！不能一会儿x偏航一会儿x滚动这样，对一个模型来讲运动是要统一的，这样才能用欧拉角来指挥模型做某种确定的运动）

综上，在前两次动作中，你可以俯仰，俯仰，或者俯仰桶滚，俯仰偏航，这都是可以用一根确定的轴来完成的。例如30,30,的围绕X，X的旋转，意为俯仰30度，再俯仰30度，30,30,基于X，Y是俯仰30后偏航30，或者基于Y，Z是偏航后桶滚，基于X，Z，怎样组合都行，都可以正确表达运动类型。

但是，如果顺序2的运动导致了两个旋转面重合，那么，在下一次运动时，则无法通过选择绕某个轴，来正确表达某种确定的运动，也即绕某个轴与某种运动种类，无法严格一一对应了。

如本文中的例子，按90度转动红轴后（不厌其烦的再次提醒下，转动红轴意为绕x轴旋转，只是说转动红轴比较形象，x轴垂直于红圈，红圈是绕x轴旋转的旋转面），蓝旋转面（绕z轴）与绿旋转面（绕y轴）重合了。

此时，顺序3的操作，就无法由一个确定的轴来直接决定了。

例如，30,90,60，基于X，Y，Z的旋转，按照这个设计理论，我们是希望模型先俯仰（绕x），再偏航（绕y），最后桶滚（绕z），这是本文中的例子，通过上面婆婆妈妈的分析，你会发现，对呀！确实是俯仰，偏航，桶滚呀？没有死锁（失控/运动与绕确定轴无法一一对应，总之随便你怎么讲）呀？

那如果是30,90，60基于X，Y，X呢？设计理论应该是，俯仰（绕x），偏航（绕y），再俯仰（绕x），但实际上呢？

实际上，前两个运动确实如我们所愿，是俯仰30度，偏航90度，但是！由于此时桶滚面与俯仰面重合了，（蓝面绿面重合），因此，再转动绿轴（绕x运动），无法俯仰了！变成桶滚了！

如下图所示，在这种情况下，顺序3将无法通过一个确定的轴做俯仰运动，在这个情况下，原本绕蓝（z）轴应该是桶滚，这是ok的，绕y（绿）轴应该是偏航，但如图所示，此时还是滚动，绕x轴（红）应该是俯仰，但如图，现在变成偏航了！

上面婆妈了一句还不够，再强调下，对于一个模型，或者一个物理体系下，绕某个轴旋转==做某种运动，这个必须是严格一一对应的，这样才能使欧拉角有控制运动的效果。

倒不是说全世界都必须用同一种设定，只是说对于一个可旋转的局部区域、物体等来讲，这个对应必须是严格唯一的，不能一会儿x轴代表俯仰，一会儿x轴代表滚桶，如果这个对应不是唯一的，那你写代码的时候，或者控制飞机飞行的时候，该怎么控制？

拿着飞机遥控器，难道还要实时判断一下，此时按哪个键才是俯仰吗？

综上所述，在两个旋转面重合时，顺序3的运动，将无法使用如同顺序1与顺序2的运动设定了，顺序3的运动，失控了。

这就叫万向节死锁，这个名怪好听的，但其实如果你真的理解了我上面的分析，读到这里，应该知道万向节死锁这个名字蛮难理解的，倒不如说基于欧拉角来控制物体运动，有可能导致失控（即想俯仰，结果偏航了之类的）比较好理解些。

3、旋转面逐渐慢慢走向重合，这个过程是怎样的？

如果空间几何思维够好的话，可以想象一下，如果离重合只差一咪咪呢？如下图。再贴一下本文中一一对应的设定：y（绿，偏航），x（红，俯仰），z（蓝，滚桶）。

顺序2未导致蓝绿面重合，虽然只差一咪咪，但顺序3中，转动绿圈依然可以让箭头在一个很小的范围内做偏航。

发挥你聪明的大脑想一下，不行就掏一根笔出来，这支笔平放在桌面上，围绕垂直桌面的轴运动，可以看到笔在做“偏航”运动，逐渐把这只笔提起来，让笔尖向上，但并不垂直，此时还是围绕垂直桌面的轴旋转，笔尖的运动状态是在空气中画了一个小圆圈，也就是依然是可以做“偏航”运动的，但当笔尖垂直于桌面呢，此时围绕垂直桌面的轴，就只能做桶滚运动了！

为了避免萌新混乱，这里讲下为什么在笔尖向上提的过程中，偏航轴永远垂直于桌面，因为在本例中，顺序3是最底层的运动了，它无法带动前面顺序1与顺序2的圈的运动，而笔尖提起（俯仰，x，红）是顺序2，也无法带动顺序1的绿圈，因此笔尖提起（俯仰）然后在空中画圈（偏航）这个过程，绿圈永远不动，绿轴（y，偏航）永远垂直于桌面。

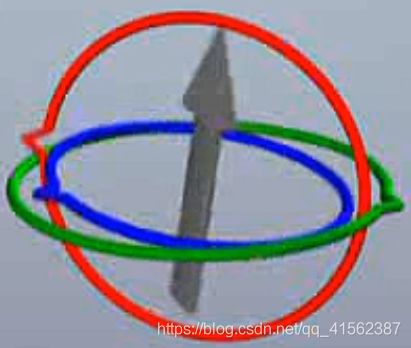
总结一下，万向节死锁只由顺序2的运动造成，而本质是两个旋转面的重合，以及失控只发生在顺序3的运动，即在顺序3中，无法用一组严格一一对应的轴==运动来控制模型进行某种指定的运动（桶滚，俯仰，偏航）。

在顺序3中，它还是在运动的，但已经脱离人类那套规则的掌控了！这就是万向节死锁造成的严重问题。

4、补充知识

4.1 欧拉角，旋转矩阵，四元数，以及它们的数学意义

https://www.bilibili.com/video/BV1oa4y1v7TY?p=1 这个视频站在矩阵运算的角度详细介绍了欧拉角，旋转矩阵，四元数，以及它们之间的相互转换，还有基于世界运动与基于模型运动分别是怎样给点乘以怎样的旋转矩阵，以及还给出了一个有价值的定理：顺序的基于模型的运动，==逆序的基于世界的运动，这些不一定有助于你更进一步理解万向节，但有助于加深对旋转的理解，以及，也许有助于你去书写自己的旋转函数，强烈建议有空看下。

4.2 死锁可以通过四元数来完全避免吗

欧拉角是无法直接用于旋转计算的，本质需要转换成旋转矩阵或者四元数才能作用于向量，其中，转换为四元数是不会引起万向节死锁的，因为万向节死锁本身只会出现在将一个旋转拆分为三次旋转的情况下，而四元数是基于一个轴的旋转，不会引起万向节死锁。

而转换为三个旋转矩阵，再将其按照一定的顺序作用于向量，是会导致万向节死锁的。

又或者是，只有转换为三个旋转矩阵再作用于向量，才会导致死锁，这是导致死锁的唯一原因。

此外，其余不会触发万向节死锁的旋转方法有：轴角，基于一个3x3矩阵，或基于一个表示旋转的4x4矩阵。

补充：将欧拉角的三个旋转矩阵乘完变成一个3x3或4x4矩阵也还是会导致死锁的，并不是乘完变成一个矩阵就没有这个现象了。

综上，既然欧拉角转四元数即可避免死锁，那么这是可以完全避免的吗？并不是，因为并不是每一种欧拉角的旋转顺序都可以计算出四元数，这里看一下欧拉角转四元数中，判断旋转顺序的源码，可以发现，可转四元数的顺序不包括重复的，也就是类似XYX这样的顺序，因此如果要实现诸如XYX,ZYZ这样的运动，首先这玩意不能转四元数，因此只能用三个旋转矩阵来计算，而这种情况下，还是要面临万向节死锁！

因此，实际上万向节死锁是无法完全消灭的，总要去面对它。

switch (order) {
     
				case 'XYZ':
					this._x = s1 * c2 * c3 + c1 * s2 * s3;
					this._y = c1 * s2 * c3 - s1 * c2 * s3;
					this._z = c1 * c2 * s3 + s1 * s2 * c3;
					this._w = c1 * c2 * c3 - s1 * s2 * s3;
					break;
				case 'YXZ':
					this._x = s1 * c2 * c3 + c1 * s2 * s3;
					this._y = c1 * s2 * c3 - s1 * c2 * s3;
					this._z = c1 * c2 * s3 - s1 * s2 * c3;
					this._w = c1 * c2 * c3 + s1 * s2 * s3;
					break:
				case 'ZXY':
					this._x = s1 * c2 * c3 - c1 * s2 * s3;
					this._y = c1 * s2 * c3 + s1 * c2 * s3;
					this._z = c1 * c2 * s3 + s1 * s2 * c3;
					this._w = c1 * c2 * c3 - s1 * s2 * s3;
					break;
				case 'ZYX':
					this._x = s1 * c2 * c3 - c1 * s2 * s3;
					this._y = c1 * s2 * c3 + s1 * c2 * s3;
					this._z = c1 * c2 * s3 - s1 * s2 * c3;
					this._w = c1 * c2 * c3 + s1 * s2 * s3;
					break;
				case 'YZX':
					this._x = s1 * c2 * c3 + c1 * s2 * s3;
					this._y = c1 * s2 * c3 + s1 * c2 * s3;
					this._z = c1 * c2 * s3 - s1 * s2 * c3;
					this._w = c1 * c2 * c3 - s1 * s2 * s3;
					break;
				case 'XZY':
					this._x = s1 * c2 * c3 - c1 * s2 * s3;
					this._y = c1 * s2 * c3 - s1 * c2 * s3;
					this._z = c1 * c2 * s3 + s1 * s2 * c3;
					this._w = c1 * c2 * c3 + s1 * s2 * s3;
					break;
				default:
					console.warn('THREE.Quaternion: .setFromEuler() encountered an unknown order: ' + order);
			}

4.3 欧拉角适合决定姿态，但不一定适合计算插值

我们并不一定用一点点修改欧拉角来做动画的，因为这让人难以掌控，比如，用欧拉角表示的姿态1，与用欧拉角表示的姿态2，中间用怎样的方式计算插值呢？显然无法用欧拉角的简单连续变化来完成。

只修改一个角度的话，用基于欧拉角的旋转来转动到下一个姿态还是可以的，但两个以上的欧拉角就不是那么个回事儿了，你可以尝试一下能不能脑补出来俩欧拉角甚至仨欧拉角都在变化时，怎么计算欧拉角的插值。

基于上述原因，各大引擎中给了我们基于四元数的插值计算方法，一个叫slerp，一个叫lerp，lerp是线性插值，也就是，把两个姿态，认定为两个点，然后把这俩点连线，在线上按照百分比返回下一个点，这是一种线性的过渡方法，叫线性插值。

slerp是球面插值，在这里，认为两个姿态是两个向量，然后按角度的百分比返回下一个点，就像这个点在球面上，按照一段弧线过渡到另一个点一样。

用threejs的话，也是有这两种插值计算法的，一个在V3点的类下，一个在四元数的类下，好好在文档里找下类里的方法即可。

但还是要注意一下，slerp是按照两点在球上的最短弧来计算插值（过渡）的，如果要绕个圈圈再到达最终姿态，则还是要通过欧拉角来计算插值，理解深入后，使用哪种方法，就看需求了。

5、写在最后

因为更多是将这些概念作为工具，去控制某种运动，因此，如果完全基于数学推导去理解所谓死锁，插值等等，可能会比较困难，无法形成概念。希望看完这篇文章的萌新可以有所体会，也希望大佬可以给点宝贵建议。