“吴恩达deeplearning.ai”学习笔记（p36-p44：第一课时第四章：深度神经网络）

目录

上接（第一课时第三章：实现一个神经网络）
下接 (第二课时第一章：超参数调试、正则化以及优化）
第四章：深度神经网络

• 4.1深层神经网络
• 4.2前向和反向传播
  • 4.2.1前向传播
  • 4.2.2反向传播
• 4.3深层网络中的前向传播
• 4.4核对矩阵的维数
• 4.5向量化实现的解释
• 4.6搭建深层神经网络块
• 4.7参数vs超参数
• 4.8深度学习和大脑的关系

---

补充一篇其他博主对于深度神经网络为什么能预测结果的理解：
link戳这里查看

第四章：深度神经网络

4.1深层神经网络

层数=隐藏层数+输出层
用来描述深度神经网络的符号约定：
①L——表示神经网络的层数
②n^[l]——表示节点的数量，或者l层上的单元数量
③a^[l]——表示l层中的激活函数（实例中我们往往会看到”a^[l]=g(z^[l]”)的写法），激活函数也会用层数l进行标注，其中a^[L]即为预测输出
④w^[l]——表示在a^[l]中计算z^[l]值的权重
⑤b^[l]——表示l层上的偏置向量

此例中：

L=4
n^[0]=3；n^[1]=5；n^[2]=5；n^[3]=3；n^[4]=n^[L]=1

---

4.2前向和反向传播

4.2.1前向传播

输入为：a^[l-1]
输出为：a^[l],z[l](同时缓存中可能会存下w^[l],b^[l]用于函数调用计算)
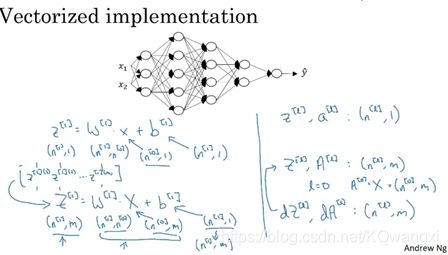
公式：

z[l]=w^[l]*a^[l-1]+b[l]
a[l]=g^[l](z^[l])

向量形式：

Z[l]=W^[l]*A^[l-1]+b[l]
A[l]=g^[l](Z^[l])

4.2.1反向传播

输入为："da^[l]"
输出为："da^[l-1]","dw[l]",db[l]
公式：

"dz[l]"="da[l]"*g[l]'(z[l])
"dw[l]"="dz[l]"*(a^[l-1])
db^[l]="dz^[l]"
"da[l-1]"=w^[l]T*"dz^[l]"
"dz[l]"= w^[l+1]T*"dz^[l+1]"*g[l]‘(z[l])

向量形式：

"dZ[l]"="dA[l]"*g[l]'(Z[l])
"dW[l]"=1/m*"dZ[l]"*(A^[l-1]T)
db^[l]=1/m*np.sum("dZ^[l]",axis=1,keepdims=True)
"dA[l-1]"=W^[l]T*"dZ^[l]"

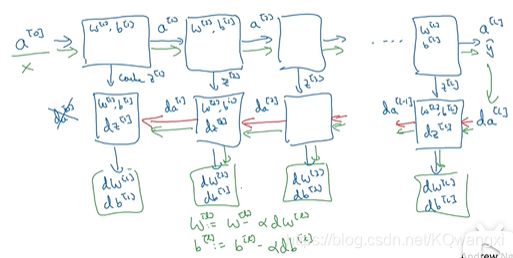
总结一下整个过程就是（以上图为例）：
（前向传播）用x作为输入，输入经过不同的隐藏层遇到不同的激活函数（有可能是ReLU、tanh、sigmoid这种啊等等）就可以得到预测输出a
再用a计算出损失，就可以进行反向迭代（也就是反向传播求导），用来求dw^[3]、db^[3]；dw^[2]、db^[2]；dw^[1]、db^[1]；此时cache会将z^[1]、z^[2]、z^[3]传递过来，再经过隐藏层的回溯逐步得到数据da^[2]、da^[1]。

---

4.3深层网络中的前向传播

以上图为例，认识深层网络，假设现有一个单独的训练样本x，
先计算第一层：
(在输入层，x可以看作x=a^[0])
x：z[1]=w^[1]*x+b[1] ，w^[1]与b[1]就是会影响在第一层的激活单元的参数；然后计算这一层的激活函数：a[1]=g^[1](z^[1])，激活函数g的指标l取决于所在的层数
再处理第二层：

z[2]=w^[2]*a^[1]+b[2]
a[2]=g^[2](z^[2])
……

后面的隐藏层以此类推
……
直到输出层：

z[4]=w^[4]*a^[3]+b[4]
a[4]=g^[4](z^[4])

a[4]即为想要估算的输出值

上述过程采用向量化的方法训练整个训练集表现为：

X=A^[0]
Z[l]=W^[l]*A^[l-1]+b[l]      
A[l]=g^[l](Z^[l])

---

4.4核对矩阵的维数

W^[l]的维度必须是(n^[l],n^[l-1])；b^[l]的维度一般是（n^[l],1）
“dw[l]”的维度与w^[l]保持一致,db与b的维度一致
Eg：
W^[2]的维度是（5，3），W^[2]应该是一个5*3的矩阵
而如果训练样本的数量变为m个，则相应的一些矩阵的维度会发生改变，比如：z^[l],a^[l]，如下图所示：

---

4.5向量化实现的解释

首先我们需要明白深层网络计算的是什么，
①以下图为例：（如果正在建一个人脸识别或者人脸检测系统）

1. 输入一张脸部的照片；
2. 深度神经网络的第一层作为一个特征探测器（或者边缘探测器）将图片进行划分，划分为同一层中的不同隐藏单元；
3. 隐藏单元会去寻找划分块照片中边缘的方向；
4. 然后将隐藏单元中的找到的照片边缘的像素组合，就汇聚为面部的不同部分（比如：有一个神经元会去寻找眼睛的部分，另一个神经元去找鼻子的部分）；
5. 再将这些部分放在一起，比如鼻子眼睛嘴巴下巴，就可以实现识别或是探测不同的人脸的功能。

②如果正在尝试搭建一个语音识别系统：

1. 输入一个音频片段；
2. 神经网络第一层开始试着探测一些比较低层次的音频波形的一些特征，比如分辨音调的高低，分辨白噪音等；
3. 选择上述找到的相对程度比较低的波形特征，并将其波形组合，就能去探测声音的基本单元（比如相较于单词cat而言，c/k/就是一个音位）；
4. 有了基本的声音单元，组合起来就能识别音频中的单词；
5. 单词的组合成为词组，进而组成句子。

---

4.6搭建深层神经网络块

---

4.7参数vs超参数的关系

已知神经网络的运算中重要的参数的为：w^[l]、b^[l]
而能够影响控制这些参数（w和b）的我们称之为超参数（即可以控制参数的参数），例如：
学习率α（出现在梯度下降法中）；梯度下降循环的次数；隐藏层数L；隐藏单元数n^[l]；隐藏层中的激活函数a
深度网络的实现更像是一个参数实验的过程：通过不断的设置参数值去找到最优的损失方案，而这个过程又常常会受到仪器配置和时间的影响。

---

4.8深度学习和大脑的关系

早期两者会被相提并论，但神经网络理论发展至今，二者已经不具有类比关系，因为大脑的学习过程与规模更加奇妙复杂。
实现一个神经网络时
我们所作的东西如下图所示（左基础公式，右向量表示）

脑袋中的生物神经元：
神经元会接受多个树突发来的信号，并将反应通过轴突传递给下一个神经元。

我们只能说生物神经元的确具有类似logistics回归函数的功能，但其功能绝不仅限于此，同时我们也无法从科学的角度分析出单个生物神经元完成了哪些功能

---