DGL-图属性

1. 图的创建

1.1 同质图

存储图的类：dgl.DGLGraph

1.1.1 直接创建：dgl.graph()

创建图的函数：dgl.graph()

首先创建边：0->1, 0->2, 0->3, 1->3

import torch
u, v = torch.tensor([0,0,0,1]), torch.tensor([1,2,3,3])

在dgl的图中，所有边都是有向的，如果要创建无向图，需要创建双向边

import torch
src, dst = torch.tensor([0,0,0,1]), torch.tensor([1,2,3,3])
u = torch.cat((src,dst))
v = torch.cat((dst,src))

创建图

import dgl
g = dgl.graph((u,v))

除了通过双向边外，还可通过dgl.to_bidirected直接由单向图创建双向图

bg = dgl.to_bidirected(g)

如果在图中有没有边链接的点，需要通过graph函数的num_nodes属性指定有多少单点

# 有4个edge，总共有8个点，则有4个单点
g = dgl.graph((u, v), num_nodes=8)

1.1.3 节点与边的特征

通过ndata与edata可以指定节点与边的特征

"建图"
g = dgl.graph(([0, 0, 1, 5], [1, 2, 2, 0])) # 6 nodes, 4 edges

"指定特征"
g.ndata['x']=torch.ones(g.num_nodes(), 3)
g.ndata['y']=torch.randn(g.num_nodes(),5) # 不同名字可以有不同的特征
g.edata['x']=torch.ones(g.num_edges(),dtype=torch.int32)

"查看特征"
print(g.ndata) # 输出dict  {'x':tensor, 'y':tensor}
print(g.edata) # {'x': tensor([1, 1, 1, 1], dtype=torch.int32)}

print(g.ndata['x'][1]) # tensor([1., 1., 1.])
print(g.edata['x'][torch.tensor([0, 3])])  # 查看第0和3号的特征
# tensor([1, 1], dtype=torch.int32)

注意事项：

• 只有数字类型可以做特征（e.g., float, double, and int），特征可以是标量，向量，矩阵或多维张量
• 点特征之间，边特征之间名字要不同，但点特征与边特征之间名字可以相同
• 无法给点/边的子集设置特征，特征tensor的最高维必须等于点/边数
• 特征张量是row-major的，即每一行是一个点/边的特征

对于有权图，可将权值作为图的边特征存储

# edges 0->1, 0->2, 0->3, 1->3
edges = th.tensor([0, 0, 0, 1]), th.tensor([1, 2, 3, 3])
weights = th.tensor([0.1, 0.6, 0.9, 0.7]) # weight of each edge
g = dgl.graph(edges)
g.edata['w'] = weights
print(g)
# Graph(num_nodes=4, num_edges=4,
#      ndata_schemes={}
#      edata_schemes={'w' : Scheme(shape=(,), dtype=torch.float32)})

1.2 异质图

1.2.1 异质图 Heterogeneous Graphs

指点/边有不同的类型，每种类型可以有独立的ID及特征，如下图所示，该图有两种类型的节点：User与Game，两种类型有各自的特征，且ID均从0开始

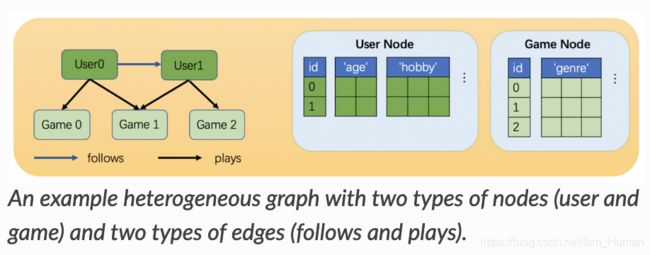
1.2.2 创建异质图-dgl.heterograph()

dgl中，每个关系指定一个图，异质图将由多个关系的图组成

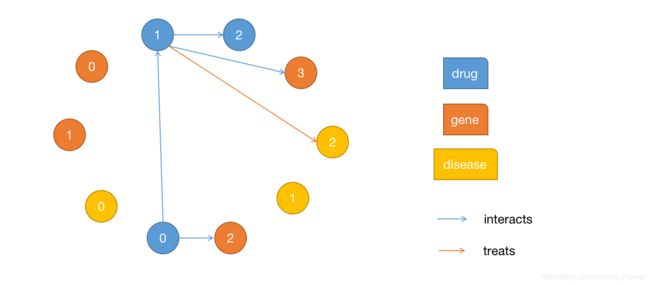
首先，每个关系写成一个三元组(原节点类型，关系类型，目标节点类型），如('drug', 'treats', 'disease')
该关系称为规范边类型（canonical edge types）

接着写出图数据，该数据中每个关系都对应一个图

{
     relation1 : (u, v),
 relation2 : (u, v),
 ...}

最后，使用dgl.heterograph()创建异质图

import torch as th
import dgl

# Create a heterograph with 3 node types and 3 edges types.
graph_data = {
     
   ('drug', 'interacts', 'drug'): (th.tensor([0, 1]), th.tensor([1, 2])),
   ('drug', 'interacts', 'gene'): (th.tensor([0, 1]), th.tensor([2, 3])),
   ('drug', 'treats', 'disease'): (th.tensor([1]), th.tensor([2]))
}
hg = dgl.heterograph(graph_data)
print(hg)
# Graph(num_nodes={'disease': 3, 'drug': 3, 'gene': 4},
#       num_edges={('drug', 'interacts', 'drug'): 2, ('drug', 'interacts', 'gene'): 2, ('drug', 'treats', 'disease'): 1},
#       metagraph=[('drug', 'drug', 'interacts'), ('drug', 'gene', 'interacts'), ('drug', 'disease', 'treats')])

1.3 Using DGLGraph on a GPU

方法1:构建GPU上的tensor，再传给DGLGraph

>>> u, v = u.to('cuda:0'), v.to('cuda:0')
>>> g = dgl.graph((u, v))
>>> g.device
device(type='cuda', index=0)

方法2:将DGLGraph传到GPU上

>>> u, v = th.tensor([0, 1, 2]), th.tensor([2, 3, 4])
>>> g = dgl.graph((u, v))
>>> g.ndata['x'] = th.randn(5, 3)  # original feature is on CPU
>>> g.device
device(type='cpu')
>>> cuda_g = g.to('cuda:0')  # accepts any device objects from backend framework
>>> cuda_g.device
device(type='cuda', index=0)
>>> cuda_g.ndata['x'].device       # feature data is copied to GPU too
device(type='cuda', index=0)

1.4 从外部资源创建

Scipy sparse matrix 作为图的邻接矩阵 转换成dgl的图 : g = dgl.from_scipy(sp.g)
Networkx graph : g = dgl.from_networkx(nx.g)

import dgl
import scipy.sparse as sp

sp_g = sp.rand(100, 100, density=0.5) # 5% nonzero entries
g = dgl.from_scipy(sp_g)
print(g)
# Graph(num_nodes=100, num_edges=5000,
#       ndata_schemes={}
#       edata_schemes={})

import networkx as nx
nxg = nx.path_graph(5) # a chain 0-1-2-3-4 
# nx.path_graph constructs an undirected NetworkX graph 
g = dgl.from_networkx(nxg)
print(g)
# Graph(num_nodes=5, num_edges=8,
#       ndata_schemes={}
#       edata_schemes={})

nxg = nx.DiGraph([(2, 1), (1, 2), (2, 3), (0, 0)])
# constructs an directed NetworkX graph 
g = dgl.from_networkx(nxg)
print(g)
# Graph(num_nodes=4, num_edges=4,
#      ndata_schemes={}
#      edata_schemes={})

从内存导入图
列举几种常见的存储格式：

• csv文件
  使用csv文件存储图：
  

从csv文件中加载图: ->pandas -> dgl

• JSON/GML 格式

->Networkx->dgl

• DGL Binary Format
  APIs : dgl.save_graphs() dgl.load_graphs()

2 图的属性

创建一个图

u, v = torch.tensor([0,0,0,1,2]), torch.tensor([1,2,3,3,1])
g = dgl.graph((u,v))
g.ndata['n_fe'] = torch.ones((g.num_nodes(), 3))
g.ndata['n_fe_matrix'] = torch.rand((g.num_nodes(), 3, 2))
g.edata['e_fe'] = torch.zeros(g.num_edges(), 5)

查看图信息

print(g)

"""
Graph(num_nodes=4, num_edges=5,
      ndata_schemes={'n_fe': Scheme(shape=(3,), dtype=torch.float32),
                     'n_fe_matrix': Scheme(shape=(3, 2), dtype=torch.float32)}
      edata_schemes={'e_fe': Scheme(shape=(5,), dtype=torch.float32)})
      """

2.1 关于图的节点与边的信息

同质图	异质图	功能	例
[’_N’]	hg.ntypes	节点类型	[‘disease’, ‘drug’, ‘gene’]
[’_E’]	hg.etypes	边的类型	[‘interacts’, ‘interacts’, ‘treats’]
–	hg.canonical_etypes	规范边类型(三元组)	[(‘drug’, ‘interacts’, ‘drug’),(‘drug’, ‘interacts’, ‘gene’),(‘drug’, ‘treats’, ‘disease’)]
g.num_nodes()	hg.num_nodes(ntype)	返回图中节点的数量	4
g.num_edges()	hg.num_edges(etype)	返回图中边的数量	5
g.num_src_nodes()	hg.num_src_nodes(ntype)	返回图中源节点的数量	4
g.num_dst_nodes()	hg.num_dst_nodes(ntype)	返回图中汇节点的数量	4
g.nodes()	hg.nodes(ntype)	返回节点id列表	tensor([0, 1, 2, 3])
g.edges()	hg.edges(etype)	返回边，以(u,v)形式	(tensor([0, 0, 0, 1, 2]), tensor([1, 2, 3, 3, 1]))
g.edges(form=‘all’)	边的起始，结束节点，边的ID	(tensor([0, 0, 0, 1, 2]), tensor([1, 2, 3, 3, 1]), tensor([0, 1, 2, 3, 4]))
g.srcnodes()	hg.srcnodes(ntype)	源节点id列表	tensor([0, 1, 2, 3])
g.dstnodes()	hg.dstnodes(ntype)	汇节点id列表	tensor([0, 1, 2, 3])
g.has_nodes(vid)	hg.has_nodes(vid, ntype)	是否含有某节点，vid为节点的id	True
g.has_edges_between(u,v)	hg.has_edges_between(u,v,etype)	是否含有某边	tensor([False, False])
g.edge_ids(u,v)	hg.edge_ids(u,v,etype)	返回两端点之间边的id	g.edge_ids(0,1)->0
g.find_edges(eid[,etype]		返回该边的两端点	g.find_edges((4, 2))->(tensor([2, 0]), tensor([1, 3]))
g.in_edges(v)	hg.in_edges(v,etype)	该节点的输入边	g.in_edges(1)->(tensor([0, 2]), tensor([1, 1]))
g.out_edges(u)	hg.out_edges(u,etype)	该节点的输出边
g.in_degrees(v)	hg.in_degrees(v,etype)	入度	g.in_degrees(1)->2
g.out_degrees(u)	hg.out_degrees(u,etype)	出度

2.2 关于图的类型

–	hg.is_unibipartite	是否是二分图	False
g.is_multigraph	hg.is_multigraph	是否是多关系图	False
g.is_homogeneous	hg.is_homogeneous	是否是同质图	True

• 二分图 unibipartite
  图中节点属性可以分为两类SRC与DST，使得所有边均为SRC中节点指向DST中节点

• 多关系图 multigraph
  多关系图指同一对节点间有多个边，称为并行边parallel edges，对于同质图，只意味着边的两端节点相同，对于异质图，还意味着边的类型相同，即规范边相同

2.3 关于图特征的属性

g.ndata[fea_name]=tensor	hg.nodes[ntype].data[fea_name]=tensor	创建特征/data
g.edata[fea_name]=tensor	hg.edges[etype].data[fea_name]=tensor	创建特征/data
g.ndata	hg.nodes[nodes].data	返回节点data字典	{‘n_fe’: tensor([[1., 1., 1.],…]), ‘n_fe_matrix’: tensor([[[0.9555, 0.1653]…]])}
g.edata	hg.edges[etype].data	返回边data字典	{‘e_fe’: tensor([[0., 0., 0., 0., 0.]…}
g.srcdata	源节点data
g.dstdata	汇节点data

图特征的切片操作：

g.ndata[‘x’]=th.randn(10,3)	对所有节点赋特征值
g.ndata[‘x’][0]=th.zeros(1,3)	对单个节点赋特征值
g.ndata[‘x’][[0,5,6]]=th.zeros(3,3)	对多个节点赋特征值
g.ndata[‘x’][th.tensor([0, 5, 6])]=th.randn(3,3)	对多个节点赋特征值
g.edata[‘w’]=th.randn(9, 2)	对所有边赋特征值
g.data[‘w’][1]=th.randn(1,2)	对单个边赋特征值
g.edata[‘w’][[0,5,6]]=th.randn(3,2)	对多个边赋特征值
g.edata[‘w’][th.tensor([0,5,6])]=th.randn(3,2)	对多个边赋特征值

2.4 数据类型

DGL可使用int32或着int64类型存储节点和边的ID。节点和边ID的数据类型应当一致。

ID数据类型	node和edge的个数上限
int32	$2^{31}-1$
int64	$2^{63}-1$

节点数较小时，应使用int32类型，因其可以有更快的速度和更小的存储空间

指定，转换与查看ID的数据类型

查看数据类型	g.idtype	torch.int64(默认)
指定	g = dgl.graph(edges, idtype=torch.int32)
变换为int64	g64 = g.long()
变换为int32	g32 = g.int()

1.3.5 邻接与指示矩阵

DGLGraph.adj([transpose, ctx, scipy_fmt, etype])	返回指定类型边的邻接矩阵
DGLGraph.inc(typestr[, ctx, etype])	返回指定边类型的指示矩阵