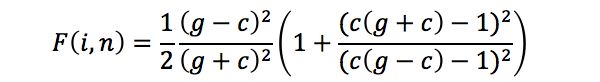原文链接:https://blog.uwa4d.com/archives/1582.html
在上次介绍的微表面模型文章中,我们曾提到过模型中有一个模拟物体表面反射高光的函数 Rs 。在该函数中,有一个表示微表面法线方向分布情况的函数 D(Microfacet Distribution function)。基于对材质表面的观察,许多研究者提出了该分布函数的模型,比较著名的有 Beckmann(1) 以及 Blinn Phong。但是,目前在各种游戏引擎中使用最多的、同时也是效果最好的是一个叫做 GGX 的模型。研究过 PBR 渲染管线的同学可能会经常在各种技术文章中看到 GGX 这个符号。今天我们介绍的这篇论文来自于2007年著名的图形学会议EGSR(Eurographics Symposium on Rendering),而 GGX 也正是首次在这篇文章中提出。
这篇论文的题目是《 Microfacet Models for Refraction through Rough Surfaces 》,它所解决的问题是,如何将微表面反射模型推广到表面粗糙的半透明材质,从而能够模拟类似于毛玻璃的粗糙表面透射效果。同时,文章作者提出了一种新的微表面分布函数 GGX 。并且,通过与前人提出的模型以及真实测量数据做对比,证明 GGX 能够更好地拟合真实测量数据,比前人提出的模型更加精确。
虽然在这篇论文中 GGX 被用来渲染表面粗糙的半透明物体,但是 GGX 作为一种描述微表面法线方向分布的函数,同样适用于渲染表面粗糙的不透明物体。例如在著名的游戏引擎Unity和UE4中,GGX 就被用于渲染不透明物体。下图(2)展示的是UE4引擎的渲染PBR结果,其中微表面分布函数采用的就是 GGX 。
接下来我们介绍这篇论文的内容。首先,我们来介绍这篇论文的渲染效果图,如下图所示:
图中渲染的是一个半透明的球体,该球体表面既有光滑部分也有粗糙的部分。透过光滑表面可以清晰地观察到背景图中不同颜色的条状纹理,而透过粗糙表面则纹理的形状和边界变得比较模糊。同时,可以看到在球的顶端出现了高亮反射的现象,这是由于球面对顶部光源的反射造成的。因此,通常在渲染既有反射又有透射的情况时,我们通常采用BSDF(Bidirectional Scattering Distribution Function)来模拟。这篇论文中的BSDF既包含了反射模型BRDF(Bidirectional Reflectance DistributionFunction)又包含了透射模型BTDF(Bidirectional Transmission Distribution Function)。接下来,我们先介绍这篇论文的BSDF以及其中包含的各项函数,然后介绍论文与前人提出的方法的对比试验。有兴趣的读者可以选择继续阅读,或者直接跳转到后面结果部分,查看论文的更多渲染结果。
一、论文BSDF介绍
给定物体表面某一点的法线方向 n ,入射光方向 i ,以及出射光方向 o ,则该物体表面材质的 BSDF 可以表示为 BRDF 和 BTDF 之和:
其中,fr (i,o,n) 表示 BRDF ,ft (i,o,n) 表示 BTDF 。对于 BRDF ,论文采用了 Cook-Torrance 模型的形式:
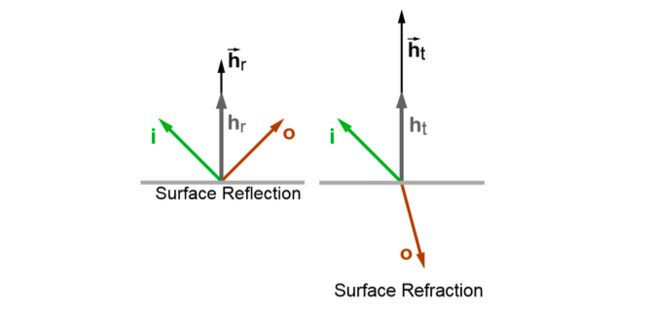
唯一不同的是,论文作者将 Cook-Torrance 模型公式中分母的 π ,改成了常数 4 。论文中的解释是,函数 D 用了不同于Cook-Torrance模型的归一化。其中,hr 表示入射方向 i 和出射方向 o 的中间向量:hr = Sign ( i ∙ n )( i + o )。对于理想镜面反射,hr 方向即为反射点的法线方向。
为了将微表面模型从 BRDF 推广到 BTDF ,论文定义了折射情况下的 ht 。如上图所示,给定折射面两边介质相对密度ηi 和 ηo ,则中间向量可以表示为:
其中,当该情况为理想折射时,ht 与法线方向相同。
根据论文中的公式推导(有兴趣的读者可以查看原论文推导过程),BTDF 可以表示为:
由上述公式可以看到,论文中定义的 ft 与 Cook-Torrance 模型中的fr 有相似的形式。其中,都包含了模拟菲涅尔现象的函数 F ,模拟微表面法线方向分布的函数 D ,以及阴影遮挡函数 G 。接下来,我们将逐一介绍 BTDF 中这些函数的定义。
二、F、G、D 函数的具体形式
首先,我们介绍菲涅尔项 F 。论文作者采用了与 Cook-Torrance 模型中类似的菲涅尔项表达式:
其中,c =|i ∙ n|。与Cook-Torrance模型不同的是,g 被定义为与介质密度相关的函数:
当内部全反射发生时,F =1。
对于阴影遮挡函数G,论文作者采用了与 Cook-Torrance 模型不一样的函数:Smith shadowing-masking3。该函数依赖于微表面法向分布函数 D ,最初它是用来计算高斯分布的阴影遮挡,后来被推广到任意的分布函数。Smth G 函数用两个子函数的的积来近似:
其中,G1 是根据微表面法向分布函数 D 推导出来(有兴趣的同学可以从原文查看具体推导过程)。
最后,我们介绍 GGX 微表面法向分布函数 D,以及对应的 G1 函数。在介绍分布函数 D 之前,我们先介绍微表面模型中的微观法线以及宏观法线的概念。由于微表面模型假设物体表面是由许多凹凸不平的微小平面构成,因此这些微小平面的法线与物体表面的法线并不相同。
如上图所示,n 表示物体表面宏观法线方向,也就是我们通常在渲染中用到的物体表面法线方向。m 表示看不见的微小平面的法线方向。函数 D 正是描述了 m 的分布情况。不同的 m 的分布,造成了物体表面不同程度的粗糙度。
2.1 GGX 分布函数
若用 ν 表示任意方向,θm 表示 m 与n 之间的夹角,θv 表示 ν 与 n 之间夹角,αρ 表示控制变量。则 GGX 分布函数 D ,以及阴影遮挡函数 G1 可以表示为:
其中,Χ+ (α)表示阶跃函数,当 α > 0 时取值 1,当 α ≤ 0 取值 0。论文比较了Beckmann1、Phong以及 GGX 分布函数以及阴影遮挡函数在不同控制变量取值时的曲线,如下图所示:
其中,Beckmann 、Phong 以及 GGX 分别用红色、蓝色和绿色线表示。从图中可以看到,Beckmann 与 Phong 分布函数曲线几乎完全重合,GGX 则更窄拖尾更长。
上图是Unity引擎的渲染结果4。其中,左边是 GGX 分布函数渲染结果,右边是 Phong 分布函数渲染结果。在 GGX 的结果中,高光的衰减拖尾更长,视觉上周围泛光的范围更广一些,更加符合实际的反射高光情形。
三、与真实采集数据比较
论文作者利用前人提出的方法,从真实半透明材质中采集了光线透射的数据。然后,分别用 Beckmann1 以及 GGX 的分布函数的 BTDF 进行拟合。论文作者采集了四组数据,ground、frosted、etched 以及 antiglare。其中,各组数据的控制变量取值如下图所示:
每组数据的拟合曲线如下图所示:
从上至下,从左至右,分别是 ground、frosted、etched、antiglare的数据。黑色点表示真实采集数据,Beckmann1 和 GGX 曲线分别用红色和绿色表示。从上面的曲线可以看到,GGX 曲线(绿色)更加贴近真实采集数据。
四、更多渲染结果展示
论文作者通过真实数据拟合的模型控制参数渲染了粗糙表面半透明的结果,并达到了比较好的渲染效果,如下图所示:
其中,左图是用Beckmann1分布函数以及 antiglare 数据参数渲染的结果,中间和右边图是分别用 ground 和 etched 数据参数以及 GGX 分布函数渲染的结果。
五、总结
这篇论文将 Cook-Torrance 模型从模拟粗糙表面反射推广到粗糙表面的透射情况。并且,提出了一个新的微表面分布函数 GGX 。通过对真实采集数据的拟合以及与前人提出的分布函数比较,GGX函数能够更好地拟合真实数据。
六、论文信息
作者介绍:
Bruce Walter,康奈尔大学博士毕业,康奈尔大学计算机图形学研究员
Stephen R. Marschner,康奈尔大学博士毕业,康奈尔大学教授
Hongsong Li,北京理工大学,光学专业毕业,光学专家
Kenneth E. Torrance,著名计算机图形学学者,曾经在康奈尔大学机械与航天工程学院工作,目前已退休。
下载链接:
http://www.cs.cornell.edu/~srm/publications/EGSR07-btdf.html
参考文献:
【1】 P.Beckmann and A. Spizzichino, The Scattering of Electromagnetic Waves from Rough Surfaces, Pergamon Press, New York 1963.
【2】 http://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_notes_v2.pdf
【3】 K.E.Torrance, E. M. Sparrow : Theory for off-specular reflection from roughened surfaces. Journal of Optical Society of America 57, 9(1967), 1105–1114.
【4】 https://blogs.unity3d.com/cn/2016/01/25/ggx-in-unity-5-3/
这是侑虎科技第203篇原创文章,欢迎转发分享,未经作者授权请勿转载。如果您也有任何独到的见解或者全新的发现也欢迎联系我们,一起探讨。(QQ群465082844)
关于惟学无际
【惟学无际】是UWA在2017年推出的全新研究型专栏,我们将为大家推荐极具实际价值的学术论文,并梳理其中的研究背景、实现原理和执行方法等。内容专注于游戏、VR和AR相关的计算机图形学领域。正所谓问渠哪得清如许,为有源头活水来 ,希望大家在研发的过程中不仅知其然,还能知其所以然。