FPGA数字系统设计(8)——可综合电路及状态机
一、可综合电路
行为级可综合语法和数据流级语法合在一起被称为RTL级,该级别的模型是可以被综合成电路进而实现的。
1、module 和endmodule 作为模块声明的关键字,必然是可以被综合的。
2、输入input,输出output和双向端口inout的声明是可以被综合的。
3、变量类型reg、wire、integer都是可以被综合的。
4、参数parameter和宏定义define是可以被综合的。
5、所有的Verilog HDL 内建门都是可以使用的。
6、数据流级assign语句是可以被综合的。
7、行为级中敏感列表支持电平和边沿变化,类似posedge、negedge都是可以被综合的。
8、always、funtion是可被综合的,task中若不含延迟也是可被综合的。
9、顺序快begin···end可以被综合
10、if 和case语句可被综合
Verilog HDL中不可被综合的语法如下所示
1、初始话initial结构不可被综合,电路中不会存在这样的单元。电路中一旦通电就会自动获得初始值,除此以外时序电路可以用复位端完成初始化组合电路不需要初始化。
2、#带来的延迟不可综合,电路中同样不会出现这样简单的延迟电路,所有的延迟电路都要通过计时电路或交互信号来完成
3、并行块fork···join不可综合,并行块的语义在电路中不能被转化。
4、用户自定义原语UP不可被综合
5、时间变量time和实数变量real不能被综合
6、wait、event、repeat、forever等行为级语法不可被综合。
7、一部分操作符可能不会被综合,例如除法/操作和求余%操作
二、应用实例(移位除法器器模型)
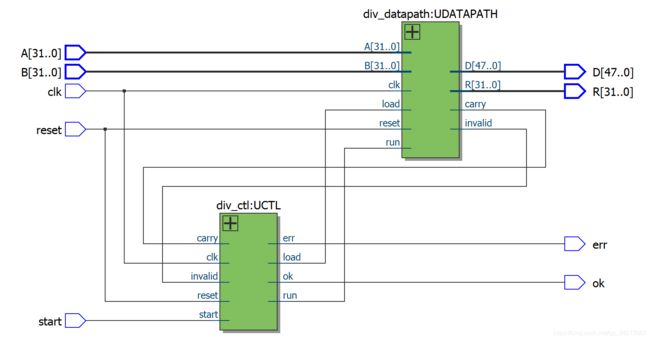
移位除法器的模型,采用的算法类似于笔算除法,只是变为二进制而不是十进制,由于代码较长,采用层次化的方式进行设计,同时采用循环迭代的方式使用一个电路模块反复运算得到最后的结果。该模块的设计违背了流水的设计,但是大大的减少了面积,时间上会有相应延长。
//div的顶层代码,其中包含两个子模块,分别是div_ctl用来生成控制信号,div_datapath用来进行迭代计算
module div (clk, reset, start, A, B, D, R, ok, err);
parameter n = 32;
parameter m = 16;
input clk, reset, start;
input [n-1:0] A, B;
output [n+m-1:0] D;
output [n-1:0] R;
output ok, err;
wire invalid, carry, load, run;
div_ctl UCTL(clk, reset, start, invalid, carry, load, run, err, ok);//控制信号
div_datapath UDATAPATH(clk, reset, A, B, load, run, invalid, carry, D, R);//计算迭代信号
endmodule //子模块生成控制信号
module div_ctl(clk, reset, start, invalid, carry, load, run, err, ok);
parameter n = 32;
parameter m = 16;
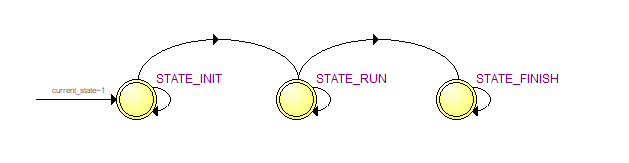
parameter STATE_INIT = 3'b001;
parameter STATE_RUN = 3'b010;
parameter STATE_FINISH = 3'b100;
input clk, reset, start, invalid, carry;
output load, run, err, ok;
reg load, run, err, ok;
reg [2:0] current_state, next_state; //当前标志,下一个标志
reg [5:0] cnt; //迭代次数标志
always @(posedge clk or negedge reset)begin
if(!reset)begin
current_state <= STATE_INIT;
cnt <= 0;
end
else begin
current_state <= next_state;
if (run) cnt <= cnt + 1'b1;
end
end
always @(posedge clk or negedge reset)begin
if(!reset)begin
err = 0;
end
else if(next_state == STATE_RUN)begin
if(invalid) err <= 1;
end
end
always @(current_state or start or invalid or carry or cnt)begin
load <= 1'b0;
ok <= 1'b0;
run <= 1'b0;
case (current_state)
STATE_INIT:
begin
if(start) next_state <= STATE_RUN;
else next_state <= STATE_INIT;
load <= 1;
end
STATE_RUN:
begin
run <= 1;
if(invalid) begin
next_state <= STATE_FINISH;
end
else if(cnt == (n+m-1))begin //迭代47次
next_state <= STATE_FINISH;
end
else begin
next_state <= STATE_RUN;
end
end
STATE_FINISH:
begin
ok <= 1;
next_state <= STATE_FINISH;
end
default:
begin
next_state <= STATE_INIT;
end
endcase
end
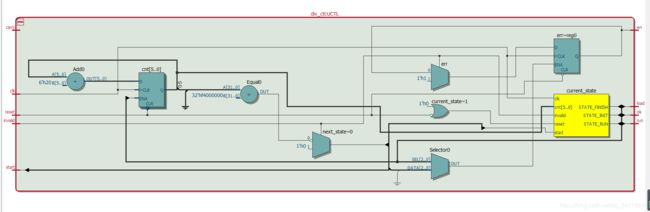
endmodulediv_path RTL电路
//子模块div_dataphth,用来迭代计算
module div_datapath(clk, reset, A, B, load, run, invalid, carry, D, R);
parameter n = 32;
parameter m = 16;
input load, run, clk, reset;
input [n-1:0] A, B;
output invalid, carry;
output [n+m-1:0] D;
output [n-1:0] R;
reg carry;
reg [n+n+m-2:0] R0;
reg [m+n-1:0] D;
reg [n-1:0] B0;
wire invalid,CO;
wire [n-1:0] DIFF, R;
assign R = {
carry, R0[n+n+m-2:n+m]};
assign invalid = (B0 == 0);
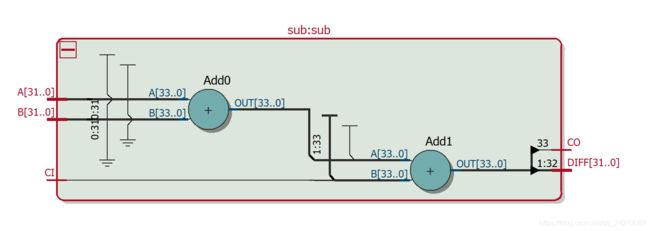
sub sub(R0[n+n+m-2:n+m-1], B0, 1'b0, DIFF, CO);//实例化减法器
always @(posedge clk)begin
if(load)begin //初始阶段
D <= 0;
R0 <={
{(n-1){1'b0}}, A, {
m{
1'b0}}};
B0 <= B;
carry <= 1'b0;
end
else if(run)begin //结束阶段
if(CO && !carry)begin
R0 <= {
R0, 1'b0};
D <= {D[n+m-2:0], 1'b0};
carry <= R0[n+n+m-2];
end
else begin //迭代阶段
R0 <= {
DIFF, R0[n+m-2:0], 1'b0};
D <= {D[n+m-2:0], 1'b1};
carry <= DIFF[n-1];
end
end
end
endmodulemodule sub(A, B, CI, DIFF, CO);
parameter n = 32;
input [n-1:0] A, B;
input CI;
output CO;
output [n-1:0] DIFF;
assign {
CO,DIFF} = {
1'b0, A} - {1'b0, B} - {
{
n{
1'b0}}, CI};
endmodule仿真电路图如下图所示
三、状态机
1、状态机的简介
时序逻辑电路的设计核心在于如何在时钟的的控制下完成多种状态的变化,有数字电路的知识可知,时序电路的变化会遵循状态转换图,把状态转换图变为代码模块就可以编写成有限状态机。
有限状态机适合设计程序复杂但具有一定规律性的逻辑结构,有限状态机也常被缩写为FSM(Finite State Machine)。在使用有限状态机进行电路设计时,设计者要先根据所涉及的电路情况画好状态转换图,确认每个状态的输入/输出转换关系,然后依照状态机来编写代码。
有限状态机分为moore型和mealy型两种,也称为摩尔型和米利型。
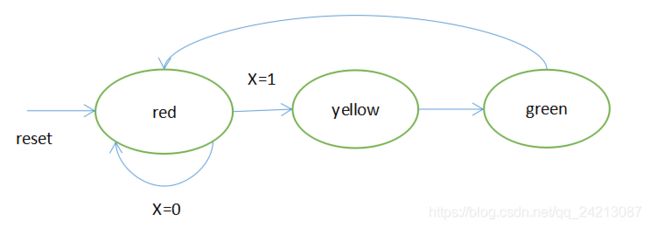
moore型状态机的输出仅仅与当前状态有关,如下图所示
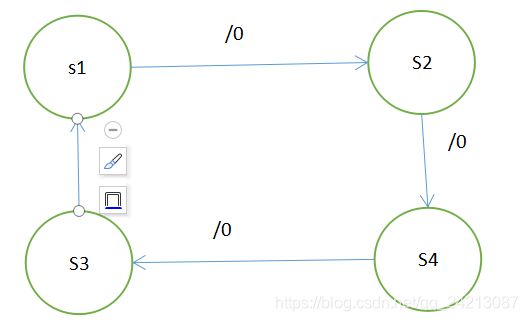
mealy型状态机的输出不仅与当前状态有关,还与当前输出有关,如下图所示:
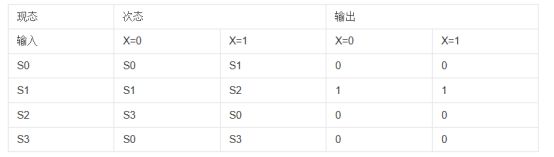
状态表如下图所示
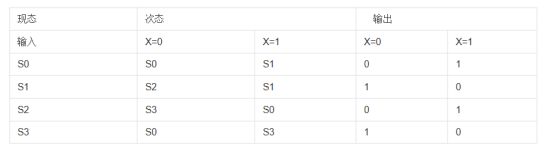
2、两种红绿灯电路的状态机模型
2.1Moore型红绿灯
状态图如图所示
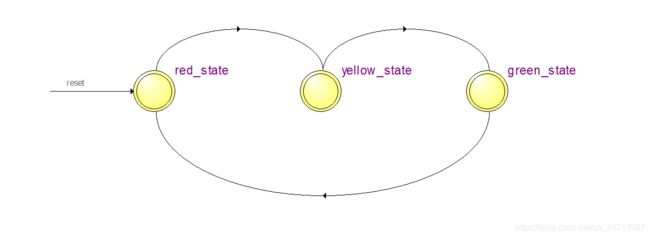
module trafficlight1(clock, reset, red, yellow, green);
input clock, reset;
output red, yellow, green;
reg red, yellow, green;
reg [1:0] current_state, next_state;
parameter red_state = 2'b00;
parameter yellow_state = 2'b01;
parameter green_state = 2'b10;
parameter delay_red = 4'd8;
parameter delay_yellow = 4'd3;
parameter delay_green = 4'd11;
always @(posedge clock or posedge reset)begin
if(reset)
begin
current_state <= red_state;
end
else
begin
current_state <= next_state;
end
end
always @(current_state)begin
case (current_state)
red_state:begin
red = 1;
yellow = 0;
green = 0;
repeat (delay_red) @(posedge clock);
next_state = yellow_state;
end
yellow_state:begin
red = 0;
yellow = 1;
green = 0;
repeat(delay_yellow)@(posedge clock);
next_state = green_state;
end
green_state:begin
red = 0;
yellow = 0;
green = 1;
repeat(delay_green)@(posedge clock);
next_state = red_state;
end
default:begin
red = 1;
yellow = 0;
green = 0;
repeat (delay_red)@(posedge clock);
next_state = red_state;
end
endcase
end
endmodule
//mealy型状态机红绿灯
module trafficlight(clock, reset, red, yellow, green, cnt);
input clock, reset, cnt;
output red, yellow, green;
reg red, yellow, green;
reg [1:0] current_state, next_state;
parameter RED_STATE = 2'b00,
YELLOW_STATE = 2'b01,
GREEN_STATE = 2'b10,
delay_red = 4'd8,
delay_yellow = 4'd3,
delay_green = 4'd11;
always@(posedge clock or posedge reset)begin //原态和新态的转换
if(reset)
begin
current_state = RED_STATE;
end
else
begin
current_state = next_state;
end
end
always @(current_state, cnt)begin //当current_state 和cnt 变化后进行判断
case(current_state)
RED_STATE:
begin
red = 1;
yellow = 0;
green = 0;
if (cnt == 1 )
begin
repeat (delay_red)@(posedge clock);
next_state = YELLOW_STATE;
end
end
YELLOW_STATE:
begin
red = 0;
yellow = 1;
green = 0;
repeat (delay_yellow)@(posedge clock);
next_state = GREEN_STATE;
end
GREEN_STATE:
begin
red = 0;
yellow = 0;
green = 1;
repeat (delay_green)@(posedge clock);
next_state = RED_STATE;
end
default:
begin
red = 1;
yellow = 0;
green = 0;
next_state = RED_STATE;
end
endcase
end
endmodule
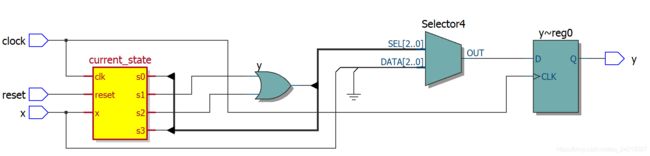
3、一段式状态机
这里应用一个序列检测电路来说明。模块中只包含一个always语句,用来检测输入的数值,当数值为0110时,标志检测成功。此时通过输出端输出一个信号,用来与之后的电路进行交互。
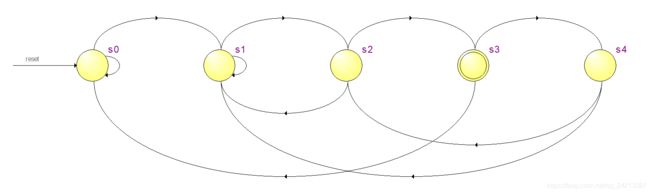
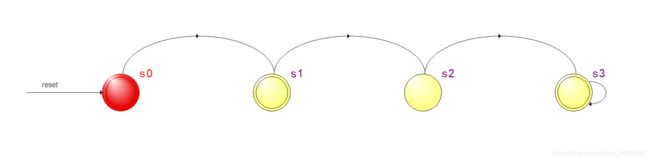
状态图如下图所示
module fam_seq1(clock, reset, x, z);
input reset, clock;
input x;
output z;
reg z;
reg [2:0] state;
parameter s0 = 3'd0,
s1 = 3'd1,
s2 = 3'd2,
s3 = 3'd3,
s4 = 3'd4;
always@(posedge clock or posedge reset)begin
if (reset)
begin
state <= s0;
z <= 0;
end
else
begin
casex(state)
s0:begin
if(x == 1)
begin
state <= s0;
z <= 0;
end
else
begin
state <= s1;
z <= 0;
end
end
s1:begin
if(x == 0)
begin
state <= s1;
z <= 0;
end
else
begin
state <= s2;
z <= 0;
end
end
s2:begin
if(x == 0)
begin
state <= s1;
z <= 0;
end
else
begin
state <= s3;
z <= 0;
end
end
s3:begin
if(x == 0)
begin
state <= s4;
z <= 1;
end
else
begin
state <= s0;
z <= 0;
end
end
s4:begin
if(x == 0)
begin
state <= s1;
z <= 0;
end
else
begin
state <= s2;
z <= 0;
end
end
default:begin
state <= s0;
end
endcase
end
end
endmodule仿真图

一段式状态机的特点
(1) 仅有一段always结构,里面包含了状态转换、复位和输出。
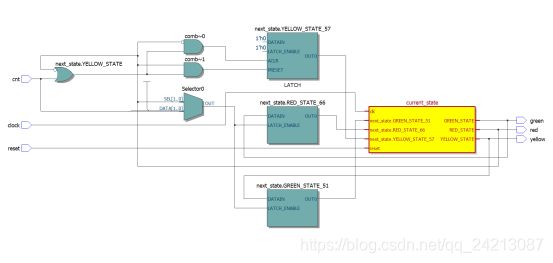
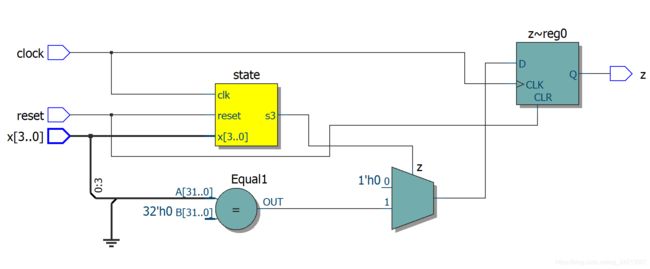
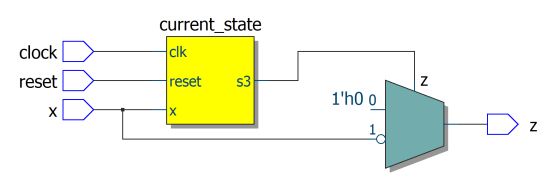
(2)always结构的敏感列表是时钟沿,所以最后的输出结构是以寄存器形式输出的,既是时序逻辑输出,可以参考RTL电路图,最后一级的输出来自寄存器。
但是由于一个always结构中包含了所有的描述语句,再进行后期维护时不方便,如要修改或添加几个状态,改变一些输出等,可以把这个always结构中的一些语句单独提炼出来使其更具有可维护性和可读性 。
4、两段式状态机
同样是使用序列检测的模型进行两段式状态机的编写
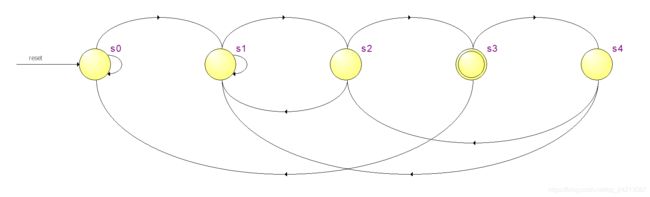
状态图如图所示:
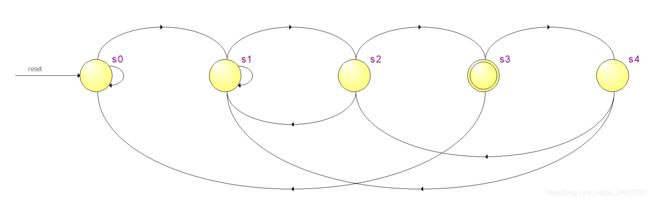
module fam_seq2(clock, reset, x, z);
input clock, reset, x;
output z;
reg z;
reg [2:0] current_state, next_state;
parameter s0 = 3'd0;
parameter s1 = 3'd1;
parameter s2 = 3'd2;
parameter s3 = 3'd3;
parameter s4 = 3'd4;
always@(posedge clock or posedge reset)begin//原态和新态之间的转换
if (reset)
begin
current_state <= s0;
end
else
begin
current_state <= next_state;
end
end
always@(current_state or x)begin //指定状态的变换,注意@(current_state or x)
casex (current_state)
s0:begin
if(x == 1)
begin
next_state <= s0;
z <= 0;
end
else
begin
next_state <= s1;
z <= 0;
end
end
s1:begin
if(x == 0)
begin
next_state <= s1;
z <= 0;
end
else
begin
next_state <= s2;
z <= 0;
end
end
s2:begin
if(x == 0)
begin
next_state <= s1;
z <= 0;
end
else
begin
next_state <= s3;
z <= 0;
end
end
s3:begin
if(x == 1)
begin
next_state <= s0;
z <= 0;
end
else
begin
next_state <= s4;
z <= 1;
end
end
s4:begin
if(x == 0)
begin
next_state <= s1;
z <= 0;
end
else
begin
next_state <= s2;
z <= 0;
end
end
endcase
end
endmodule仿真图如下图所示

5、三段式状态机
仍然使用时序检测,只是将电路的输出与状态的转换分开,构成第三段
module fam_seq3(clock, reset, x, z);
input clock, reset, x;
output z;
reg z;
reg [2:0] current_state, next_state;
parameter s0 = 3'd0;
parameter s1 = 3'd1;
parameter s2 = 3'd2;
parameter s3 = 3'd3;
parameter s4 = 3'd4;
always@(posedge clock or posedge reset)begin //原态和新态之间的转换
if (reset)
begin
current_state <= s0;
end
else
begin
current_state <= next_state;
end
end
always@(current_state or x)begin //指定新态的变化
casex (current_state)
s0:
begin
if(x == 1)
begin
next_state = s0;
end
else
begin
next_state = s1;
end
end
s1:
begin
if(x == 0)
begin
next_state = s1;
end
else
begin
next_state = s2;
end
end
s2:
begin
if(x == 0)
begin
next_state = s1;
end
else
begin
next_state = s3;
end
end
s3:
begin
if(x == 1)
begin
next_state = s0;
end
else
begin
next_state = s4;
end
end
s4:
begin
if(x == 0)
begin
next_state = s1;
end
else
begin
next_state = s2;
end
end
default
begin
next_state = s0;
end
endcase
end
always@(current_state or x)begin //制定不同状态下的输出
case(current_state)
s0: z = 0;
s1: z = 0;
s2: z = 0;
s3:
begin
if (x == 0)
z = 1;
else
z = 0;
end
s4: z = 0;
default: z = 0;
endcase
end
endmodule 三段式状态机的形式比较固定,
第一段always用来完成原态和新态的转换,
第二段always用来完成确定新态的变化情况,
第三段always用来描述不同情况下的输出。
其中第一段是对时钟信号边沿敏感的,即使用时序逻辑电路,采用非阻塞赋值
第二段是对current_state或x敏感的,使用的是组合逻辑电路,采用的的是阻塞赋值,一般使用case语句和if语句完成输入值确定新态的过程。
但是第三段的问题较多,可以有五种信号的敏感而产生不同的输出情况。
6、三段式状态机第三段的仿真分析
对不同的信号敏感产生不同的输出情况
1、 always @(current_state or x)
if (current_state == xxx and x == yyy)
2、always@(current_state)
3、always@(next_state)
4、always@(posedge clock)
case(current_state)
5、always@(posedge_clock)
case(next_state)接下来针对不同的情况分别分析2、3、4、5这四种情况
always@(current_state)begin //制定不同状态下的输出
case(current_state)
s0: z = 0;
s1: z = 0;
s2: z = 0;
s3: z = 0;
s4: z = 1;
default: z = 0;
endcase
endalways@(next_state)begin //制定不同状态下的输出
case(next_state)
s0: z = 0;
s1: z = 0;
s2: z = 0;
s3: z = 0;
s4: z = 1;
default: z = 0;
endcase
endalways@(posedge clock)begin //制定不同状态下的输出
case(current_state)
s0: z <= 0;
s1: z <= 0;
s2: z <= 0;
s3: z <= 0;
s4: z <= 1;
default: z <= 0;
endcase
endalways@(posedge clock)begin //制定不同状态下的输出
case(next_state)
s0: z <= 0;
s1: z <= 0;
s2: z <= 0;
s3: z <= 0;
s4: z <= 1;
default: z <= 0;
endcase
end
五种第三段的写法在实际电路中的变化过程
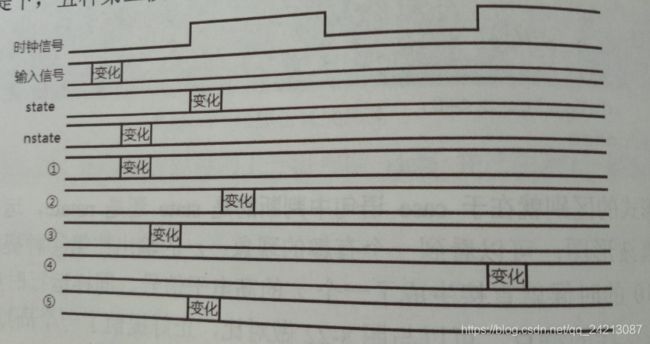
①always@(state or x)——这种形式当输入信号稳定且state稳定时就会产生输出,所以输出开始变化的位置和nstate应该是一样的,因为nstate也是等待输入稳定后就开始变成所需状态。换言之,输出信号会在clk上升沿之前产生。如果后级电路使用这个输出作为使能位,那前后级电路之间可以完成无缝对接。
②always@(state)——这种形式需要等到state发生变化时才能产生输出,state受时钟上升沿控制,变化稳定后产生有效的输出,参考图中输出②的位置,此时这个信号会在下一个周期时被后级电路使用,从而使后级电路的工作过程滞后一个周期。
③always@(nstate)——因为nstate的变化就发生在clk上升沿之前,所以当nstate稳定后,输出端的变化就开始了,知道最后产生一个稳定输出为止。只要时钟周期设计合理,这个输出也可以被即将到来的clk上升沿收集到,并在下一级电路中使用,所以效果和①相似,而采用③的方式时如果nstate变化较慢,也可能退后一个时钟周期。
④always@(posedge clk) + case(state)——因为state要等到上升沿
时才能开始变化,所以在第一个clk上升沿时产生的输出依然是上一个state情况,因为新的state还没有开始变化,等到第二个clk上升沿时产生的才是有效的输出,这个输出也会滞后一个周期,但是优点是受时钟控制,输出电路部分是时序电路,即最后的输出也是通过寄存器输出的,在时序电路中比较容易控制。
⑤always@(posedge clk) + case(nstate)——由于nstate在时钟上升沿之前就稳定了,所以如果case语句中对nstate进行判断,则输出变化的位置就是第一个clk的上升沿,如图所示。clk上升沿到来时,一方面state发生变化,另一方面输出值发生变化,既保证了信号的同步,也使用了时序电路作为输出。
Moore型状态机的第三段变化输出情况
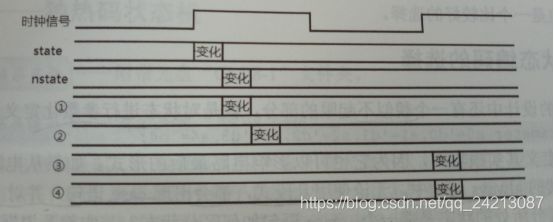
①always@(state)——这种情况下输出会在state稳定后开始进行有效地输出变化,所以会发生在第一个clock边沿之后,如果是级联电路,本级电路进入到当前状态,下一级电路需要在一个时钟周期能接收到本级电路产生的输出信号。
②always@(nstate)——这种情况下输出信号产生依赖与nstate,所以会比①中变化的位置更慢一些,如果按这种情况在本时钟周期内到达稳定,输出信号也会被后级电路在一个周期接收到。
③always@(posedge clk) + case(state)——这种形式的好处是在于输出受时钟控制,但是case语句检测的是state,所以会在下一个时钟周期便演出产生输出,作为本级电路的输出信号没有问题,但是如果要和后级电路产生链接,需要在时序方面做好处理,因此此时后级电路可能需要再延迟一个时钟周期才能相应本级电路的输出
④always@(posedge clk) + case(nstate)——这种方式和mealy型类似,一方面可以产生时序电路输出,另一方面由case语句检测的是nstate,所以在下一个时钟信号来临时,一方面受第一段always控制,完成state<=nstate的赋值,state变为新态,另一方面输出也有nstate决定,所以产生的输出就是当前state的输出值。
四、应用实例
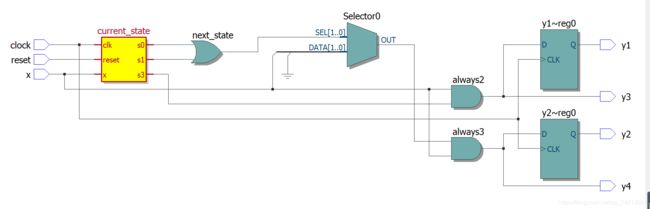
1、独热码状态机
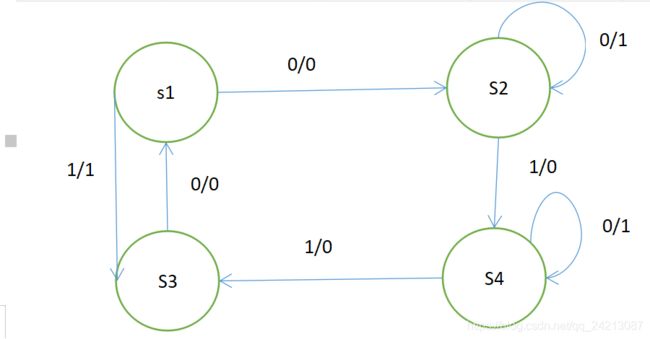
状态图
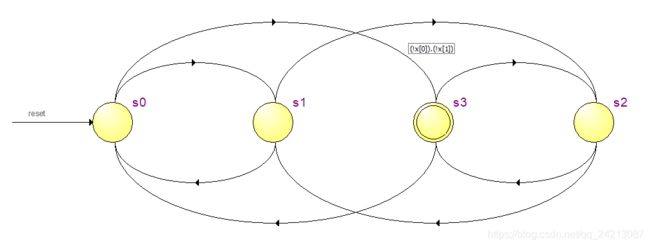
module one_hot_code(clock, reset, x, y);
input clock, reset;
input x;
output y;
reg y;
reg [3:0] current_state,next_state;
parameter s0 = 4'b0001;
parameter s1 = 4'b0010;
parameter s2 = 4'b0100;
parameter s3 = 4'b1000;
always@(posedge clock or posedge reset)begin //原态和新态之间转换
if(reset)
begin
current_state <= s0;
end
else
begin
current_state <= next_state;
end
end
always@(current_state or x)begin //指定状态
casex(current_state)
s0:begin
if (x == 1)
begin
next_state = s1;
end
else
begin
next_state = s3;
end
end
s1:begin
if (x == 0)
begin
next_state = s2;
end
else
begin
next_state = s0;
end
end
s2:begin
if (x == 0)
begin
next_state = s3;
end
else
begin
next_state = s1;
end
end
s3:begin
if (x == 0)
begin
next_state = s0;
end
else
begin
next_state = s2;
end
end
default:begin
next_state = s0;
end
endcase
end
always@(posedge clock)begin //指定状态输出
case(current_state)
s0:
begin
if(x == 0)begin
y = 1;
end
else
begin
y = 0;
end
end
s1: y = 0;
s2: y = 0;
s3:
begin
if(x == 0)begin
y = 0;
end
else
begin
y = 1;
end
end
default: y = 0;
endcase
end
endmodulemodule gary_code (clock, reset, x, y1, y2, y3, y4);
input clock, reset, x;
output y1, y2, y3, y4;
reg y1, y2, y3, y4;
reg [1:0] current_state, next_state;
parameter s0 = 2'b00;
parameter s1 = 2'b01;
parameter s2 = 2'b11;
parameter s3 = 2'b10;
always @(posedge clock or posedge reset)begin
if(reset)
begin
current_state = s0;
end
else
begin
current_state = next_state;
end
end
always @(current_state or x)begin
casex(current_state)
s0:
begin
if(x == 1)
next_state = s1;
else
next_state = s0;
end
s1:
begin
if(x == 1)
next_state = s2;
else
next_state = s0;
end
s2:
begin
if(x == 1)
next_state = s3;
else
next_state = s0;
end
s3:
begin
if(x == 1)
next_state = s3;
else
next_state = s0;
end
default:next_state = s0;
endcase
end
always@(posedge clock)begin
if(current_state == s3 && x == 1)
y1 = 1;
else
y1 = 0;
end
always@(posedge clock)begin
if(next_state == s3 && x == 1)
y2 = 1;
else
y2 = 0;
end
always@(current_state)begin
if(current_state == s3 && x == 1)
y3 = 1;
else
y3 = 0;
end
always@(next_state)begin
if(next_state == s3 && x == 1)
y4 = 1;
else
y4 = 0;
end
endmodule