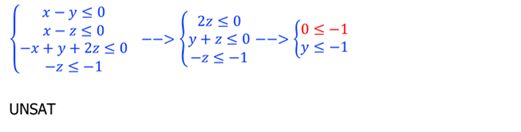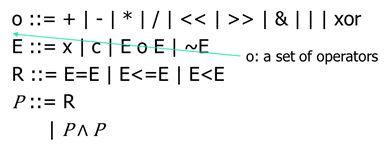2020形式化方法复习笔记
(第二课:数学基础)
1.逻辑基础
命题逻辑 + 谓词逻辑
变体:经典逻辑、构造逻辑。
2.命题逻辑 Propositional logic:
每个形式系统应当包括语法+语义
2.1 语法 The syntax
P ⋁ P P \bigvee P P⋁P :析取
P ⋀ P P \bigwedge P P⋀P:合取
P → P P \to P P→P:蕴含
2.2 证明系统 The proof system
数学上:Hibert系统,构造性,没有规律可言。
CS上:自然演绎系统,具有机械化步骤,即算法。
Nature deduction
-
断言 Judgment:Γ⊢
Γ为命题组成的列表,P是单独的逻辑命题。Example: P, Q, R ⊢
可以理解为Γ是一组假定为真,在这种假定的前提下,能够推出P为真。 -
推理规则
四元组:直线,直线上面为n个断言(前提/假设),下面一个断言(结论),右侧名字(推理规则名字)。

意思是,如果在Γ条件下去证明P,那么只需要证明Γ1⊢1、Γ2⊢2…,同理一旦知道前提条件,即可证明Γ⊢。
由假设到结论,由结论到假设的双向推理过程。
如果当前提中,n=0时,即为公理(axiom)。
(1)直接证明的结论P,已经存在前提条件中。(公理)
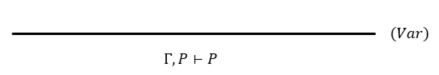
(2)T是无条件成立(公理)
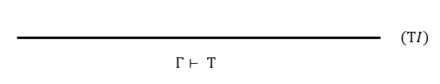
TI中的I为introduction,引入。
(3)⊥,假推出一切!

⊥E中的E为elimination,消去。
从一组自相矛盾的条件出发,任何结论都成立。
(4) ⋀ \bigwedge ⋀,如果可以证明P,也可以证明Q,那么可以证明 P ⋀ P P \bigwedge P P⋀P

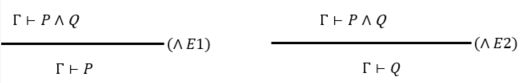
(5) P ⋁ P P \bigvee P P⋁P
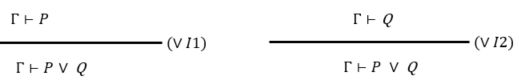

(6) P → P P \to P P→P

(7)¬ (反证法)
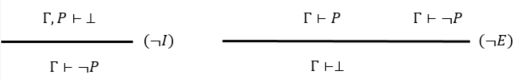
(8)¬¬ 双重否定律
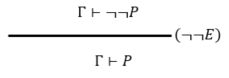
不同的是之前所有都是语法制导。
Proof Tree :注意P是随意产生的还是在原有的命题中的!

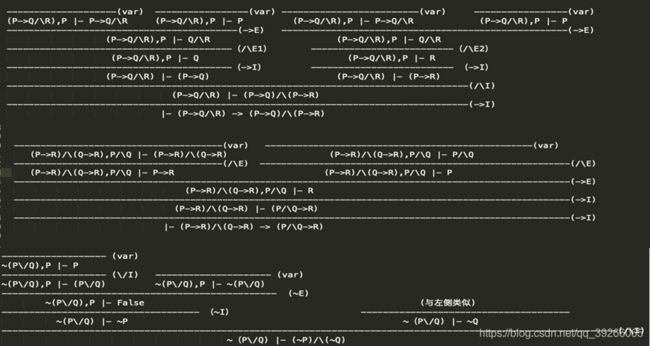
2.3 语义 Semantics
证明系统关心的是是否可证,以及不可证,而在语义学中更关心计算,得到的结果是“真”还是“假”。但并不是所有问题都是可计算的,NP以及NPC问题。
- 真值表 The truth table
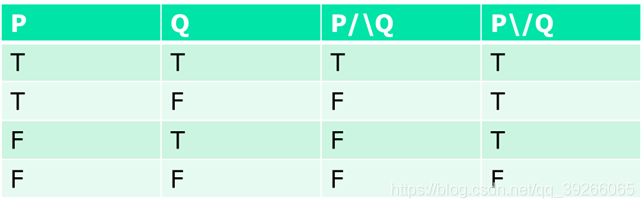
- Interpertation
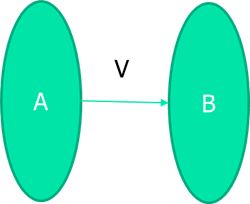
在以上两个形式系统AB中,A即上文中研究的命题逻辑系统(逻辑命题,连接词,推理规则),B即真值表系统(T,F,AND,OR),语义学本质上要写一个编译器V,将A中的元素编译(数学中即映射\函数)到B中。 - 重言式 Tautology (永真式)
即对于任意的编译器V,V(P)=T,使用⊨ P来表示。
(⊢语法上可证,⊨ P通过计算为真)
两种观点命题成立,1.在证明系统中可证 2.在模型论中为真。
可靠性:Γ⊢ P => Γ ⊨ P
完备性:Γ ⊨ P => Γ⊢ P
3.构造逻辑 Constructiove logic
3.1 Motivation
(第三课:命题逻辑)
3.2 The syntax
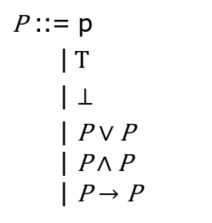
和经典结构的语义相比,没有否定连接词,否定在构造系统中定义成语法糖(并不是必需的)
3.3 证明系统 proof theory (也是基于自然演绎)
3.4 语义学 Semantics(了解,不考)
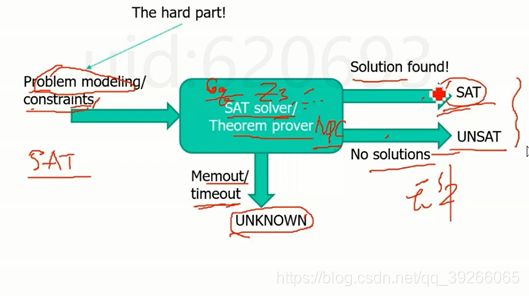
4.Satisiability (SAT问题)
NP问题:存在算法,但是时间复杂度为指数时间,不是现实可行。
NPC问题:其他NP问题都能在多项式时间内转换成NPC问题,只要NPC问题能解,其他问题也可解。
SAT:给定一个命题P,是否存在一个模型(变量的赋值)使得最终P为Ture。
4.1 SAT vs. valid
V a l i d ( P ) ⟺ u n s a t ( P ) Valid(P) \iff unsat(~P) Valid(P)⟺unsat( P)如果证明P为真,只需要证明~P为UNSAT。
4.2 DPLL
P → N N F → C N F P \to NNF \to CNF P→NNF→CNF
范式(1)否定范式 NNF
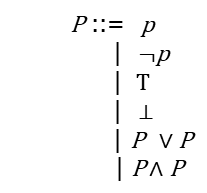
a.没有蕴含 b.所有的否定只能出现在原子命题前
NFF Example
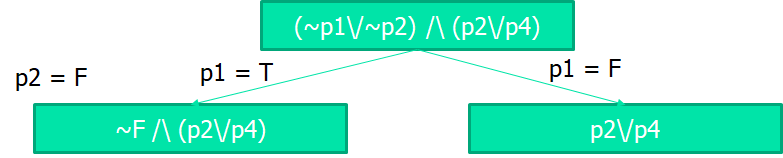
p 1 ⋀ p1 \bigwedge p1⋀~ p 2 ⋀ p 3 ⋀ p2 \bigwedge p3 \bigwedge p2⋀p3⋀~ p 4 p4 p4
Non NFF:
p 1 ⋀ p1 \bigwedge p1⋀~ ( p 2 ⋀ p 3 ) ⋀ (p2 \bigwedge p3)\bigwedge (p2⋀p3)⋀ ~ p 4 p4 p4
消除蕴含规则:
![]()
转换成NFF规则(消去~非原子命题):
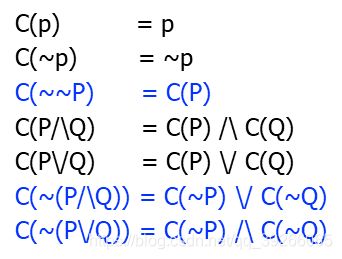
(2)CNF 合取范式

CNF Example
( p 1 ⋁ p 2 ) ⋀ ( p 3 ⋁ p 4 ) (p1 \bigvee ~p2) \bigwedge (p3 \bigvee ~p4) (p1⋁ p2)⋀(p3⋁ p4)
Non CNF:
p 1 ⋀ ( p 2 ⋁ p 3 ) p1 \bigwedge (~p2 \bigvee p3) p1⋀( p2⋁p3) ⋁ \bigvee ⋁ p 4 ~p4 p4
转换成CNF:
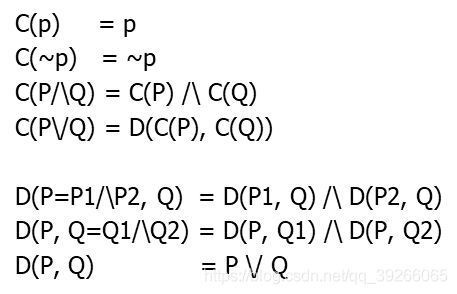
(3)DIMACS standard
如果当一个命题已经满足CNF,那么用数字代表一个命题进行编码。
4.3 DPLL算法改进
(第四课 谓词逻辑)
4.4 Modeling and reasoning with SAT
Example 1:circuit layout

Example 2: seat arrangement
Example 3: n-queens puzzle
Assignment 3 SAT
Part A: Basic Propositional Logic
'''
By default, Z3 only outputs the first row in the truth table:
P Q P\/Q
-----------------
t t t
t f t
f t t
f f f
'''
# then check the satisfiability again. For the above example:
F = Or(P, Q)
solve(F)
F = And(F, Not(And(P, Not(Q))))
solve(F)
F = And(F, Not(And(Not(P), Q)))
solve(F)
F = And(F, Not(And(P, Q)))
solve(F)
# The output will obtained all the 3 possible solutions:
[P = True, Q = False]
[P = False, Q = True]
[P = True, Q = True]
no solutionPart B: SAT And Validity
# valid(P) <==> unsat(~P)
F = Implies(Not(Not(P)), P)
solve(Not(F))
# print "no solution"Part C: The DPLL algorithm
'''
nnf(P): to convert the proposition P into negation normal form;
cnf(P): to convert the proposition P into conjunction normal form;
dpll(P): to calculate the satisfiability P of the proposition P;
'''
dpll(P){
if(P==T)
return sat;
if(P==F)
return unsat;
unitProp(P); // unit prop and simplify P
x = select_atomic(P); // choose an atomic prop
if(dpll(P[x|->T])) // splitting
return sat;
return dpll(P[x|->F]);
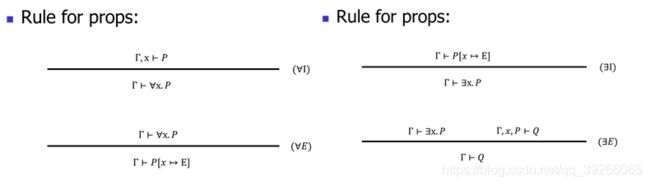
}5.谓词逻辑 Predicate logic
(一阶逻辑、FOL)
5.1 Motivcation
5.2 语法 syntax
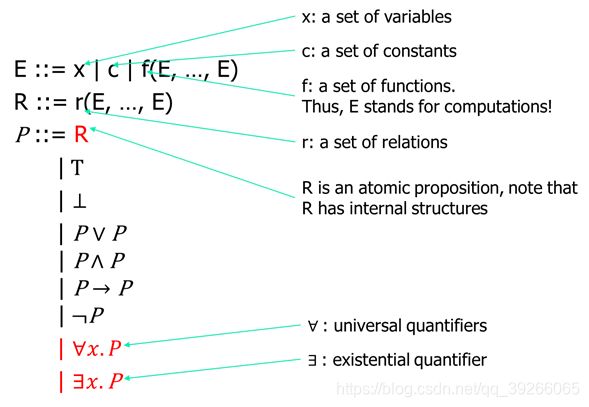
a.Bound and free variables
对于 ∀.(, )
其中x为bound var,y为free var。
把自由变量看作全局变量或外部变量。
将替换看作函数调用。
b.Substitution: P[x↦E]
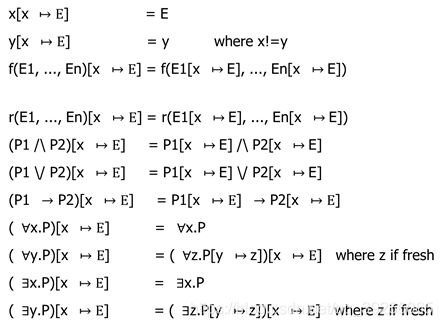
c.−renaming
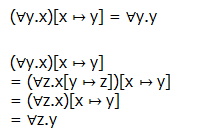
5.3 the proof theory
Judgment: Γ⊢
在命题逻辑中,Γ为一组逻辑命题,而在一阶逻辑中,Γ是一组逻辑命题或变量。
Example: P, Q, R, x, y, z ⊢
∀ 是多态的基础,∃是ADT的基础。(了解)
5.4 语义 Semantics
可靠性与完备性依然成立!可计算=可证,可证=可计算(计算机上可计算,不可判定为T还是F)。
(第五课 SAT范式、解析、DPLL算法)
6.等式和未解释函数理论
6.1Motivation
SAT对于命题逻辑,NPC问题,但是已经高效,DPLL。
对于谓词逻辑,是不可判定的,不可能有计算机算法解决,不过将其限制到一个子集中:theory,可能是可解的。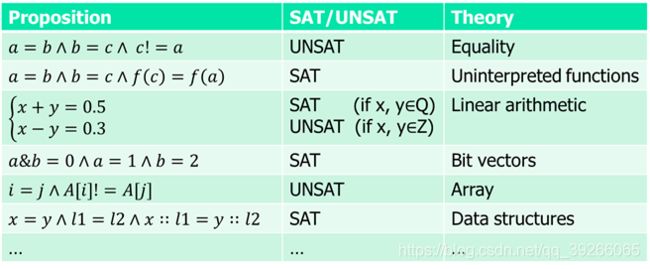
6.2 Equality and Uninterpreted Functions (EUF)
6.3 uninterpreted functions
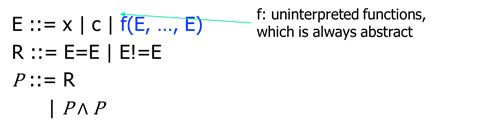
当函数符号相等,且函数符号接收的参数在对应位置上相等,才称为全等。
6.4 EUF theory applications
Assignment 5: Theory of EUF
Part A: Basic EUF theory
solve(e == f(e))
#[e = S!val!0, f = [else -> S!val!0]]
# e取值为0,f中无论取何值结果都为你0
solve(e == f(g(e, e)))
#[e = S!val!1, g = [else -> S!val!0], f = [else -> S!val!1]]
# e取值为0,f中无论取何值结果都为你0,g的结果可以为任意值
# the example from the lecture:
x1, x2, x3, x4, x5 = Consts('x1 x2 x3 x4 x5', S)
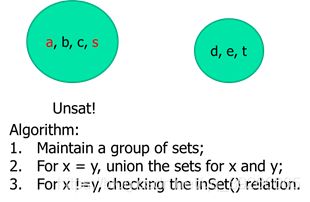
solve(x1 == x2, x2 == x3, x4 == x5, x5 != x1, f(x1) != f(x3))
# with the result "no solution".
#在S中x1=x2=x3,x4=x5,x5!=x1,但x1=x3,即f(x1)=f(x3),与约束条件矛盾。
# we can change the disequality to equality:
solve(x1 == x2, x2 == x3, x4 == x5, x5 != x1, f(x1) == f(x3))Part B: Translation validation
'''
input(source language) ---> compiler translation ---> output(target language)
| |
------------------------> translation validator <--------
'''
7.线性算数
7.1 语义
语义比较重要!一定要特别熟悉!

在有理数领域:多项式时间;
在整型Z域内:NPC。
7.2 Fourier-Motzkin variable elimination
Algorithm
1)Normalize to (only ≥0 );
2)找到变量,即存在正系数也存在负系数,即为消去后选;
3)正系数负系数两两相加消去xi;
4)消去化简后继续 1)步,此时不包含xi。
(第六次课 LA)
时间复杂度
对于n个变量,m个约束:
每一步都可能引出 m 2 / 4 m^2 / 4 m2/4个不等式,共有 m 2 n / 4 n m^{2^n}/4^n m2n/4n个。因此对于较大的n和m该算法是低效的,但是小规模的问题依然很好。
7.3 Simplex
1)Normal forms:n个等式 + n个不等式

其中 x 称为基本变量(原本存在),s称为附加变量。
例如:

2)Tableau

将自变量写在行上,将因变量写在列上,因变量随着自变量的变换而变化,并且因变量可能是对自变量存在约束。
问题:是否可以找到x、y使得s1、s2、s3满足约束?
3)Trial and fix
首先进行尝试,若不满足条件则换轴(pivoting)。
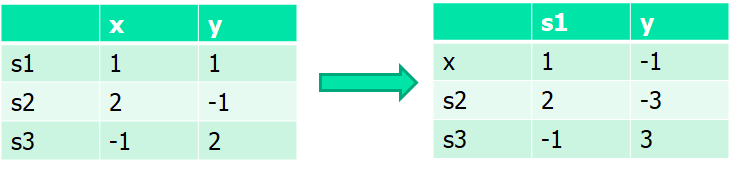
假设初值:x=y=0,则1=0, 2=0, 3=0不满足。因此换轴!
s 1 = x + y ; → x = s 1 − y ; s1 = x+y; \to x = s1-y; s1=x+y;→x=s1−y;
s 2 = 2 x − y = 2 ( s 1 − y ) − y = 2 s 1 – 3 y s2 = 2x-y = 2(s1-y)-y = 2s1 – 3y s2=2x−y=2(s1−y)−y=2s1–3y
s 3 = − x + 2 y = − ( s 1 − y ) + 2 y = − s 1 + 3 y s3 = -x+2y = -(s1-y)+2y = -s1+3y s3=−x+2y=−(s1−y)+2y=−s1+3y
此时的s1便不能随意取值,要满足其约束。
7.4 Branch & Bound (ILP)
和LP很相似,但是被限制在整型Z域。该问题是一个NPC问题,但可以用分治法解决。

7.5 LA theory applications
#1: Compiler optimization
#2: n-queens puzzle
#3: subset sum problem
#4: task scheduling
#5: task assignment
Assignment 6: Linear arithmetic
fourier_motzkin
# 1) Select a variable xi, and change the constraints into normal form,
# with m positive and n negative occurrences of xi:
#
# xi + P1(x) >= 0
# ...
# xi + Pm(x) >= 0
# -xi + Q1(x) >= 0
# ...
# -xi + Qn(x) >= 0
# R(x) >= 0
#
# 2) Eliminate xi. The previous m + n constraints will be replaced with
# m * n new constraints.
#
# P1(x) + Q1(x) >= 0
# ...
# P1(x) + Qn(x) >= 0
# P2(x) + Q1(x) >= 0
# ...
# P2(x) + Qn(x) >= 0
# ...
# Pm(x) + Qn(x) >= 0
# R(x) >= 0
#
# 3) If there're multiple variables in a single constraint, repeat step 1) and 2).simplex
(第七次课 Bit Vectors)
8.Bit Vectors
比特向量:1)数据结构 2)建模/性质推理
bug原因:
int mid = (low+high)/2;
如何解决?
int mid = low +(high+low)/2 ? ×
t0 = (x&y)+((x^y)>>1)
t = t0+(LShR(t0,31)&(x^y))![]()
L长度的比特向量b,是连续的0和1, b 0 b_0 b0是最低位,l是一个常数。
8.1Bit vectors: the syntax
8.2Semantics: arithmetic operations

Example:
<11001000>U = 200
<11001000>S = -56 (补码)
x, y = BitVecs(‘x y’, 8)
solve(x+y == 1024)
# why Z3 output:[x=0, y=0] ?
# x,y为长度为8的bitvec,x+y同理,故1024(100,0000,0000)=0(0000,0000)8.3 决策过程 Decision procedures
8.4 Incremental Bit Blasting
8.5 Bit-vectors applications
#1: Fermat‘s last theorem
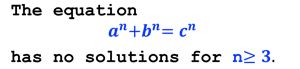

为什么要a&magic == 0???
a&magic == 0控制了a、b、c只能 2 4 = 16 2^4=16 24=16bit,在a×a×a的时候会达到48bit<64bit,否则将会溢出!
Question: why we don’t just use integers?
中止!Z3不会去遍历所有整数,因为它是无限的!所以要限定范围!
(第八次课 Arrays)
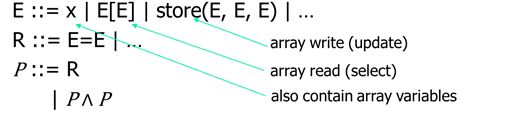
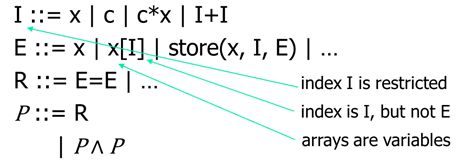
9.Arrays
9.1 Motivation

A’[k]==A[k] (k!=i,j) 代表除了变换位置i,j,其他位置的元素都不会发生改变。
函数式编程两个特性:
1.数据结构不可变化,不能修改
2.支持等式的推理,例如每次调用f(x)得到的结果都等于a。
和命令式函数不同,命令式函数中返回void,直接在原有的数据结构进行改变,而函数时式编程因为是不可写的,则每次都返回一个新构造的数组,在数组推理中,证明器总会把命令程序先转换成函数式程序,对命令式程序的推理则转换成了等价的对函数式程序的推理。
9.2 the syntax
9.3 Array Elimination
1)独立研究 2)消去和转换


Problems
一般来说,对于高阶的结果是不可判定的!但是在某种限制下还是可解的。
9.4 the restricted syntax
Array property
描述了推理Array数组相关性质时,能够出现的逻辑命题的形式是什么。
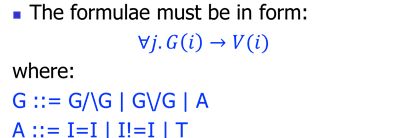
Array reduction algorithm
路线图:给出一个数组和理论,里面设计到两个关键操作:读和写,利用转换和消去的机制,把数组读改成函数调用,把数组写改成一个嵌套的store表达式,然后通过把他们翻译到EUF类型理论,得到他的求解算法。
// Goal:given a proposition in array property
// form,turn it into an EUF formulae.
// Input:any proposition P
// Output:a EUF proposition
EUF arrayReduction(P){
P1 = eliminate all
array write: store(A, i, x);
P2 = replace ∃x.P1(x) with P1(y); // y is fresh
P3 =replace ∀x.P2(x) with P2(i)/\.../\P2
P4 = eliminate array read in P3: A[i];
return P4
}9.5 Theory of Hash Tables
最后,为什么要研究数组运算?
1)在计算机中,如果有整型向量和array可以推理任何程序;
2)数组从接口上看也具有特殊性,数组的读写代表read/write、select/updata、look up\insert,代表了符号表查找表一系列结构。
例如对于Array和Hash tables:
// Array:
read(A, i);
store(A, i, x);
// Hash tables:
lookup(H, k);
update(H, k, v);在Array中i为整型,而在Hash中,k为任何一个可比较的类型。
(第九次课 Pointer)
10. Pointer programs
10.1 Motivation: pointers
指针 / 引用 / 代数数据
// subtle bug #1: dangling reference:
int *p, *q; *p = 88;
// subtle bug #2: pointer alias
p = q;
free(q);
*p = 88;
// subtle bug #3: double free
p = q;
free(p);
free(q);10.2 内存模型
平坦的、无限的内存模型:
1)按字节寻址;
2)每个对象都是固定的有限的长度;
3)地址0是不可访问的;
4)指针指的是内存地址
(数学抽象)内存模型包括存储S和堆H:
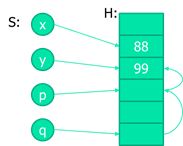
S: x → a x \to a x→a,把变量名字x映射到地址a;
H: a → v a \to v a→v,把一个地址a映射到一个值v;
10.3 Syntax & semantics
Syntax
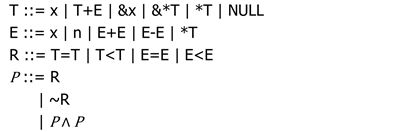
semantics
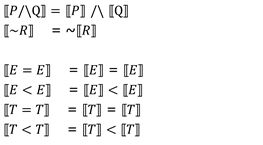
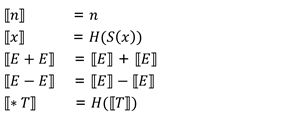
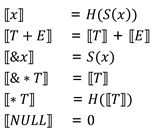
Example
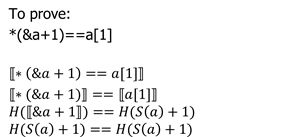
其中H,S并没有明确的定义,又转换成了未解释函数EUF问题。
10.4 A decision procedure
基于语义函数的一个决策过程!弱化和消去路线。
使用函数S和H对问题进行一个转化,也没有直接对问题进行求解。
如果一个变量的地址没有被取过或被地址化,那么就把这个变量称为纯变量,否则这个变量就被称为逃逸变量。
如果是逃逸变量,则必须存储在栈上, 必须需要有一个地址才能被取。而纯变量比较自由,既可以在栈上也可以在寄存器中。
我们可以引出内的内存模型R(x):
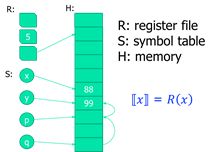
例如如下改变:
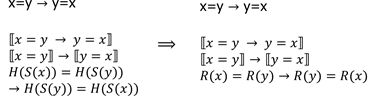
我们可以利用局部性原理,将内存切分为若干个小的内存,按照类型分类。
Key observation: for these var declarations:
int *p;
int **q;Can p and q be alias? That is, can they point to the same memory address?
The answer is NO.(recall we don’t have type conversion!)
因此我们可以得出结论:即便是同样的程序,也可以抽象出不同的模型,不同的模型就会导致对同一个命题证明会非常容易或非常复杂。
在上例中,p!=q,如果自动化去做就是程序分析中的指针分析。
核心思想:通过给出指针,构造合适的模型,可以将指针程序转换成并不含有指针的程序,从而根据已有的理论(例如EUF)建立一个对指针的算法和理论,即上文提到的第二种方法:转换和消去。
example:p=&a ∧ a=1 → *p=1
⟦=&∧=1→ ∗=1⟧
⟦=&∧=1⟧→⟦∗=1⟧
⟦=&⟧∧⟦=1⟧→⟦∗=1⟧
(H(S(p))==S(a))/\(H(S(a))==1)->(H(H(S(p)))==1) # ()=()∧(())=1→(())=1 (课件错误)
(—— 来自tiancaidong的投稿)(第十次课 理论组合)
11.Theory Combination
11.1 theories and signatures
从本质上来说,一阶逻辑是不可判定的,没有算法对他任意命题的求解,所以便选取一阶逻辑的子集,对子集进行求解,子集即理论。
在这个子集中能表达计算机的一些问题,而且可以找到一些计算机算法能够对子集有效地求解。并且其解释的确定的,即给定一个语法,可以解释到具体的规则上。

理论组合从本质上分为两大类:
1)把每一个理论都分别转换为命题逻辑的公式,然后直接用SAT方法求解。
2)每个理论分别用其特有的算法进行求解,在求解的过程中两边进行协作,信息互相传播,最终达到稳定状态即解。
10.2 Nelson-Oppen Method
如何能保证组合之后可解呢?
1)各自都是可解的
2)相交的语法为空(等号除外)
3) 无限的、稳定的(无限多个元素)
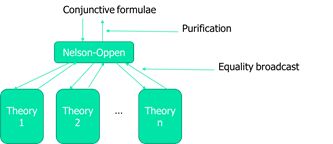
首先要明确输入与输出!其中输入一定要是合取公式(即∩),其中命题可能是混合在一块的,纯化之后依然满足合取式且为原子形式,且每个命题只属于一种理论,最后将每个理论分别丢进求解器中,然后返回等式结果,然后经过等式的传播不停反复一直到求解结束。
注意合取公式和合取范式的区别!!!
合取范式中,每个Pn还可能有内部结构,而在合取公式中必须是原子的。
10.3 Convexity 凸性

从上面的例子中可以看出,纯化后并没有等式,在LA和EUF中无法进行传播,故无法求解。
因此引入凸理论,所谓的凸理论意思就是,如果P能推出一个析取的等式,P一定能推出其中某一个。
因此需要对nelson改进:

在纯化后得到x=1或x=2之后需要进行状态分裂(split),将其中一个命题广播到x=1,另一个x=2,然后分别对EUF求解。
Soundness and completeness
对于完备性,即如果nelson返回为SAT则一定是满足的。当返回UNSAT时,是不可满足的,但是这种情况很难证明,可能是求解器不行!
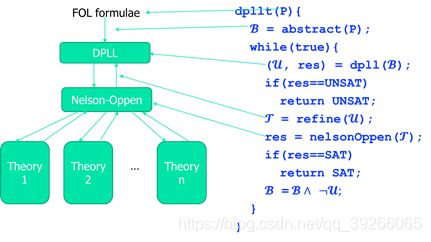
11.DPLL(T)
T表示theory,本质上还是要研究DPLL算法,即SAT算法,但这个算法是以理论T作为参数。类比为在写C++时的泛型或模板算法。
在Nelson算法中,是研究一个可满足问题,但是必须是一个合取式,但是实际上都是一般形式,就需要通过DPLL(T)求解!
一阶逻辑 → \to →抽象 → \to → 命题逻辑 → \to → 传给DPLL → \to →聚象 → \to → Nelson
抽象前后的可满足性结果可能不同,因为信息量减少!
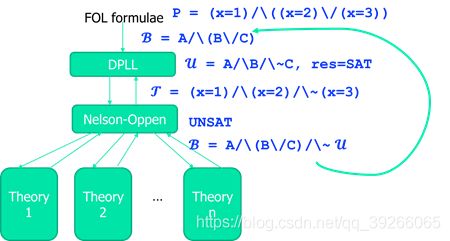
这种解法一般称为离线的,主要特点是把SAT solver用成一个黑盒,每调用一次都可以得到一个值。
注意:当nelson验证并不成立时,应当把该次DPLL计算的u完全取否后加入到下一次DPLL验证中,例如此次只是证明了如果B成立的条件下C不成立,但是并不能说明C本身不成立!
第三部分 应用
(第十一次课 Operational semantics)
12.Operational semantics
1)语义学
2)语言
12.1 A very small language: C–
bop ::= + | - | * | / | == | != | > | < | >= | …
E ::= n | x | E bop E //整型\常量\二元运算
S ::= skip //空语句
| x=E //赋值语句
| S;S //顺序语句
| f(E1, …, En) //函数调用
| if(E, S, S) //条件语句
| while(E, S) //循环语句
F ::= f(x1, …, xn){
S; return E;}Operational semantics:
- store
Store maps variables to their values::→
两种操作:更新 [⊢],读取 () - Judgment
⊢→′
在下,A化简为′。即存储器用来存放变量,A为正在研究的某一类语法符号。描述了每一类化简形式。
12.2 Operational semantics styles
Big-step operation semantics:⊢⟹
对表达式的计算是一步到位,例如复合结构,忽略内部结构,一步得到结果。
Small-step operation semantics:⊢→′
和大步结构相反,每次只计算一步!
在小步结构中,必须要走一步,因此并不存在0步,即不存在(E - n)的情况。
12.3 Operational semantics rules
在每一步中,⊢S→S’,’,因为在执行S之后,S必然发生了变换,其中可能会存在赋值,导致存储器也发生更新。
总结:这种操作语义一般被称为解释器,也叫做具体执行。(建议看看阅读材料加深理解)
(第十二次课 )
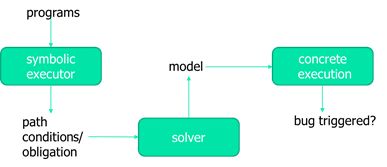
13.Symbolic execution
1)软件安全领域
2)软件测试
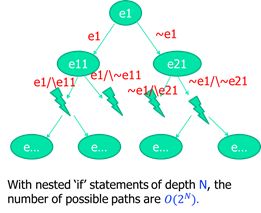
13.2 Practical Issues with Symbolic Execution
-
2.Loops and recursions
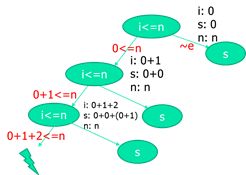
在符号执行中,并不是具体的值,因此循环并不会结束!
解决办法:有界符号执行,限制循环次数,也限制了路径的全覆盖。(循环有限化处理) -
3.Heap modeling
a)建立一个完全的符号堆,太重量级。
b)利用arrays或者pointers理论 -
4.Environment modeling
符号执行必须对环境进行建模,对所有的库的输入和输出都进行建模?
结合具体执行! -
5.constraint solving
(第十三次课 Concolic execution)
14.Concolic execution
Concolic = Concrete + symbolic
14.1 Steps
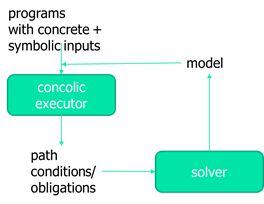
a)对一个待测试的程序,同时生成两种待测试的输入,一组是具体输入(随机取数),另一种符号数。
b)用生成的两种输入运行当前被测试的程序,同时维护两种状态。
c)如果有分支语句(条件判断),生成路径条件,但并不像符号执行中生成两种路径条件,并不产生分支。因为可通过具体值来判断哪一种是可行的路径。
d)得到路径条件之后,进行取反给求解器,得到其他的具体输入。
e)跳到b)重复执行。
![]()
在混合执行中,如果遇到上图中问题,当对 m = x × x × x m=x×x×x m=x×x×x无法求解时,需要带入x的具体值送给z3。
即不知道如何求解或不知道库函数性质时,将符号值弱化成具体值。
14.2 Advantages of Concolic Execution
a)Path explosion
每次得到一条路径,进行循环,是可控的。但是失去了路径的全覆盖。
b)Loops and recursions
混合执行时维护两个状态,是具有具体值的。
c)Environment modeling
当不知道库函数性质时,直接将具体值带入,没有符号值就将其弱化成具体的数。
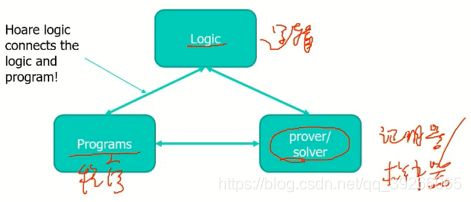
15.Hoare logic
15.1 Hoare Triple 霍尔三元组
{} {}
其中P,Q是两个逻辑命题,前提条件(pre-condition)和后条件(post-condition)。S即程序的语句。
在执行语句S之前,相关变量满足P的约束,经过S执行中止之后应当满足Q的约束。未要求执行是否中止,只是要求了程序的部分正确性。
[] []
另一种完全正确性,初始状态要满足P,并且程序S一定会终止,然后中止后满足Q。活跃性性质。
15.2 Proposition syntax
15.3 Proposition semantics
⊨
代表存储器(内存),P在store 上成立,即用存储器上的值取代命题P上的变量,结果P成立。
∀.∀′.(⊨ ∧ ⊢⟹′) → ′⊨
对于任意的在P上成立,并且在下S执行得到’,依然成立,便可以推出Q在’上成立。
15.4 Axiomatic semantics
定义一套公理系统来做推理。建立一个可靠性和完备性理论。
⊨{}{} ⟺ ⊢{}{}
15.5 inference rules
a)empty 空语句,在执行之后状态不变。
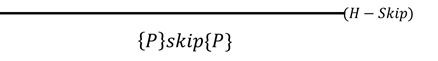
b)assignment 赋值语句 将P中的x替换成E

c)sequence 顺序(序列)
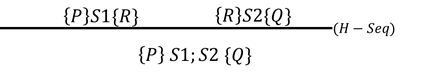
d)if
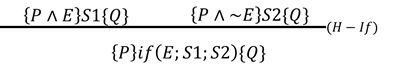
e)while
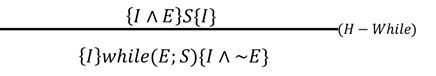
f)consequence (唯一一个不是语法制导)
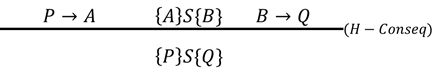
(第十四次课 Verification condition)
16. Verification condition
霍尔逻辑的本质是一个推理系统,利用其定理和推理规则。构造一棵证明树!
对于一个霍尔三元组:{} {}
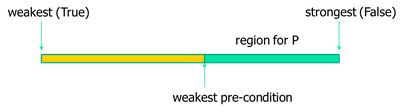
给定一个执行S,通过条件Q来计算一个A,假设A执行S后满足Q,A是一个最弱的前提条件。
那么只需要证明对于任意的P,→即可。
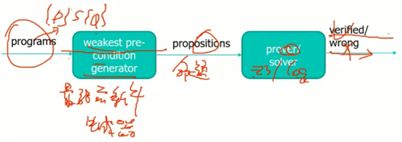
16.1 Weakest pre-condition generation
根据霍尔三元组,S,Q计算一个最弱前提条件生成。还是对执行S的归纳,即语法制导(syntax-directed)。
a)empty
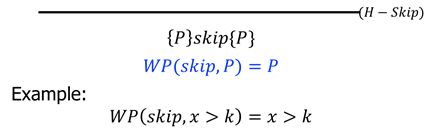
b)assignment
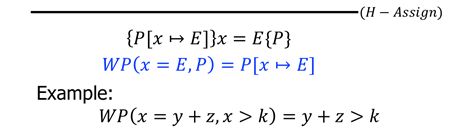
c)sequence

d)if
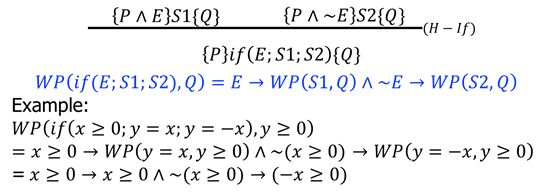
e)while

16.2 Verification Condition
最弱前提条件是不可行计算的,于是讨论验证条件!
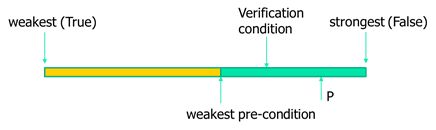
1)验证条件比最弱前提条件好求解;
2)依然比用户给定的前提条件弱!程序永远比程序员更懂程序!
最核心的洞察就是循环,循环不中止!每写一个循环都要标识一个循环不变式。
w h i l e I ( E ; S ) {while}_I(E;S) whileI(E;S) , I I I就是循环不变式!一般不要求,但是要让循环可行的话就需要给出循环不变式。
有了循环不变式之后就可以构造一个验证条件生成器:

最核心的部分就是生成器算法:
// Induction on syntactic form of a statement S;
// backward computation:
//语法制导
VC(skip, P) = P //在这种情况下,最弱前提条件=验证条件
VC(S1;S2, P) = VC(S1, VC(S2, P))
VC(x=e, P) = P[x↦e]
VC(if(e;s1;s2), P) = (e→VC(s1, P))∧(~e → VC(s2, P))
VC(whileI(e;s), P) = I∧(∀ ⃗.I →(e → VC(s, I) ∧(~e → P)))
//循环不变式在进入循环前就要成立,且循环不管经过多少次退出时依然成立,循环中也要成立16.3 VC爆炸的问题
对一个问题分析:
1)可能不存在算法
2)存在算法,但复杂度很高
3)需要存储量较大(VC爆炸)

16.4 Forward calculation of Verification Conditions
关键思想:符号执行!