[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)
该系列文章是讲解Python OpenCV图像处理知识,前期主要讲解图像入门、OpenCV基础用法,中期讲解图像处理的各种算法,包括图像锐化算子、图像增强技术、图像分割等,后期结合深度学习研究图像识别、图像分类应用。希望文章对您有所帮助,如果有不足之处,还请海涵~
前面一篇文章介绍了直方图统计,包括Matplotlib和OpenCV绘制直方图、掩膜直方图、灰度直方图对比及通过直方图预测黑夜白天。这篇文章将详细讲解图像增强知识,从而改善图像质量,增强图像识别效果,核心内容分为直方图均衡化、局部直方图均衡化和自动色彩均衡三部分。万字长文整理,希望对您有所帮助。 同时,该部分知识均为作者查阅资料撰写总结,并且开设成了收费专栏,为小宝赚点奶粉钱,感谢您的抬爱。当然如果您是在读学生或经济拮据,可以私聊我给你每篇文章开白名单,或者转发原文给你,更希望您能进步,一起加油喔~
代码下载地址(如果喜欢记得star):
- https://github.com/eastmountyxz/ImageProcessing-Python
文章目录
- 一.图像增强概述
-
- 1.空间域
- 2.频率域
- 二.直方图均衡化
-
- 1.原理知识
- 2.举例分析原理
- 3.代码实现
- 三.局部直方图均衡化
- 四.自动色彩均衡化
- 五.总结
前文参考:
- [Python图像处理] 一.图像处理基础知识及OpenCV入门函数
- [Python图像处理] 二.OpenCV+Numpy库读取与修改像素
- [Python图像处理] 三.获取图像属性、兴趣ROI区域及通道处理
- [Python图像处理] 四.图像平滑之均值滤波、方框滤波、高斯滤波及中值滤波
- [Python图像处理] 五.图像融合、加法运算及图像类型转换
- [Python图像处理] 六.图像缩放、图像旋转、图像翻转与图像平移
- [Python图像处理] 七.图像阈值化处理及算法对比
- [Python图像处理] 八.图像腐蚀与图像膨胀
- [Python图像处理] 九.形态学之图像开运算、闭运算、梯度运算
- [Python图像处理] 十.形态学之图像顶帽运算和黑帽运算
- [Python图像处理] 十一.灰度直方图概念及OpenCV绘制直方图
- [Python图像处理] 十二.图像几何变换之图像仿射变换、图像透视变换和图像校正
- [Python图像处理] 十三.基于灰度三维图的图像顶帽运算和黑帽运算
- [Python图像处理] 十四.基于OpenCV和像素处理的图像灰度化处理
- [Python图像处理] 十五.图像的灰度线性变换
- [Python图像处理] 十六.图像的灰度非线性变换之对数变换、伽马变换
- [Python图像处理] 十七.图像锐化与边缘检测之Roberts算子、Prewitt算子、Sobel算子和Laplacian算子
- [Python图像处理] 十八.图像锐化与边缘检测之Scharr算子、Canny算子和LOG算子
- [Python图像处理] 十九.图像分割之基于K-Means聚类的区域分割
- [Python图像处理] 二十.图像量化处理和采样处理及局部马赛克特效
- [Python图像处理] 二十一.图像金字塔之图像向下取样和向上取样
- [Python图像处理] 二十二.Python图像傅里叶变换原理及实现
- [Python图像处理] 二十三.傅里叶变换之高通滤波和低通滤波
- [Python图像处理] 二十四.图像特效处理之毛玻璃、浮雕和油漆特效
- [Python图像处理] 二十五.图像特效处理之素描、怀旧、光照、流年以及滤镜特效
- [Python图像处理] 二十六.图像分类原理及基于KNN、朴素贝叶斯算法的图像分类案例
- [Python图像处理] 二十七.OpenGL入门及绘制基本图形(一)
- [Python图像处理] 二十八.OpenCV快速实现人脸检测及视频中的人脸
- [Python图像处理] 二十九.MoviePy视频编辑库实现抖音短视频剪切合并操作
- [Python图像处理] 三十.图像量化及采样处理万字详细总结(推荐)
- [Python图像处理] 三十一.图像点运算处理两万字详细总结(灰度化处理、阈值化处理)
- [Python图像处理] 三十二.傅里叶变换(图像去噪)与霍夫变换(特征识别)万字详细总结
- [Python图像处理] 三十三.图像各种特效处理及原理万字详解(毛玻璃、浮雕、素描、怀旧、流年、滤镜等)
- [Python图像处理] 三十四.数字图像处理基础与几何图形绘制万字详解(推荐)
- [Python图像处理] 三十五.OpenCV图像处理入门、算数逻辑运算与图像融合(推荐)
- [Python图像处理] 三十六.OpenCV图像几何变换万字详解(平移缩放旋转、镜像仿射透视)
- [Python图像处理] 三十七.OpenCV和Matplotlib绘制直方图万字详解(掩膜直方图、H-S直方图、黑夜白天判断)
- [Python图像处理] 三十八.OpenCV图像增强万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)
图像增强是将原来不清晰的图像变清晰或强调某些兴趣特征,扩大图像中不同物体特征之间的差别,抑制不感兴趣的特征,改善图像质量,丰富图像信息,从而加强图像的识别和处理,满足某些特殊分析的需要。本文主要讲解图像增强的基础概念,重点阐述直方图均衡化处理及彩色直方图均衡化处理,后续第39篇博客和第40篇博客将详细讲解图像平滑和图像锐化处理。
一.图像增强概述
图像增强(Image Enhancement)是指按照某种特定的需求,突出图像中有用的信息,去除或者削弱无用的信息。图像增强的目的是使处理后的图像更适合人眼的视觉特性或易于机器识别。 在医学成像、遥感成像、人物摄影等领域,图像增强技术都有着广泛的应用。图像增强同时可以作为目标识别、目标跟踪、特征点匹配、图像融合、超分辨率重构等图像处理算法的预处理算法。
由于很多在高动态范围场景、昏暗环境或特殊光线条件下拍摄的图像视觉效果不佳,需要进行后期增强处理压缩或拉伸动态范围或提取一致色感才能满足显示和印刷的要求。图1所示是需要进行增强处理的图像的举例。
- 图1(a)为一幅在高动态范围的场景中拍摄的照片,图中左上角天空区域亮度很高,但右侧大半边的树所在区域却很暗,细节几乎不可见,需采用色调映射方法进行增强,以压缩动态范围增强暗处细节。
- 图1(b)为一幅在水下拍摄的图像,整体动态范围很低,细节辨识不清,全图都需要进行对比度增强。
图像增强通常划分为如图2所示的分类,其中最重要的是图像平滑和图像锐化处理,分别于第39篇博客和第40篇博客介绍
图像增强按其变换处理所在的作用域不同而被分为空间域方法和频率域方法两大类。而由于具体的应用目的不同,其图像实际增强处理所用到的方法和增强的内容有一定的差异,但图像增强处理的各目标和方法并不互相排斥,某些应用中需要同时联合几种方法来实现最好的增强效果。
1.空间域
空间域增强通常包含:
- 图像灰度级变换
- 图像直方变换
- 直方均衡
- 使用模糊逻辑和基于优化的增强算法
如使用遗传算法和细菌觅食等算法进行优化处理以达到图像增强的目的。空间域图像增强方法的一般定义如公式(1)。其中,f(x,y) 为输入的待增强的图像,g(x,y) 为处理后的增强图像,T为空间域变换函数,表示对原图像在像素空间所进行的各种变换操作。当T操作定义在单个像素点 (x,y) 上时,称该操作为点操作;而空间滤波指T操作作用于像素点 (x,y) 的邻域上时的相应处理。
![]()
空间域增强方法按处理策略的差异,又可分为:
- 全局一致性处理
该方法较为简单,仅对图像空间像素值进行统一的调整,则未考虑像素点在空间中的分布特性。 - 局部自适应处理
该法较复杂,主要针对图像局部对比度、边缘等特殊区域信息进行增强。
直方图均衡
它是图像增强处理中对比度变换调整中最典型的方法。该方法是空域增强中最常用、最简单有效的方法之一,其采用灰度统计特征,将原始图像中的灰度直方图从较为集中的某个灰度区间转变为均匀分布于整个灰度区域范围的变换方法。通常又划分为:
- 全局直方图均衡
该方法的主要优点是算法简单、速度快,可自动增强图像;全局直方图均衡方法的缺点是对噪声敏感、细节信息易失,在某些结果区域产生过增强问题,且对对比度增强的力度相对较低。 - 局部直方图均衡
该方法的主要优点是局部自适应,可最大限度的增强图像细节;其缺点是增强图像质量操控困难,并会随之引入噪声。
2.频率域
基于频域的图像增强算法基础为卷积理论,该方法把图像视为波,然后利用信号处理手段来处理图像。其通用的数学表示如下公式(2)所示。
![]()
由上式逆变换后,产生增强后的图像 g(x,y),其表达如下公式(3)所示:
其中,g(x,y) 为增强后的图像,F(x,y) 为原图像的傅立叶变换,H(x,y) 为滤波变换函数,通过大量的实验研究,发现增强处理后的图像具有比原图像更加清晰的细节。常用的滤波方法有低通、高通、带阻及同态滤波等。
频域图像增强方法从本质上是一种间接对图像进行变换处理的方法,其最早的变换理论,由傅立叶的《热分析理论》指出的周期函数表达可由不同频率和不同倍乘系数表达的正/余弦和形式表征。随着图像处理应用不断发展,频率域变换方法近年来在小波变换基础上发展了具有更高精度和更好稀疏表达特性的方法,更加适合于表达图像的边缘轮廓信息,如 Curvelet 和 Contourlet 变换。这些超小波变换都是基于变换域的新型的多尺度分析方法,在图像对比度增强、降噪、图像融合与分割等方面得到了广泛地应用。
二.直方图均衡化
1.原理知识
直方图均衡化是图像灰度变化的一个重要处理,被广泛应用于图像增强领域。它是指通过某种灰度映射将原始图像的像素点均匀地分布在每一个灰度级上,其结果将产生一幅灰度级分布概率均衡的图像。 直方图均衡化的中心思想是把原始图像的灰度直方图从比较集中的某个灰度区间转变为全范围均匀分布的灰度区间,通过该处理,增加了像素灰度值的动态范围,从而达到增强图像整体对比度的效果。直方图均衡化包括三个核心步骤:
- 统计直方图中每个灰度级出现的次数;
- 计算累计归一化直方图;
- 重新计算像素点的像素值。
直方图均衡化示意图如图3所示,左边的像素值集中于中心部分,通过均衡化处理后,图像峰值不再这么高,同时0-50、200-255灰度值部分存在像素值。简单理解就是将图像的灰度值进行拉伸。
图4将左边像素偏暗的原始图像进行直方图均衡化处理,得到右边的图像色彩更均衡。
直方图均衡化算法的详细处理过程如下:
(1) 计算原始图像直方图的概率密度。
计算过程如公式(3)所示,其中, r k r_k rk 表示第k个灰度级(k=0,1,2,…,L-1),L最大值为256; n k n_k nk 表示图像中灰度级为rk的像素个数;N表示图像中像素的总个数; P ( r k ) P(r_k) P(rk) 为图像中第k个灰度级占总像素数的比例。
(2) 通过灰度变换函数T计算新图像灰度级的概率密度。
新图像灰度级的概率密度是原始图像灰度级概率密度的累积,如公式(4)所示。其中,k是新图像的灰度级,k=0,1,2,…,L-1;表示原始图像的第k个灰度级;为直方图均衡化处理后的第k个灰度级。
(3) 最后计算新图像的灰度值。
由于公式(4)计算所得的sk位于0至1之间,需要乘以图像的最大灰度级L,转换为最终的灰度值res,如公式(5)所示。
图5(a)表示原始图像,图5(b)表示其对应的直方图,x轴表示256个灰度级,y轴表示各个灰度级出现的频数。
图6(a)表示直方图均衡化处理后的图像,图6(b)表示其对应的直方图。从效果图可以看出,经过直方图均衡化处理,图像变得更加清晰,图像的灰度级分布也更加均匀。
2.举例分析原理
下面举一个简单的例子说明直方图均衡化的算法流程。假设存在如公式(6)所示的7×7个像素点的图像。
(1) 通过各像素值出现的次数,其统计结果如表1所示,其中像素值0出现了9次,像素值1出现了9次,依次类推,像素值7出现了8次。
(2) 接着将表1的结果进行归一化处理,即当前像素值出现的次数除以总的像素个数(总个数为49),比如像素值0的归一化结果为0.18,像素值1的归一化结果为0.18,依次类推,像素值7的归一化结果为0.16。
(3) 然后统计各像素值的累计直方图,比如像素值0的累计直方图百分比为0.18,像素值1的累计直方图百分比为像素值0(百分比为0.184)加上像素值1(百分比为0.184),最终结果四舍五入为0.37,依次类推,像素值7的累计直方图百分比为1.00。
(4) 最后将各像素值的累计直方图百分比乘以像素范围的最大值,此处的范围为0到7,故乘以最大值7,得到一个新的结果,即为直方图均衡化处理的结果,如表4所示。
表4将原始像素级的8个结果(0、1、2、3、4、5、6、7)直方图均衡化为6个新的结果(1、3、4、5、6、7),生成如图7所示的直方图。
其中图7(a)是原始图像各像素级的直方图,图7(b)是直方图均衡化处理后的各像素级的直方图,最终结果更加均衡。直方图均衡化可以让色彩细节更丰富,获取更多的信息,常用于人脸识别、车牌识别、医疗图像处理等领域。
3.代码实现
Python调用OpenCV中的cv2.equalizeHist()函数实现直方图均衡化处理,并且为全局直方图均衡化。其函数原型如下所示,输出的dst图像与输入图像src具有相同的大小和类型。
- dst = cv2.equalizeHist(src)
– src表示输入图像,即原图像
– dst表示目标图像,直方图均值化处理的结果
下面的代码是调用cv2.equalizeHist()函数实现图像直方图均衡化处理。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-03-12
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图片
img = cv2.imread('test.png')
#灰度转换
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#直方图均衡化处理
result = cv2.equalizeHist(gray)
#显示图像
cv2.imshow("Input", gray)
cv2.imshow("Result", result)
cv2.waitKey(0)
cv2.destroyAllWindows()
输出结果如图8所示,左边为原始图像,右边为直方图均衡化处理图像,它有效提升了图像的亮度及细节。
下面代码调用函数ravel()绘制了对应的直方图,并进行直方图均衡化处理前后的图像对比。
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-03-12
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图片
img = cv2.imread('lena.bmp')
#灰度转换
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#直方图均衡化处理
result = cv2.equalizeHist(gray)
#显示图像
plt.subplot(221)
plt.imshow(gray, cmap=plt.cm.gray), plt.axis("off"), plt.title('(a)')
plt.subplot(222)
plt.imshow(result, cmap=plt.cm.gray), plt.axis("off"), plt.title('(b)')
plt.subplot(223)
plt.hist(img.ravel(), 256), plt.title('(c)')
plt.subplot(224)
plt.hist(result.ravel(), 256), plt.title('(d)')
plt.show()
输出结果如图9所示,图9(a)为原始图像,对应的直方图为图9©,图9(b)和图9(d)为直方图处理后的图像及对应直方图,它让图像的灰度值分布更加均衡。
如果需要对彩色图片进行全局直方图均衡化处理,则需要分解RGB三色通道,分别进行处理后再进行通道合并。完整代码如下所示:
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-03-12
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图片
img = cv2.imread('yxz.jpg')
# 彩色图像均衡化 需要分解通道 对每一个通道均衡化
(b, g, r) = cv2.split(img)
bH = cv2.equalizeHist(b)
gH = cv2.equalizeHist(g)
rH = cv2.equalizeHist(r)
# 合并每一个通道
result = cv2.merge((bH, gH, rH))
cv2.imshow("Input", img)
cv2.imshow("Result", result)
#等待显示
cv2.waitKey(0)
cv2.destroyAllWindows()
#绘制直方图
plt.figure("Hist")
#蓝色分量
plt.hist(bH.ravel(), bins=256, normed=1, facecolor='b', edgecolor='b')
#绿色分量
plt.hist(gH.ravel(), bins=256, normed=1, facecolor='g', edgecolor='g')
#红色分量
plt.hist(rH.ravel(), bins=256, normed=1, facecolor='r', edgecolor='r')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
输出结果如图10所示,左边为彩色原始图像,右边为直方图均衡化处理图像,它有效提升了图像的亮度及细节。
对应的直方图如图11所示,其中x轴表示图像的灰度级,y轴表示各灰度级所对应的直方图。
三.局部直方图均衡化
前面第二小节通过调用OpenCV中equalizeHist()函数实现直方图均衡化处理,该方法简单高效,但其实它是一种全局意义上的均衡化处理,很多时候这种操作不是很好,会把某些不该调整的部分给均衡处理了。同时,图像中不同的区域灰度分布相差甚远,对它们使用同一种变换常常产生不理想的效果,实际应用中,常常需要增强图像的某些局部区域的细节。
为了解决这类问题,Pizer等提出了局部直方图均衡化的方法(AHE),但AHE方法仅仅考虑了局部区域的像素,忽略了图像其他区域的像素,且对于图像中相似区域具有过度放大噪声的缺点。为此K. Zuiderveld等人提出了对比度受限CLAHE的图像增强方法,通过限制局部直方图的高度来限制局部对比度的增强幅度,从而限制噪声的放大及局部对比度的过增强,该方法常用于图像增强,也可以被用来进行图像去雾操作。CLAHE和AHE的区别在于前者对区域对比度进行了限制,且采用插值来加快计算。
在OpenCV中,调用函数createCLAHE()实现对比度受限的局部直方图均衡化。它将整个图像分成许多小块(比如按10×10作为一个小块),那么对每个小块进行均衡化。这种方法主要对于图像直方图不是那么单一的(比如存在多峰情况)图像比较实用。其函数原型如下所示:
- ==retval = createCLAHE([, clipLimit[, tileGridSize]]) ==
– clipLimit参数表示对比度的大小
– tileGridSize参数表示每次处理块的大小
调用createCLAHE()实现对比度受限的局部直方图均衡化的代码如下:
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-03-12
import cv2
import numpy as np
import matplotlib.pyplot as plt
#读取图片
img = cv2.imread('lena.bmp')
#灰度转换
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
#局部直方图均衡化处理
clahe = cv2.createCLAHE(clipLimit=2, tileGridSize=(10,10))
#将灰度图像和局部直方图相关联, 把直方图均衡化应用到灰度图
result = clahe.apply(gray)
#显示图像
plt.subplot(221)
plt.imshow(gray, cmap=plt.cm.gray), plt.axis("off"), plt.title('(a)')
plt.subplot(222)
plt.imshow(result, cmap=plt.cm.gray), plt.axis("off"), plt.title('(b)')
plt.subplot(223)
plt.hist(img.ravel(), 256), plt.title('(c)')
plt.subplot(224)
plt.hist(result.ravel(), 256), plt.title('(d)')
plt.show()
输出结果如图12所示,图12(a)为原始图像,对应的直方图为图12©,图12(b)和图12(d)为对比度受限的局部直方图均衡化处理后的图像及对应直方图,它让图像的灰度值分布更加均衡。可以看到,相对于全局的直方图均衡化,这个局部的均衡化似乎得到的效果更自然一点。
四.自动色彩均衡化
Retinex算法是代表性的图像增强算法,它根据人的视网膜和大脑皮层模拟对物体颜色的波长光线反射能力而形成,对复杂环境下的一维条码具有一定范围内的动态压缩,对图像边缘有着一定自适应的增强。
自动色彩均衡(Automatic Color Enhancement,ACE) 算法是在Retinex算法的理论上提出的,它通过计算图像目标像素点和周围像素点的明暗程度及其关系来对最终的像素值进行校正,实现图像的对比度调整,产生类似人体视网膜的色彩恒常性和亮度恒常性的均衡,具有很好的图像增强效果。ACE算法包括两个步骤:
- 一是对图像进行色彩和空域调整,完成图像的色差校正,得到空域重构图像;
- 二是对校正后的图像进行动态扩展。
ACE算法计算公式如下:
其中,W是权重参数,离中心点像素越远的W值越小;g是相对对比度调节参数,其计算方法如公式(9)所示,a表示控制参数,该值越大细节增强越明显。
![]()
图13是条形码图像进行ACE图像增强后的效果图,通过图像增强后的图13(b)对比度更强,改善了原图像的明暗程度,增强的同时保持了图像的真实性。
由于OpenCV中暂时没有ACE算法包,下面的代码是借鉴“zmshy2128”老师的文章,修改实现的彩色直方图均衡化处理[8]。后面有机会作者详细分析其代码实现过程。
- 自动色彩均衡(ACE)快速算法 - zmshy2128老师
# -*- coding: utf-8 -*-
# By:Eastmount CSDN 2021-03-12
# 参考zmshy2128老师文章
import cv2
import numpy as np
import math
import matplotlib.pyplot as plt
#线性拉伸处理
#去掉最大最小0.5%的像素值 线性拉伸至[0,1]
def stretchImage(data, s=0.005, bins = 2000):
ht = np.histogram(data, bins);
d = np.cumsum(ht[0])/float(data.size)
lmin = 0; lmax=bins-1
while lmin<bins:
if d[lmin]>=s:
break
lmin+=1
while lmax>=0:
if d[lmax]<=1-s:
break
lmax-=1
return np.clip((data-ht[1][lmin])/(ht[1][lmax]-ht[1][lmin]), 0,1)
#根据半径计算权重参数矩阵
g_para = {
}
def getPara(radius = 5):
global g_para
m = g_para.get(radius, None)
if m is not None:
return m
size = radius*2+1
m = np.zeros((size, size))
for h in range(-radius, radius+1):
for w in range(-radius, radius+1):
if h==0 and w==0:
continue
m[radius+h, radius+w] = 1.0/math.sqrt(h**2+w**2)
m /= m.sum()
g_para[radius] = m
return m
#常规的ACE实现
def zmIce(I, ratio=4, radius=300):
para = getPara(radius)
height,width = I.shape
#Python3报错如下 使用列表append修改
"""
#TypeError: can only concatenate list (not "range") to list
#增加max
print(range(height),type(range(height)))
print([0]*radius,type([0]*radius))
print([height-1]*radius,type([height-1]*radius))
zh = [0]*radius + max(range(height)) + [height-1]*radius
zw = [0]*radius + max(range(width)) + [width -1]*radius
#[0,0,0] + [0,1,2,3] + [3,3,3]
#[0, 0, 0, 0, 1, 2, 3, 3, 3, 3]
"""
zh = []
zw = []
n = 0
while n < radius:
zh.append(0)
zw.append(0)
n += 1
for n in range(height):
zh.append(n)
for n in range(width):
zw.append(n)
n = 0
while n < radius:
zh.append(height-1)
zw.append(width-1)
n += 1
#print(zh)
#print(zw)
Z = I[np.ix_(zh, zw)]
res = np.zeros(I.shape)
for h in range(radius*2+1):
for w in range(radius*2+1):
if para[h][w] == 0:
continue
res += (para[h][w] * np.clip((I-Z[h:h+height, w:w+width])*ratio, -1, 1))
return res
#单通道ACE快速增强实现
def zmIceFast(I, ratio, radius):
print(I)
height, width = I.shape[:2]
if min(height, width) <=2:
return np.zeros(I.shape)+0.5
Rs = cv2.resize(I, (int((width+1)/2), int((height+1)/2)))
Rf = zmIceFast(Rs, ratio, radius) #递归调用
Rf = cv2.resize(Rf, (width, height))
Rs = cv2.resize(Rs, (width, height))
return Rf+zmIce(I,ratio, radius)-zmIce(Rs,ratio,radius)
#rgb三通道分别增强 ratio是对比度增强因子 radius是卷积模板半径
def zmIceColor(I, ratio=4, radius=3):
res = np.zeros(I.shape)
for k in range(3):
res[:,:,k] = stretchImage(zmIceFast(I[:,:,k], ratio, radius))
return res
#主函数
if __name__ == '__main__':
img = cv2.imread('test02.png')
res = zmIceColor(img/255.0)*255
cv2.imwrite('Ice.jpg', res)
运行结果如图14和图15所示,ACE算法能有效进行图像去雾处理,实现图像的细节增强。
最后秀一把女神的去雾效果,可惜失真了,哈哈,继续加油!
五.总结
写到这里,本文就介绍完毕。这篇文章主要讲解图像增强的基础概念,并详细讲解了全局直方图均衡化、局部直方图均衡化和自动色彩均衡化算法,结合实际案例进行分析。这些算法可以广泛应用于图像增强、图像去噪、图像去雾等领域。
-
一.图像增强概述
1.空间域
2.频率域 -
二.直方图均衡化
1.原理知识
2.举例分析原理
3.代码实现 -
三.局部直方图均衡化
-
四.自动色彩均衡化
-
源代码下载地址,记得帮忙点star和关注喔。
https://github.com/eastmountyxz/ImageProcessing-Python
时光嘀嗒嘀嗒的流失,这是我在CSDN写下的第八篇年终总结,比以往时候来的更早一些。《敏而多思,宁静致远》,仅以此篇纪念这风雨兼程的一年,这感恩的一年。转眼小宝白天了,哈哈~提前祝大家新年快乐!
- 2020年总结:敏而多思,宁静致远——纪念这风雨兼程的一年
2020年8月18新开的“娜璋AI安全之家”,主要围绕Python大数据分析、网络空间安全、人工智能、Web渗透及攻防技术进行讲解,同时分享CCF、SCI、南核北核论文的算法实现。娜璋之家会更加系统,并重构作者的所有文章,从零讲解Python和安全,写了近十年文章,真心想把自己所学所感所做分享出来,还请各位多多指教,真诚邀请您的关注!谢谢。
![]()
(By:Eastmount 2021-03-12 晚上12点 http://blog.csdn.net/eastmount/ )
参考文献,在此感谢这些大佬,共勉!
- [1] 罗子江, 杨秀璋. Python中的图像处理[M]. 2020.
- [2]冈萨雷斯. 数字图像处理(第3版)[M]. 北京:电子工业出版社, 2013.
- [3]张恒博, 欧宗瑛. 一种基于色彩和灰度直方图的图像检索方法[J]. 计算机工程, 2004.
- [4]Eastmount. [数字图像处理] 四.MFC对话框绘制灰度直方图[EB/OL]. (2015-05-31). https://blog.csdn.net/eastmount/article/details/46237463.
- [5]王浩,张叶,沈宏海,张景忠.图像增强算法综述[J].中国光学,2017,10(04):438-448.
- [6]许欣. 图像增强若干理论方法与应用研究[D].南京理工大学,2010.
- [7]李艳梅. 图像增强的相关技术及应用研究[D].电子科技大学,2013.
- [8]阮秋琦. 数字图像处理学(第3版)[M]. 北京:电子工业出版社, 2008.
- [9] S. Bidon, Olivier Besson, J. Y. Tourneret. The Adaptive Coherence Estimator is the Generalized Likelihood Ratio Test for a Class of Heterogeneous Environments[J]. IEEE Signal Processing Letters, 2008, 15: 281-284.
- [10]zmshy2128. 自动色彩均衡(ACE)快速算法[EB/OL]. (2016-12-05). https://www.cnblogs.com/zmshy2128/p/6135551.html.
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第1张图片](http://img.e-com-net.com/image/info8/7ce40e3193f149eb8e769e471129fa51.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第2张图片](http://img.e-com-net.com/image/info8/8e9d40c01b694ab0af8adefceae69ce0.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第3张图片](http://img.e-com-net.com/image/info8/65abfbf7337648a096732424a56e09b4.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第4张图片](http://img.e-com-net.com/image/info8/38b7b870c3f94a49afc30032697ad7e9.jpg)
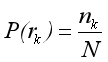

![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第5张图片](http://img.e-com-net.com/image/info8/d2db7dd4f3d341d5b31f3b34b66749c9.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第6张图片](http://img.e-com-net.com/image/info8/1642cce7b59f497d9a0e35c6440745ac.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第7张图片](http://img.e-com-net.com/image/info8/0287e46372e04b638a96a0fbe180855d.png)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第8张图片](http://img.e-com-net.com/image/info8/5f9f3176ee9e4b1e93f3f6aec3376fcf.png)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第9张图片](http://img.e-com-net.com/image/info8/d126523e888f468db2c22c8dd4e2bfb2.png)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第10张图片](http://img.e-com-net.com/image/info8/376e874bdd084738aa709390d518bcc1.png)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第11张图片](http://img.e-com-net.com/image/info8/8c6a65116b384b44a04345cbefcb927b.png)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第12张图片](http://img.e-com-net.com/image/info8/39df087af07342afb10e8a7055c59933.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第13张图片](http://img.e-com-net.com/image/info8/a7740138c2dc49bcaa562f71e4edac31.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第14张图片](http://img.e-com-net.com/image/info8/fb843016f6604390b305e222c3d6c769.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第15张图片](http://img.e-com-net.com/image/info8/306675d75a4f47e2b275f7d1444cb375.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第16张图片](http://img.e-com-net.com/image/info8/f32647906b154b4eb8aaaac1bf1d0134.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第17张图片](http://img.e-com-net.com/image/info8/afbba9f2df604a219d228605f770bcff.jpg)

![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第18张图片](http://img.e-com-net.com/image/info8/a3f31a9fca6048a2afd8947cb9e638ce.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第19张图片](http://img.e-com-net.com/image/info8/aac6b15ba3cf44349f1856ea5e8e55e8.jpg)
![[Python图像处理] 三十八.OpenCV图像增强和图像去雾万字详解(直方图均衡化、局部直方图均衡化、自动色彩均衡化)_第20张图片](http://img.e-com-net.com/image/info8/2841e35de0284f3f94a4130c486230c7.jpg)