随机森林

1.概述

1.1 集成算法概述

集成学习通过在数据上构建多个模型，集成所有模型的建模结果，汇总之后得到一个综合的结果，以此来获取比单个模型更好的回归或分类表现。

多个模型集成成为的模型叫做“集成评估器”，组成集成评估器的每个单个的模型叫做“基评估器”。

1.2 集成算法分类

装袋法(Bagging)：装袋法的核心是构建多个相互独立的基评估器，然后对各个基评估器的预测结果进行平均或按照少数服从多数的方式来决定集成评估器的结果，装代法的代表就是随机森林

提升法(Boosting)：在提升法中，基评估器是按顺序——构建的，其核心思想是结合弱评估器的力量一次次对难以评估的样本进行预测，从而得到一个强评估器。提升法的代表模型有Adaboost和梯度提升树。

2.随机森林搭建

2.1 随机森林分类器(RandomForestClassifier)

sklearn.ensemble.RandomForestClassifier(n_estimators='10',criterion='gini',max_depth=None,min_samples_split=2,min_samples_leaf=1,min_features,min_impurity_decrease)

2.1.1 重要参数解读

参数	含义
criterion	不纯度的衡量指标，有基尼系数和信息熵两种选择
max_depth	数的最大深度，超过最大深度的树枝都会被剪掉
min_samples_leaf	一个节点在分支后的每个子节点都必须包含至少min_samples_leaf个训练样本，否则就不会被分支
min_samples_split	一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝，否则就不会发生
max_features	max_features限制分枝时考虑的特征个数，超过限制个数的特征都会被舍弃，默认值为总特征个数开平方
min_impurity_decrease	限制信息增益的大小，信息增益小于设定数值的分枝就不会发生

2.1.2 搭建随机森林分类器

（1）导入相关的库

%matplotlib inline
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import cross_val_score
from matplotlib.pyplot as plt

（2）导入需要的数据集

wine = load_wine()
wine.data       # 查看 wine 的特征值
wine.target     # 查看 wine 的标签值

（3）建立决策树和随机森林模型

from sklearn.model_selection import train_test_split

X_train,Xtest,ytrain,ytest = train_test_split(wine.data,wine.target,test_size=0.3)
clf = DecisionTreeClassifier(random_state=0)
rfc = RandomForestClassifier(random_state=0)
clf = clf.fit(X_train,ytrain)
rfc = rfc.fit(X_train,ytrain)
score_c = clf.score(Xtest,ytest)
score_r = rfc.score(Xtest,ytest)

print('Single tree:{}'.format(score_c)
     ,'Random Forest:{}'.format(score_r))

  Single tree:0.9074074074074074     Random Forest:0.9444444444444444

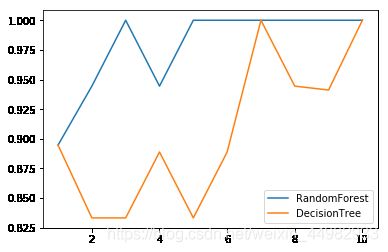
（4）画出随机森林和决策树在一组交叉验证下的效果对比

label = 'RandomForest'
for model in [RandomForestClassifier(n_estimators=25),DecisionTreeClassifier()]:
    score = cross_val_score(model,wine.data,wine.target,cv=10)
    print('{}:'.format(label)),print(score.mean())
    plt.plot(range(1,11),score,label=label)
    plt.legend()
    label = 'DecisionTree'

RandomForest:
0.9783625730994153
DecisionTree:
0.9058135534915721

随机森林和决策树在一组交叉验证下的效果对比

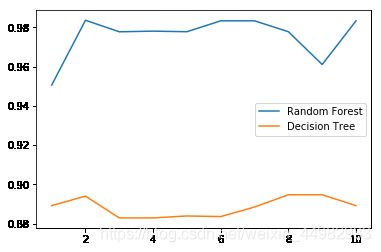
（5）画出随机森林和决策树在十组交叉验证下的效果对比

rfc_1 = []
clf_1 = []

for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    rfc_1.append(rfc_s)
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf,wine.data,wine.target,cv=10).mean()
    clf_1.append(clf_s)

plt.plot(range(1,11),rfc_1,label='Random Forest')
plt.plot(range(1,11),clf_1,label='Decision Tree')
plt.legend()
plt.show()

随机森林和决策树在十组交叉验证下的效果对比

从4,5两步不难看出，单个决策树的波动轨迹和随机森林在大体上是保持一致的，单个决策树的准确率越高，随机森林的准确率也就越高

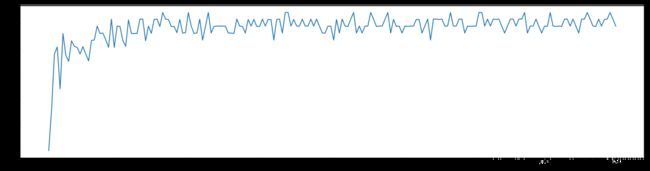
（6）n_estimators 的学习曲线

superpa = []
for i in range(1,201):
    rfc = RandomForestClassifier(n_estimators=i)
    rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10).mean()
    superpa.append(rfc_s)
print(max(superpa),superpa.index(max(superpa)))
plt.figure(figsize=(20,5))
plt.plot(range(1,201),superpa)
plt.show()

0.9888888888888889 40

随机森林学习曲线

由上图可以看出，随机森林的预测准确率并不会随着基评估器的增多而不算上升，而是==在基评估器的数量达到一定的数目时，准确率进行来回的波动

2.2 随机森林准确率为什么优于决策树

随机森林本质上是一种袋装法集成算法，袋装法集成算法对基评估器的预测结果进行平均或用多数表决的原则来决定集成评估器的结果，在刚才的红酒例子中，我们建立了25棵树，对任何一个样本而言，平均或多数表决原则下，当且仅当有13棵以上的树判断错误时，随机森林才会判断错误，单独一棵决策树对红酒数据集的分类准确率在0.89上下浮动，假设一棵树判断错误的可能性为0.2，那20棵树判断错误的可能性为：

其中是判断错误的次数，也是判断错误的树的数量，是一棵树判断错误的概率，是判断正确的概率，共判对次

import numpy as np
from scipy.special import comb
np.array([comb(25,i)*(0.2**i)*(1-0.2)**(25-i) for i in range(13,26)]).sum()

0.00036904803455582827

可见，随机森林判断错误的几率非常小，这让随机森林在红酒数据集上的表现远远好于单棵决策树

2.3bootstrap & oob_score

袋装法通过又放回的随机抽样技术来形成不同的训练数据，进而生成数目众多的基分类器，即决策分类树，bootstrap就是用来控制抽样技术的参数。

bootstrap通过对含有n个样本的原始训练集中有放回的抽取n次，形成一个规模大小与原样本大小一致的自助集。由于是随机采样，这样每次生成的自助集和原始数据集不同，和其他的采样集也不同，这样我们就可以自由创造取之不尽用之不竭，并且互不相同的自助集，用这些自助集来训练我们的基分类器，基分类器自然也不相同

bootstrap参数默认为True，代表采用这种有放回的随机抽样技术

但是放回抽样会存在样本无法被完全抽到的问题，即自助集大约会含有63%的原始数据，因为，每一个样本被抽到的某个自助集的概率为：

当足够大时，这个概率收敛于
因此，会有约37%数据会被浪费掉，因此在随机森林中，我们可以不用划分训练集和测试集，可以使用袋内数据进行训练，使用袋外数据进行测试

# 无需划分训练集和测试集
rfc = RandomForestClassifier(n_estimators=40,random_state=0,oob_score=True)
rfc = rfc.fit(wine.data,wine.target)
# 重要属性oob_score_
rfc.oob_score_

0.9831460674157303

在实例化时将oob_score这个参数调整为True，训练完成之后我们就可以通过oob_score_来查看我们的袋外数据的测试结果

2.4 随机森林的重要属性和接口

属性名称	属性功能
estimators_	查看随机森林里各个基分类器，即单个树的具体情况
oob_score_	查看袋外数据的测试结果
feature_importances_	查看各个特征在模型学习中的重要性程度

接口名称	接口功能
score	返回测试样本的模型预测准确度
predict	返回每个测试样本的分类/回归结果
predict_proba	返回每个测试样本被分到各个类的概率（此接口只适用于随机森林分类器）
apply	返回每个测试样本所在的叶子节点的索引此接口只适用于随机森林分类器）

2.5 随机森林回归器(RandomForestClassifier)

sklearn.ensemble.RandomForestRegressor(n_estimators='warn',criterion='mse',max_depth=None,min_samples_split=2,min_samples_leaf=1,min_features,min_impurity_decrease)

随机森林回归器和随机森林分类器参数与属性基本相同，不再做过多的阐述，要注意的是在随机森林回归器中的cross_val_score中的scoring如果不设置为neg_mean_squared_error则交叉验证默认的衡量指标为r2

3.使用随机森林填补缺失值

3.1 原理阐述

回归算法认为，特征矩阵和标签之间存在着某种关系，所以通过特征矩阵可以推倒出标签值，同样知道标签值也可以倒推出特征矩阵，随机森林填补缺失值的理念便是基于此

对于一个有n个特征的数据来说，如果特征T有缺失值，我们就把T当做标签，其他的n-1个特征和原本的标签组成新的特征矩阵。那对于T来说，它没有缺失的部分就是我们的Y_train，这部分数据既有标签也有特征，而它缺失的部分，只有特征没有标签，就是我们需要预测的部分

3.2 代码实操

（1）导入需要的库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.impute import SimpleImputer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score

（2）以波士顿数据集为例，导入完整的数据集进行探索

dataset = load_boston()

dataset.data.shape
#总共506*13=6578个数据

X_full,y_full = dataset.data,dataset.target
n_samples = X_full.shape[0]
n_features = X_full.shape[1]

（3）为完整的数据集放入缺失值

#首先确认放入缺失值的比例，假设为50%，那么就是要放入6578*0.5=3289个数据

rng = np.random.RandomState(0)  # 生成随机数种子
missing_rate = 0.5
n_missing_samples = int(np.floor(n_samples*n_features*missing_rate))
#np.floor 向下取整，返回.0的浮点数，利用int将其变为整数

'''接着创建3289个我们要创建缺失值的索引
   创建一个数组，包含3289个分布在0~506中间的行索引，和3289个分布在0~13之间的列索引,
   这样我们就可以利用索引来为数据中的任意3289个位置赋空值'''

missing_samples = np.random.randint(0,n_samples,n_missing_samples)
missing_features = np.random.randint(0,n_features,n_missing_samples)

'''我们现在采集了3289个样本数据，远远超过我们所需要的样本量506，所以我们使用随机抽取的函数randint。但是如果我们需要的数据量
   小于我们的样本量506,我们可以使用np.random.choice来抽样，choice会随机抽取不重复的随机数，因此可以帮助我们让数据更加分散'''
#missing_samples = np.random.choice(dataset.data.shape[0],n_missing_samples,replace=False)

X_missing = X_full.copy()
y_missing = y_full.copy()
#利用X_missing和y_missing替代X_full和y_full防止对原有数据集进行破坏
X_missing[missing_samples,missing_features] = np.nan

X_missing = pd.DataFrame(X_missing)

（4）利用随机森林填补缺失值

X_missing_reg = X_missing.copy()
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values

for i in sortindex:
    #构建我们的新特征矩阵和新标签
    df = X_missing_reg
    fillc = df.iloc[:,i]
    df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
    #在新特征矩阵中，对含有缺失值的列，进行0的填补
    df_0 =SimpleImputer(missing_values=np.nan,
                        strategy='constant',fill_value=0).fit_transform(df)
    #找出我们的训练集和测试集
    Ytrain = fillc[fillc.notnull()]
    Ytest = fillc[fillc.isnull()]
    Xtrain = df_0[Ytrain.index,:]
    Xtest = df_0[Ytest.index,:]
    #用随机森林回归来填补缺失值
    rfc = RandomForestRegressor(n_estimators=100)
    rfc = rfc.fit(Xtrain, Ytrain)
    Ypredict = rfc.predict(Xtest)
    #将填补好的特征返回到我们的原始的特征矩阵中
    X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = Ypredict

（5）对填补好的数据进行建模

X = [X_full,imp_mean,imp_0,X_missing_reg]

mse = []
for x in X:
    estimator = RandomForestRegressor(random_state=0,n_estimators=100)
    scores = cross_val_score(estimator,x,y_full,scoring='neg_mean_squared_error',cv=10).mean()
    mse.append(scores*-1)    

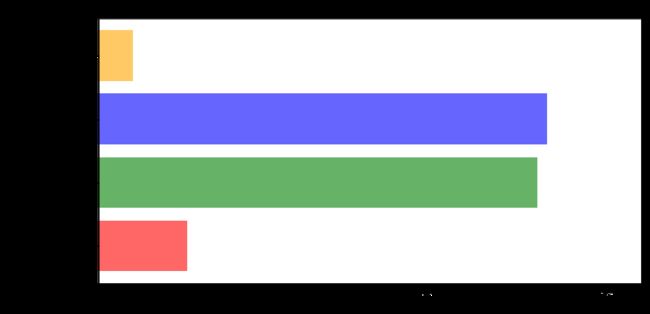
（6）用所得结果画出条形图

x_labels = ['Full data','Zero Imputation','Mean Imputation','Regressor Imputation']
colors = ['r','g','b','orange']

plt.figure(figsize=(12,6))
ax = plt.subplot(111)
for i in np.arange(len(mse)):
    ax.barh(i,mse[i],color=colors[i],alpha=0.6,align='center')
ax.set_title('Imputation Techniques with Boston Data')
ax.set_xlim(left=np.min(mse)*0.9,right=np.min(mse)*2.5)
ax.set_yticks(np.arange(len(mse)))
ax.set_xlabel('MSE')
ax.set_yticklabels(x_labels)
plt.show()

Imputation Techniques with Boston Data

由上图可以看出，用随机森林对缺失值填充之后模型获得了更小的均方误差，准确性得到了提高，比用均值和0填充缺失值好了很多

4.随机森林调参基本思想

4.1 泛化误差

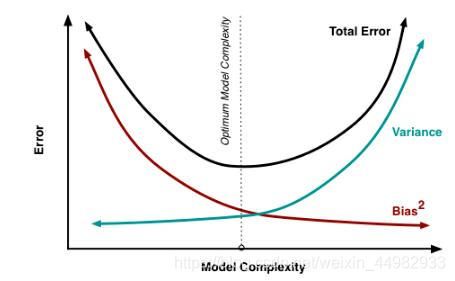
泛化误差是衡量模型在未知数据上的准确率的指标，当模型在位置数据上表现糟糕时，我们说模型的泛化程度不够，泛化误差大，模型的效果就会不好，泛化误差受到模型复杂度的影响，当模型太复杂，模型就会过拟合，泛化能力就会不好，所以泛化误差大，当模型太简单，模型就会欠拟合，拟合能力不够，所以误差也会增大，如下图所示

泛化误差与模型复杂度关系图

对树模型和树的集成模型来说，树的深度越深，枝叶越多，模型越复杂，树模型和树的集成模型的目标，都是减少模型的复杂度，把模型往图像的左边移动，我们可以依据下标参数的重要性程度，对参数进行调节，尽量避免网格搜索

参数	含义	影响程度
n_estimators	n_estimators值越大，模型越复杂	★★★★
max_depth	有增有减，默认最大深度，向复杂度降低的方向调参，max_depth，模型更简单，图像向左移动	★★★
min_samples_leaf	有增有减，默认限制为1，即最高复杂度，向复杂度降低的方向调参，min_samples_leaf，模型更简单，图像向左移动	★★
min_samples_split	有增有减，默认限制为2，即最高复杂度，向复杂度降低的方向调参，min_samples_split，模型更简单，图像向左移动	★★
max_features	有增有减，默认是auto，是特征总数开平方，位于中间复杂度，既可以向复杂度升高的方向，也可以向复杂度降低的方向调参max_features，模型更简单，图像右移，max_features，模型更复杂，图像左移	★
criterion	有增有减，一般是gini

4.2 示例：随机森林在乳腺癌数据上的调参

（1）导入相关的库文件

from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

（2）导入数据集，探索数据

data = load_breast_cancer()
data.data.shape
data.target.shape

（3）进行一次简答的建模，看看模型本身在数据集上的效果

rfc = RandomForestClassifier(n_estimators=100,random_state=90)
score_pre = cross_val_score(rfc,data.data,data.target,cv=10).mean()
score_pre

0.9648809523809524

（4）随机森林调参第一步：优先调试参数n_estimators

# 先画出超参数学习曲线，在大致范围上进行观察，再小范围取值调优
scorel = []
for i in range(1,201,10):
    rfc = RandomForestClassifier(n_estimators=i,random_state=90,n_jobs=-1)
    score = cross_val_score(rfc,data.data,data.target,cv=10).mean()
    scorel.append(score)
print(max(scorel),(scorel.index(max(scorel))*10))
plt.figure(figsize=[20,5])
plt.plot(range(1,201,10),scorel)
plt.show()

0.9631265664160402 70

n_estimators,0~200分布图

由上代码结果以及图片所示，随机森林的准确度在70上最大，我们可以选定65-75进行小范围调优

scorel = []
for i in range(65,75):
    rfc = RandomForestClassifier(n_estimators=i,
                                 n_jobs=-1,
                                 random_state=90)
    score = cross_val_score(rfc,data.data,data.target,cv=10).mean()
    scorel.append(score)
print(max(scorel),([*range(65,75)][scorel.index(max(scorel))]))
plt.figure(figsize=[20,5])
plt.plot(range(65,75),scorel)
plt.show()

0.9666353383458647 73

n_estimators小范围趋势图

由最终的结果可知，当 n_estimators=73时，随机森林模型的准确率达到最高，为0.9666，比没有调参前的0.9631，高出0.0032，可见参数 n_estimators对模型准确率影响之大

（5）随机森林调参第二步：调试参数max_depth
在这里我们使用网格搜索GridSearchCV的方式对max_depth进行调优，首先整理一下接下来使用网格进行调优的参数

"""
有一些参数是没有参照的，很难说清一个范围，这种情况下我们使用学习曲线，看趋势
从曲线跑出的结果中选取一个更小的区间，再跑曲线
param_grid = {'n_estimators':np.arange(0, 200, 10)}
param_grid = {'max_depth':np.arange(1, 20, 1)}  
param_grid = {'max_leaf_nodes':np.arange(25,50,1)}
对于大型数据集，可以尝试从1000来构建，先输入1000，每100个叶子一个区间，再逐渐缩小范围

有一些参数是可以找到一个范围的，或者说我们知道他们的取值和随着他们的取值，模型的整体准确率会如何变化，这
样的参数我们就可以直接跑网格搜索
param_grid = {'criterion':['gini', 'entropy']}
param_grid = {'min_samples_split':np.arange(2, 2+20, 1)}
param_grid = {'min_samples_leaf':np.arange(1, 1+10, 1)}
param_grid = {'max_features':np.arange(5,30,1)}
"""

param_grid = {'max_depth':np.arange(1,20,1)}

# 一般根据数据的大小来进行一个试探，乳腺癌数据很小，所以可以采用1~10，或者1~20这样的试探
# 但对于大型数据来说，我们应该尝试30~50层深度
# 更应该画出学习曲线，来观察深度对模型的影响
rfc = RandomForestClassifier(n_estimators=73
                             ,random_state=90
                            )
GS = GridSearchCV(rfc,param_grid,cv=10)
GS.fit(data.data,data.target)

GS.best_params_

{'max_depth': 8}

GS.best_score_

0.9666353383458647

由最终的结果可以知道，调试完max_depth之后模型的准确率并没有发生改变，其实已经可以认定，模型已经处于泛化误差曲线的最低点，没有调试的控键了，其余0.04的误差完全是由噪音数据所造成的，已经无法通过调试参数的方式再进行提升，这个时候可以采取更换模型以及数据等方式进行进一步的调优

其余网格参数调优的方法用max_depth大家可以自行尝试